利用速度的定义求解绳斜拉物体模型中的速度

刘胜功 赵汝花

（山东省阳谷县第一中学，山东 阳谷 252300）

拜读了贵刊2010年第3期刊登的《也谈交点速度问题的解法》一文，和文中提到的前面几期上刊登的相关类型问题的分析，受益匪浅.联系自己平时讲授这类问题的情况，觉得从速度的定义出发解决绳子斜拉物体或物体斜拉绳问题，是易于接受，又便于理解的快捷方法.现对这种方法作简单阐述，以与同行进行商榷.

绳子斜拉物体或物体斜拉绳的模型在高中物理中比较常见.笔者曾经讲授这类问题时，按照速度分解要根据实际效果进行分解的思想，通过分析得出：绳子斜拉物体或物体斜拉绳时，物体运动的速度是合速度，沿绳长伸长或缩短方向的速度是一个分速度，垂直于绳即绳端转动的方向的速度为另一个分速度.但是学生接受起来好像知其然不知其所以然.在后来的讲授中，笔者从理解瞬时速度的定义出发，通过一两个例题，引导学生共同分析，学生反映接受的效果较好.下面是讲授这类问题的基本思路.

按照现行人民版《物理》必修1中速度的定义：物理学中用位移与发生这个位移所用时间的比值表示物体运动的快慢，这就是速度.一般来说，物体在某一时间间隔内运动快慢不一定是一样的，所以只能理解为这是物体的平均速度.为了使描述精确些，可以把Δt取得小一些.物体在从t到t＋Δt这样一个较小的时间间隔内运动快慢的差异也就小一些.Δt越小，运动的描述就越精确，如果Δt非常小，就可以认为表示的是物体在时刻t的瞬时速度.

我们可以根据以上思路来分析绳子斜拉物体或物体斜拉绳问题.由于拉动绳子，一方面船和滑轮间的绳子变短，另一方面绳子连接物体的一端转过一个小的角度.设想物体在很短的时间Δt内发生了很短的位移，进而利用几何关系求出一个物体在Δt时间内沿实际效果方向分位移间与实际位移的关系，根据速度的定义，求出且当Δt很小时，就可认为是这两个方向的分速度.为了进一步说明此方法，下面举几个例子.

例1.如图1，人在岸上以恒定的速度v0通过滑轮用不可伸长的绳拉水中的小船，当绳与水平方向成θ角时，小船沿水面向岸靠近的速度v多大？

解析：在拉动小船的过程中，小船与滑轮间的绳子长度减小，另一方面，绳子绕滑轮转动.

图1

设在很短的时间Δt内，小船向前运动了Δx，则绳子也转过一个小角度，使得绳子与水平方向的夹角增加 了 Δθ.连 接AB 使A、B与滑轮间距离相等，船与滑轮间绳子的长度缩短了长度BC，如图2所示.

图2

例2.如图3所示，使动滑轮以速度v向上运动，当不可伸长的绳与墙成α角的瞬时，求物体速度大小.

解析：在拉动滑轮的过程中，绳子固定端与滑轮间的绳子长度增大，另一方面，绳子在绕固定端转动.

图3

设想在很短的时间Δt内，动滑轮由A位置升高到B位置，升高量为y，如图4，则滑轮到墙上固定点的距离增加量等于的长度.由数学知识＝ycosθ.由于滑轮升高量故物体共升高了y＋ycosθ.

图4

例3.如图5所示，临界角为45°液面上有一点光源S，用遮光纸遮住，只留下一束竖直向下垂直入射到水平放置于液体中且距离液面为d的平面镜M 上.当平面镜M绕垂直过中心O的轴以角速度ω逆时针匀速转动时，观察者发现水面上有一光斑掠过.设t＝0时平面镜处于水平位置且镜面向上，试确定观察者所观察到的光斑在水面上移动速度v与时间t的函数关系式.

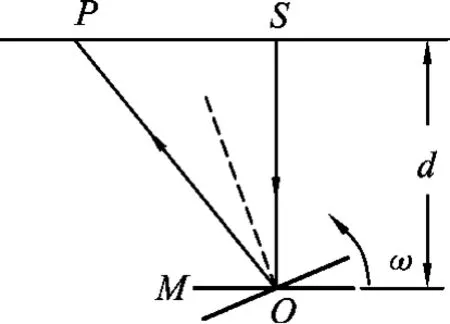
图5

解析：反射光束一方面绕O点转动，同时在水中的长度要伸长.如图6所示，设经过时间t，平面镜转过角度θ＝ωt，则反射光线和入射光线的夹角为2θ，反射光线转动的角速度为2ω，此时光线反射到水面上的P点.设经过一个很小的时间间隔Δt，平面镜又转过Δθ＝ωΔt，反射光线与入射光线的夹角增加了2Δθ＝2ωΔt，反射光束转到OQ，水面上的光斑由P点移到Q点.作OR＝OP，则QR就是在Δt内反射光束在水中增加的长度.PR为P点绕O点转过的小短弧.由于Δt很小，PR接近直线，且∠PRO近似等于90°，三角形QRP可以看作直角三角形，且∠QPR＝2θ，PR＝而在三角形OSP中所以

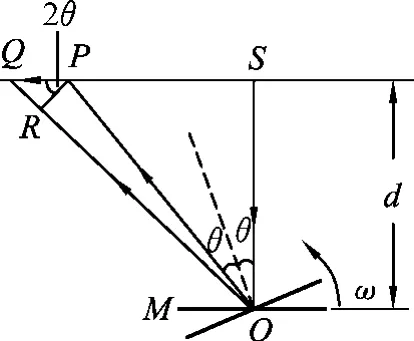
图6

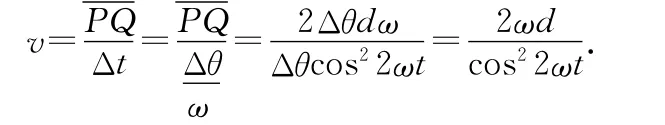
例4.如图7所示，物体M套在光滑的竖直杆上，和m通过细绳和定滑轮相连，定滑轮与杆间的距离为d，当M下落h时，速度达到vM，求此时m的速度vm.

解析：当M下落时，M与滑轮间绳子变长，同时绳子绕滑轮转动.如图8所示，设物体下落h时，绳子与杆的夹角为θ，再经过一段很短的时间Δt，M下落y，M与滑轮间绳子长度增加了x，即物体m上升的位移为x.

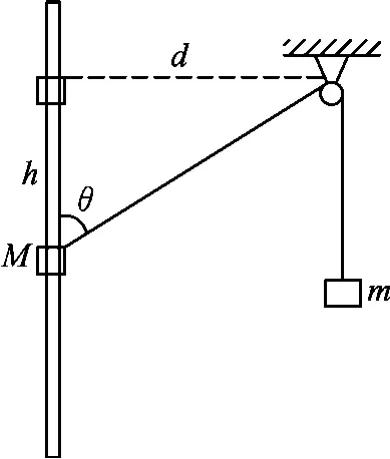
图7

图8

由于Δt很小，角θ变化也很微小，可认为vMsinθ＝vm，所以有

以上几个例题都属于绳斜拉物体模型的问题.通过例题可以看出，在根据实际问题设出一个微小时间Δt后，辅之简单的几何关系，根据速度的定义求解绳斜拉物体模型的分速度，比较易于掌握.由于是从速度的定义出发去分析求解，故可适用于一切求速度分解的问题，但在有的题目中过于强调这种方法则有繁琐之感.求解速度的分解问题，应视具体问题而定.让学生掌握这种方法，既可巩固学生对速度概念的掌握，又能提高学生发散思维能力，培养学生分析问题的基本技能.