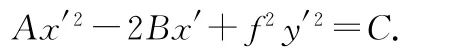物理竞赛中的椭圆

郑 金

（凌源市职教中心，辽宁 朝阳 122500）

在数学中，到两个定点的距离之和等于常数的点的集合为椭圆.当以长轴为x轴时，椭圆的标准方程为

椭圆是一种圆锥曲线，在平面上到定点F的距离与到定直线l的距离之比为常数e的点的集合是椭圆.偏心率为小于1的正数；近焦点到准线的距离即焦准距为在以椭圆的远焦点为极点，以长轴所在直线为极轴的极坐标系中，椭圆的极坐标方程为r＝若设半通径即半正焦弦为ρ0，则由定义可知ρ0因此

椭圆的光学性质：从椭圆的一个焦点发出的光线，经椭圆反射后，反射光线经过另一个焦点.由反射定律知，椭圆上任一点的法线平分该点对两个焦点的张角.即椭圆上任一点的法线平分焦点三角形的顶角.

1 力学中的椭圆

某些行星和卫星等天体在万有引力作用下的运动轨迹多为椭圆.

图1

解析：把质点的椭圆运动视为两个沿坐标轴方向的同一频率的简谐运动的叠加，设t＝0时x＝a，则y＝0，因此质点的运动方程为

分速度为vx＝－aωsinωt，vy＝bωcosωt，所以

对分速度求导数得分运动的加速度为

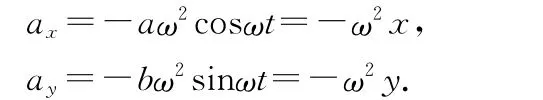
对应的回复力分别为Fx＝－mω2x，Fy＝－mω2y，设曲率半径与Fy方向夹角为θ，则合速度与vx方向夹角为θ.可知法向力为

还可利用极坐标方程求解，在图1中，在以左焦点为极点，以x轴为极轴的极坐标系中，由于左焦点为远焦点，则椭圆的极坐标方程为对于右顶点，r＝a＋c，θ＝0，所以

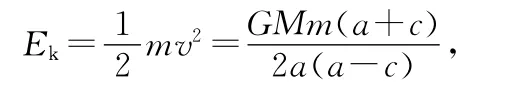
另解：在万有引力作用下，物体的机械能和角动量都守恒.由于在远地点和近地点的速度都与矢径垂直，则角动量为L＝mv·r，机械能总量为

远、近地点的矢径长度为方程的两个根，由韦达定理可知

2 热学中的椭圆

例2.（第15届全国中学生物理竞赛预赛题）1mol理想气体缓慢地经历了一个循环过程，在p－V图中这一过程是一个椭圆，如图2所示.已知此气体若处在与椭圆中心O′点所对应的状态时，其温度为T0＝300k.求在整个循环过程中气体的最高温度T1和最低温度T2各是多少？

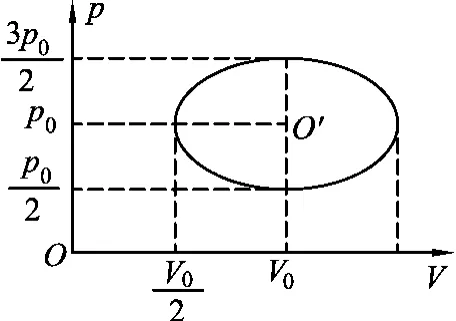
图2

与椭圆相切的等温线，所对应的温度为循环过程的最高或最低温度.

假如画图时取横纵坐标轴的刻度相等，则椭圆变为正圆，那么圆心过第一象限的角分线，而等温线与圆周的切点在角分线上，可知离原点最远的切点坐标为

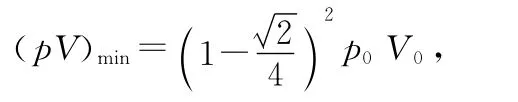
易知另一个切点即离坐标原点最近的切点的坐标为

拓展：若循环过程沿顺时针方向，则气体做功情况如何？

解析：因循环过程沿顺时针方向，则气体对外做功，数值上等于椭圆的面积，由公式S＝πab得

3 电学中的椭圆

例3.真空中有一固定点电荷，带正电为Q，另一点电荷带负电为q，质量为m，绕Q做椭圆运动，Q位于椭圆的一个焦点上，q与Q的最大距离为a，最小距离为b，如图3所示，求：（1）q绕Q运动的周期；（2）负电荷在距正电荷最近点和最远处的速率；（3）若负电荷在距正电荷最远处获得能量而绕其做圆周运动，它获得的能量是多大？

解析：（1）由于在椭圆运动过程中q只受Q的库仑引力，跟行星绕恒星做椭圆运动时所受的万有引力相似，则带电粒子的椭圆运动也遵循开普勒第三定律，即电荷q做椭圆运动周期的平方与其长半轴的3次方成正比.由题意知椭圆的半长轴为因此椭圆运动周期等于q绕Q做半径为的匀速圆周运动的周期.由得

图3

（2）由角动量守恒有mv1·b＝mv2·a，由能量守恒定律有

解得近点和远点的速率分别为

（3）设负电荷绕正电荷做半径为a的圆周运动的速度为v3，则有此时具有的动能为

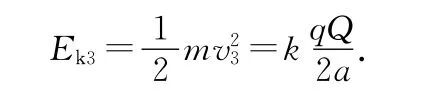
所以负电荷在远点获得的能量为

4 光学中的椭圆

例4.如图4所示，真空中的一束平行光线沿平行于长轴的方向射入折射率为n的旋转椭球体介质中，为使所有光线都严格会聚于椭圆旋转体的右焦点，试求出偏心率应满足的关系.

解析：以主轴为极轴，右焦点为极点，建立极坐标系如图5所示，极轴方向向右，从左准线开始沿主轴向右传播的一束平行光的光程可表示为

图4

已知cosθ＜0，则以近焦点为极点，以长轴所在直线为极轴的极坐标系中，极坐标方程为故

图5

由费马原理可知，光程差为定值，则后两项之和应该为定值，即

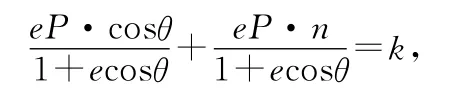
化简得ecosθ（P－k）＝k－ePn.

为使θ取任何值时等式都成立，须使cosθ的系数为零，即k＝P，所以P（1－en）＝0，解得

例5.把一个球形框架放在凸透镜的一侧，使球心位于主光轴上距光心两倍焦距处，球半径r＜f，试推断这个球形框架通过透镜所成的像的形状是球形体还是椭球体？

解析：以光心为坐标原点，主光轴为x轴，建立直角坐标系如图6所示.设圆心坐标为（c，0），则圆的方程为

图6

令A＝（f＋c）2－r2，B＝f（c2＋cf－r2），C＝f2（r2－c2），则有