雷达CFAR检测的仿真研究①

2012-07-18郝迎春陈客松

全球定位系统 2012年1期

郝迎春，陈客松

（电子科技大学电子工程学院，四川成都611731）

0 引言

在定位系统中，雷达起着关键作用。雷达定位主要测量目标的两个信息——距离和角度。有了目标相对雷达的距离信息和角度信息，就可以知道目标相对雷达的位置，从而实现定位。在雷达检测目标过程中，回波信号往往淹没在接收机热噪声或杂波中。杂波通常定义为对雷达检测无用的回波信号，如建筑物、陆地、云层、海洋等背景散射回波。在检测单元信噪比（SNR）已知的情况下，可以通过设定固定的检测门限判断是否存在目标。而在实际雷达工作环境中，信噪比（SNR）参数的缺失大大限制了固定门限检测的应用和虚警概率的控制。

CFAR技术作为一种动态门限检测算法，能够根据检测单元周围其它的杂波样本功率动态设定检测门限，在维持预定虚警概率的条件下，最大化检测概率。视频的回波信号与噪声、杂波一起送到检测器，在检测器对视频信号进行分级，即设置一个检测门限。如果信号超过该门限，就判决目标存在。显然，门限电平的选择是至关重要的。如果门限设置太高，本来可以检测的弱小目标将被丢失；如果门限设置太低，则虚警太多。因此，门限电平的设置将直接影响到雷达检测目标的能力［1－2]。对邻近单元平均恒虚警（CA－CFAR）检测算法进行了研究，通过仿真方法确定实际检测门限，并且比较了有限参考单元数情况下不同窗长时的检测性能。

1 CFAR检测算法

均值类CFAR处理方法的共同特点是在局部估计中采用了取均值的方法。假设v（t）是单脉冲检测中某个辨识单元中得到的一个观测，D（v）是由v（t）形成的检测统计量，在平方律检波的情况下，D（v）应具有如下形式

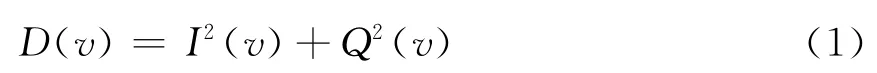
式中：I（v）和Q（v）分别为信号的同相和正交分量的匹配滤波器输出；D（v）为杂波包络；许多检测问题中，可认为杂波包络服从瑞利分布，CA－CFAR检测器结构可以用图1表示。图中，分别用xi（i＝1，…，n）和yj（j＝1，…，n）表示两侧参考单元采样；参考滑窗长度N＝2n，n为前沿和后沿参考滑窗长度；X和Y分别是前沿和后沿滑窗的局部估计，此时自适应判决准则为

其中：H1表示有目标的假设；H0表示没有目标的假设；Z为杂波功率水平估计，它就是参考滑窗中的平均包络估计；T为标称化因子；D表示检测单元中的检测统计量D（V）.与检测单元最邻近的两个保护单元主要用在单目标情况下，防止目标能量泄漏到参考单元影响检测器的两个局部估计值，但一般可不采用［3]。

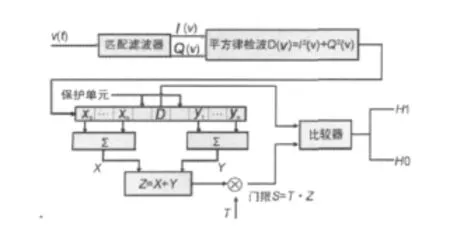
图1 CA－CFAR检测器方框图

在瑞利包络杂波及单脉冲平方律检测的假设下，每个参考单元采样服从指数分布，可得到虚警概率为

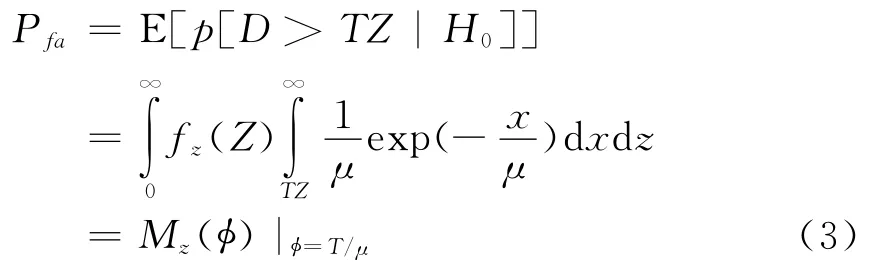
检测概率为

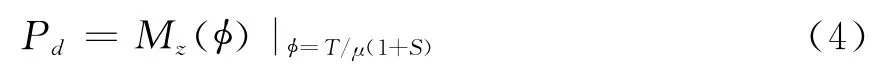
式中：fz（Z）表示 Z 的概率密度函数（PDF）；Mz（·）为随机变量Z的矩母函数（MGF）；矩母函数具有随机变量和的矩母函数等于各随机变量矩母函数之积这一重要性质［4]。

在CA－CFAR检测器中，引入Γ分布，其概率密度函数（PDF）形式为

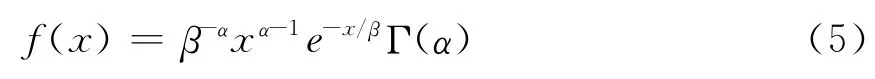
服从Γ分布的随机变量记X～G（α，β），则X的矩母函数Mx（φ）为

根据IID瑞利包络均匀杂波背景假设，可以得到xi～G（1，μ），根据随机变量和的矩母函数等于各随机变量的矩母函数之积这一性质得到Z～G（N，μ），将（6）式代入（4）式可以得到CA－CFAR检测器的检测概率

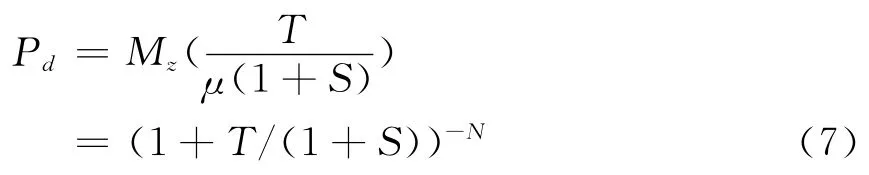
虚警概率可表示为

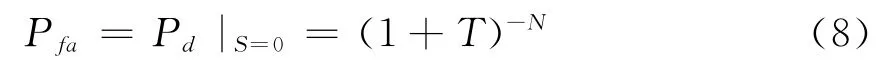
其中，T为标称化因子，在给定虚警概率和滑窗长度的情况下，T可由式（8）计算得到，表1给出了在不同虚警率和滑窗长度情况下的几个常用T值。

表1 不同虚警率和窗长下的T值

在CA－CFAR检测器中，背景杂波功率的估计Z为参考滑窗内N个杂波样本功率的算术平均，在独立同分布（IID）瑞利包络均匀杂波背景条件下，为Z的充分统计量。为方便计算，常将因子1／N归到标称系数T中，得到

图2为CA－CFAR检测实例。仿真杂波数据为背景功率为14dB的IID瑞利包络杂波序列，在第350个距离单元内注入一个非起伏目标。参考滑窗长度N＝32，根据（8）式计算得到标称系数T＝0.333 5，最终得到CA－CFAR检测门限，图2中用虚线表示。

图2 检测实例（N＝32 Pfa＝10－4）

2 CFAR中有限参考单元数对虚警性能的影响

在进行CFAR处理时，参考单元数N是有限的。如果仍采用理论的检测门限值，将使虚警率Pfa大大增加。这是由于杂波平均值的估值偏离了统计均值而产生起伏，在门限系数一定时引起了门限起伏，使杂波超过起伏门限的可能性增加［5]。显然，Pfa的增加与N的大小有关，N越小，平均值估值的起伏越大，Pfa越高；反之，N越大，相对于理论值的增加就越小。表2给出了在虚警率Pfa＝10－4，不同的滑窗长度N的情况下的T值，有表格也可以看出滑窗长度越大，T值越小，从而门限波动越小。