GPS广播星历参数拟合的雅可比矩阵数值导数计算方法①
2012-07-23邢志成王解先
邢志成,王解先
(同济大学 土木工程学院 测量与国土信息工程系,上海200092)
0 引 言
用户利用GPS广播星历参数可以计算出GPS卫星的位置,继而解算用户的位置;反过来,也可以利用GPS卫星的位置,拟合出广播星历的参数[1-2]。GPS广播星历就是由地面控制中心在确定卫星轨道的基础上,以卫星的位置作为观测量拟合出广播星历参数再上传给卫星,然后,卫星再转发这些星历参数给用户[3]。
利用最小二乘原理拟合广播星历参数的过程中,偏导数矩阵的求解有解析法和数值导数法两种方式。前者需要推导位置矢量对待估参数的偏导数,形式复杂,若改变参数形式,偏导数的形式需要重新推导;与前者相比,数值导数计算方法形式简单,计算方便,便于计算机操作[4]。采用数值导数计算方法,利用IGS精密星历卫星坐标数据,根据最小二乘平差原理拟合出GPS广播星历的15个参数;并分析了计算参数的雅可比矩阵时,增量δ的选取对拟合精度和效率的影响,得出了一些结论。
1 GPS广播星历参数拟合算法
GPS广播星历参数以开普勒轨道根数为基础,加上表示轨道摄动调和系数以及随时间的变化率,一共有15个:6个开普勒轨道根数ω,Ω0,M)和9个摄动力参数(Δn,i,Ω,Cuc,Cus,Crc,Crs,Cic,Cis).15个参数的具体意义参考文献[2].
1.1 由广播星历计算卫星位置
若要计算时刻t卫星的空间坐标,根据广播星历参数,按如下步骤计算:
1)求长半轴A
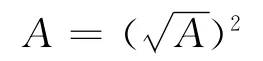
2)计算平角速度n0

3)计算从需要时刻到参考时刻的时间差tk
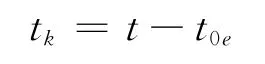
4)改正平角速度n
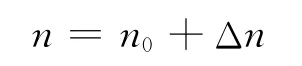
5)计算平近点角Mk
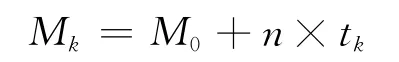
6)按下式迭代计算偏近点角Ek
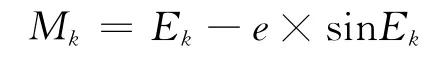
7)由下式计算真近点角

8)计算纬度参数φk

9)周期改正项
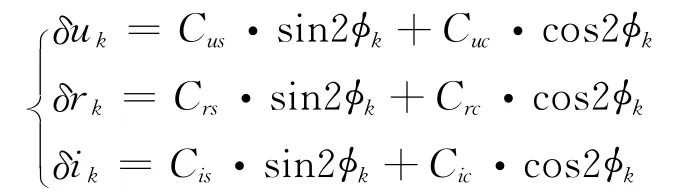
10)计算改正后的纬度参数uk
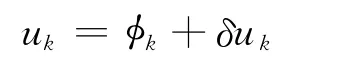
11)计算改正后的向径rk
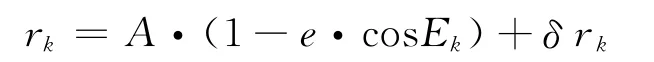
12)计算改正后的倾角ik

13)计算卫星在轨道平面内的坐标(xk,yk)
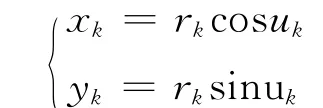
14)改正升交点的经度
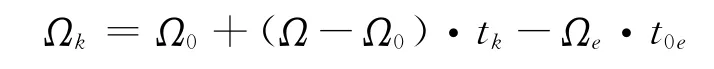
15)最后计算卫星在地固坐标系中的坐标Rk=(XkYkZk)
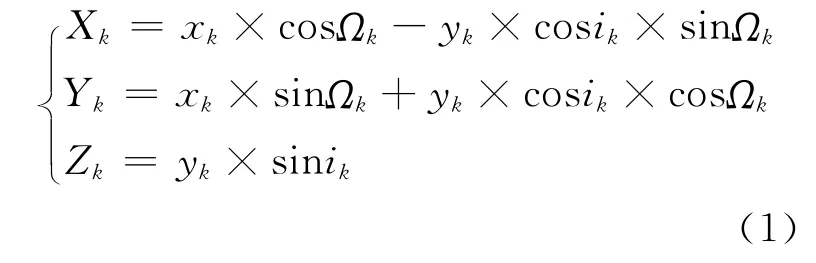
1.2 数值导数的概念及雅可比矩阵的确定
若y=f(x1,x2,…,xi…),y到xi的导数的定义为[5]
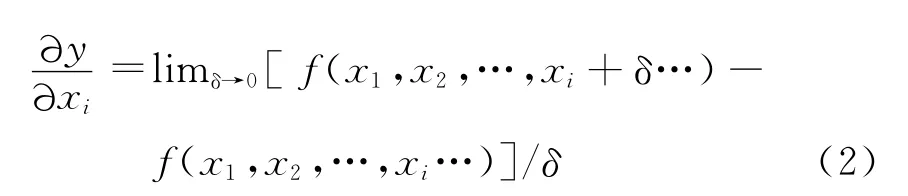
当δ足够小时,这一导数可以近似写成数值导数的形式
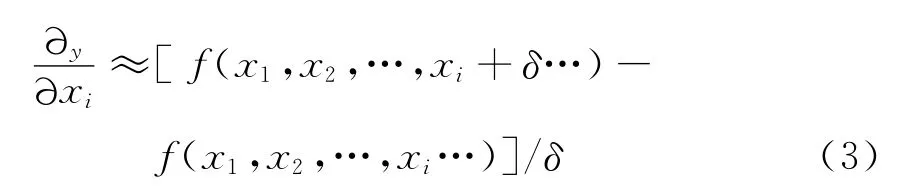
结合1.1节,则一组卫星坐标Rk=(XkYkZk)到Xi(i=1,2,…15)的雅可比矩阵可表示为
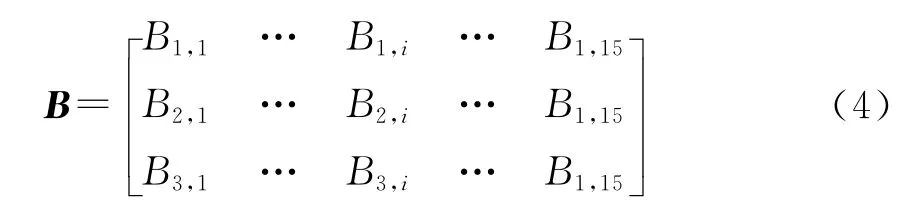
若利用同一颗卫星的上下各5个历元共11组坐标,则可以得到式(4)的参数的雅可比矩阵B.
1.3 平差模型
对于给定的参考时刻t,设参数为Xi(i=1,2,…15),由一个历元的卫星坐标Rk=[XkYkZk]T,就可以根据式(1)建立如下的误差方程

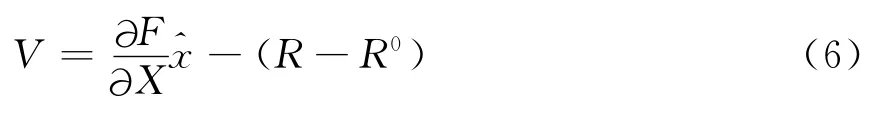
式(6)中的R0代表R的近似值,X0代表X的近似值,F(X0)=R0.
则(6)式可以写为

式(7)中L=(R-R0)(根据最小二乘原理,利用间接平差求解,可得
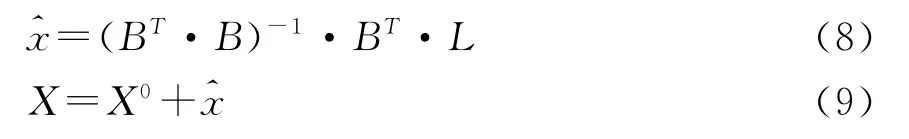
通过式(5),对每个历元的卫星坐标可列出3个误差方程,若选取11个历元,那么一共有33个方程,对于15个参数,进行间接平差迭代求解。迭代的收敛条件为:|σi+1-σi|/σi<ξ,其中,ξ是预先给定的阈值,取1.0e-05.是第i次迭代的单位权方差[2]。
2 算例分析
使用2010年1月1日从0时45分到3时15分第02颗GPS卫星的共11组IGS精密星历数据(间隔15min)。15参数中六个轨道根数的初值如表2所示,其余的9个参数初值设为0.

表2 六个轨道根数初值
为了比较小量δi的取值对拟合精度和效率的影响,算例根据1.2节所述的方法,利用公式Δ=f(x1,x2,…,xi+δ…)-f(x1,x2…,xi…)得到的差值Δ所在的量级不同,采用12种方案确定增量δi的取值,分别为:Δ量级为千万米级、百万米级、十万米级、万米级、千米级;百米级、十米级、米级、分米级、厘米级、毫米级、微米级。当然,增量的取值对计算结果的影响和计算机的性能有很大关系,本算例是在32位操作系统下完成的。根据这个方法可以确定增量δi的取值范围。表3列出了方案8米级的增量δi的取值。
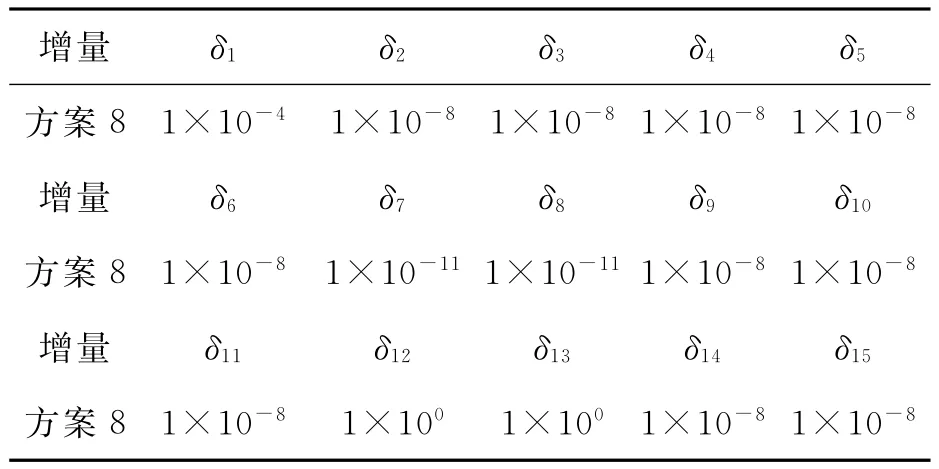
表3 第8种方案“米级”增量δi的值
根据不同的方案,采用1.3节所述的算法进行计算。计算迭代的次数统计如表4所示。
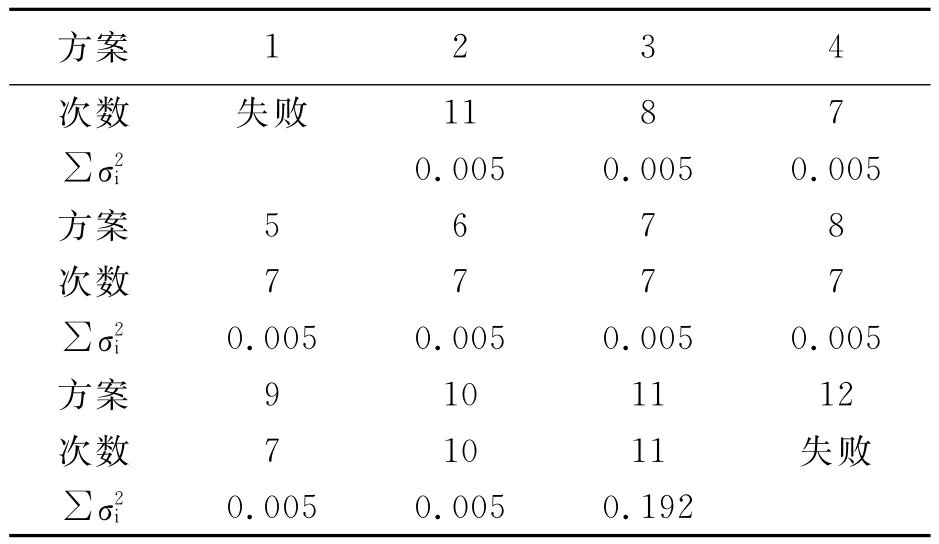
表4 12种方案统计
表5给出了方案8拟合出的广播星历15参数与GPS广播星历15参数的差值。

表5 拟合参数与广播星历参数之差Δ
图1给出了利用方案8拟合出来的广播星历参数计算11颗卫星的坐标与IGS精密星历差值。
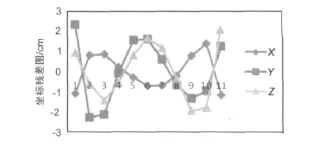
图1 方案8米级小量计算坐标残差
3 结 论
1)通过表4和图1可知,在最小二乘原理的基础上,选取适当的小量,利用数值导数计算方法可以有效地拟合出GPS广播星历,其拟合结果GPS位置与IGS精密星历坐标仅在厘米范围有差别。
2)当小量对卫星位置的影响为万米到厘米时,可以拟合出广播星历15参数,拟合中迭代计算的次数较少,拟合出的参数与GPS广播星历给出的参数值基本一致。当小量超出上述范围时,拟合精度和效率降低,甚至有可能导致拟合失败。
3)采用方案4至9对拟合的效率和精度都没有明显的差异,说明方案4到方案9都是比较理想的预定小量的方法。
[1]郝金明.利用地面测轨资料拟合GPS广播星历[D].郑州:解放军测绘学院,1989.
[2]吕志伟,易维勇,曾志林.GPS广播星历参数拟合算法及其分析[J].测绘科学技术学报,2010,27(2):83-86.
[3]陈刘成,韩春好,陈金平.广播星历参数拟合算法研究[J].北京:测绘科学,2007,32(3):12-14.
[4]王解先,徐志京.三种坐标间转换的雅克比矩阵数值导数计算方法[J].大地测量与地球动力学,2004,24(4):19-23.
