基于模糊PI控制的永磁同步直线电机调速系
2012-07-16张海啸刘亚涛
张海啸 刘亚涛
(1.太原重工股份有限公司技术中心,山西太原 030024;2.太原市热力设计有限公司,山西太原 030002)
0 引言
永磁同步直线电机(PMLSM)兼有永磁电机和直线电机的双重优点,与直线感应电机相比,PMLSM具有指标高、体积小、重量轻等优点,因而不断在许多领域得到了应用。例如垂直升降输送系统、高速地面运输系统、往复式空气压缩机等等,其潜在的理论价值和技术经济效益巨大,应用前景十分宽阔。
PMLSM调速系统本身就是一个有较强非线性、多变性及强耦合的复杂系统,考虑到系统运行过程中受到的干扰因素,控制起来比较困难。因此,寻找一种合适的控制策略具有重要的意义。传统的PID控制过分依赖于控制对象模型,参数鲁棒性较差,抗扰动能力不太强,对于PMLSM这样复杂的调速系统很难满足控制要求。模糊控制系统的鲁棒性强,干扰和参数变化对控制效果的影响被大大减弱,尤其适合于非线性、时变及纯滞后系统的控制。自适应模糊PI控制通过模糊控制规则自动整定控制器参数,大大改善了系统的稳态精度和动态响应,文中首先介绍了PMLSM矢量控制系统的基本原理,然后对基于SVPWM脉宽调制的PMLSM矢量控制调速系统进行阐述,重点研究了自适应模糊PI控制方法,对该控制方法进行了理论分析并建模仿真,仿真结果表明自适应模糊PI控制策略可以大大改善PMLSM矢量控制调速系统的控制性能。
1 PMLSM矢量控制系统
1.1 d轴—q轴坐标系PMLSM数学模型
在建立d轴—q轴下数学模型之前,针对PMLSM的特点,先作以下几点假设:初级上没有阻尼绕组;不计涡流及磁滞损耗;忽略铁心饱和;反电动势波形为正弦分布;永磁也没有阻尼作用。这样做可以忽略一些影响较小的因素,简化分析过程,根据坐标变换理论,可得出d轴—q轴坐标系下PMLSM的数学模型。

其中,id,iq分别为电枢绕组d轴、q轴电流;ud,uq分别为电枢绕组d轴、q轴电压;Ld,Lq分别为电枢绕组d轴、q轴电感;R为电枢绕组电阻;p为电机极对数;M为动子质量;B为粘滞摩擦系数;v为动子运动线速度;τ为初级绕组极距;ψPM为永磁体磁链;Fd为负载推力。
1.2 PMLSM矢量控制系统
矢量控制实现的基本原理是通过测量和控制定子电流矢量,根据磁场定向原理分别对产生磁场的电流分量(励磁电流)和产生转矩的电流分量(转矩电流)进行控制,从而实现对负载扰动和参考值变化的快速响应。PMLSM的矢量控制最终目的是对电机初级电流的控制。由PMLSM数学模型中推力等式知,PMLSM的电磁推力大小基本上取决于初级直轴和交轴电流分量,在矢量控制方式下,采用了按动子磁链定向(id=0)的控制思想,使初级电流矢量位于q轴,无d轴分量,即初级电流全部用来产生转矩,此时,PMLSM的数学模型可写为:
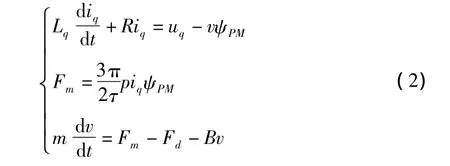
由式(2)知,PMLSM的推力只与电枢交轴电流的幅值成正比,实现了解耦控制。此种控制方式较为简单,由位置传感器测得PMLSM的实际位移S,将直线运动产生的直线位移S转换为类似旋转电机转子的角位置θ,有只要准确地检测角位置θ,便可控制逆变器让三相初级的合成电流即磁动势位于q轴上,此时,PMLSM的电磁转矩只与初级电流的幅值成正比,那么,控制初级电流的幅值就可以很好地控制电磁转矩,此时的控制方式类似直流电机的控制,能够得到满意的推力控制特性。PMLSM的控制系统的原理图如图1所示。主回路由空间电压矢量(SVPWM)逆变器、三相整流电路、PMLSM本体、电流检测回路及位置传感器等组成。控制回路由电流控制器、速度控制器、驱动电路及PWM生成器等组成。
首先根据位置传感器检测到的速度S计算出的动子速度v,将其与设定参考速度vref进行比较,再通过模糊PI调节器的分析,计算出初级交轴电流的参考输入isqref,此时控制直轴电流isdref=0,经坐标变换将电流检测电路检测到 id,iq,转换得到 isd,isq,将isd,isq分别与它们的参考给定isdref,isqref进行比较,通过两个电流PI调节器的分析计算得到合适的控制量。由转速外环和电流内环构成了PMLSM的双闭环控制系统。该控制系统中采用了空间电压矢量脉宽调制(SVPWM)技术,由于SVPWM电压利用率高、开关损耗小、谐波少等优点,大大改善了PMLSM的调速性能。

图1 PMLSM矢量控制原理图
2 模糊PI复合控制器的设计
2.1 控制方案的设计思路
PMLSM矢量控制系统应用电流、速度双闭环控制策略。电流环仍采用传统PI电流控制,速度环采用自适应模糊PI控制方式,模糊控制方法对被控对象的时滞、非线性和时变性具有较强的适应能力,对干扰或噪声具有更强的抑制功能,即更强的鲁棒性,但消除系统稳态误差的性能比较差,难以达到较高的精度。PI控制对参数确定的模型具有快速性好、精确度高的特性,综合两者的优势,提出自适应模糊PI控制方法。自适应模糊PI控制器分两步进行设计,首先在不考虑模糊控制的前提下,用工程方法计算PI参数,然后依据已有的系统控制原理,运用模糊控制策略,对PI参数进行在线的调整计算,适当地增加或减小控制力度,使输出尽快跟随给定速度。基于这种思路来设计自适应模糊PI控制器,实时计算工作量小,物理意义明确,便于工程运用。
2.2 自适应模糊PI控制器的设计
设计中使用的是一个两输入E,EC,两输出Kp,Ki的二维模糊控制器,将电机给定转速和实际转速间的偏差E,以及偏差变化率EC作为模糊控制器的输入变量,计算出PI控制器的两个控制参数与偏差及偏差变化率之间的模糊关系,运行过程中不断检测E和EC,再依据模糊控制原理来对两个参数进行在线修改调整,以满足不同E和EC时对控制参数的不同要求。
原理图如图2所示:▽Kp,▽Ki为模糊控制器的输出,Kp,Ki为工程方法整定的PI参数,根据被控制对象的状态在线自动调整PI参数,由此实现PI参数的在线自适应调整。设计步骤如下:
1)模糊控制器的输入输出语言变量各分为七个模糊子集,分别用语言变量{正大(PB)、正中(PM)、正小(PS)、零(ZO)、负大(NB)、负中(NM)、负小(NS)}表示,并规定其隶属度。输入输出变量的论域均为{-3-2-1 0 1 2 3},输入输出语言变量服从的隶属函数如图3所示。

图2 自适应模糊PI控制器原理图
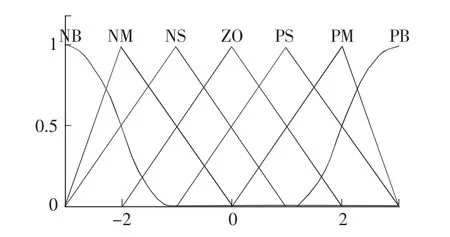
图3 输入输出变量的隶属度函数
2)模糊控制规则表及模糊输出曲面。模糊决策采用Mamdani型推理算法,总结以往工程实际操作经验得到的PI参数调整原则,可以得到输出变量Kp,Ki的控制规则表如表1所示。

表1 输出变量的控制规则表
3 仿真分析
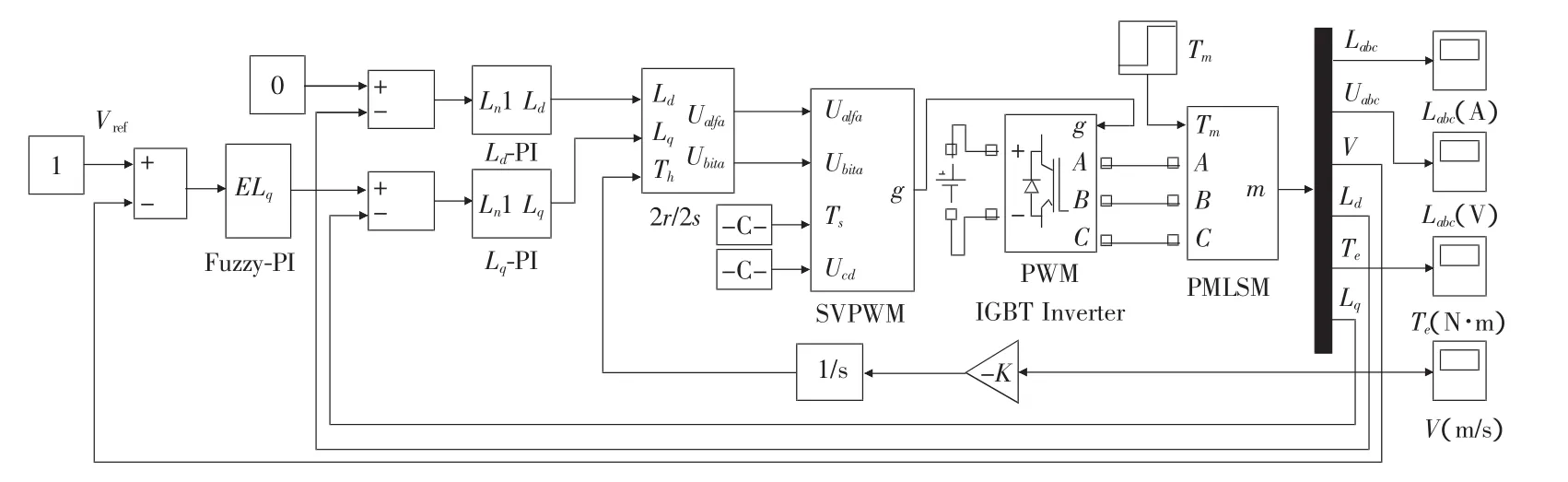
图4 基于模糊PI复合控制的PMLSM矢量控制系统仿真结构图
系统建模仿真主要目的是考察自适应模糊PI控制器在改善控制性能方面的作用,在MATLAB7.0/SIMULINK下进行建模仿真。PMLSM的参数:初级电枢d轴,q轴电感Ld=Lq=18.74 mh;初级电枢电阻R=1.252 Ω;动子质量m=25 kg;极距τ=36 mm;极对数P=2;永磁体磁链Ψf=0.286 Wb;粘滞摩擦系数B=0.2 N·s/m;目标速度给定值vref=1 m/s。基于自适应模糊PI控制的PMLSM矢量控制系统仿真结构如图4所示,为了验证所设计的PMLSM控制系统的性能,文中进行了系统加载启动、突改负载的仿真,得到系统速度仿真曲线如图5所示。
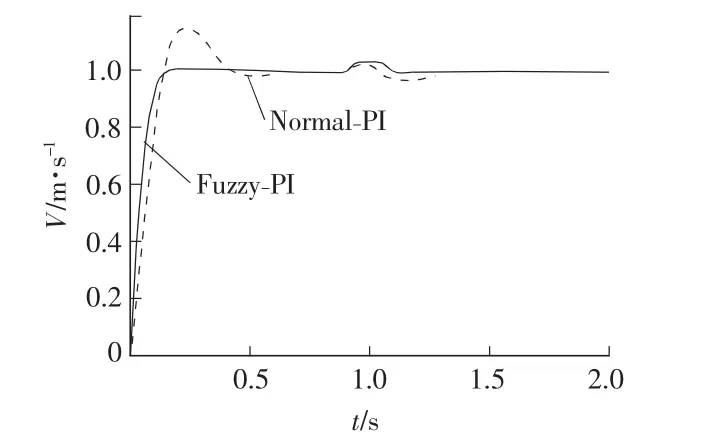
图5 PMLSM控制系统速度仿真图
仿真设置:初始给定速度为1 m/s;负载推力为80 N,0.9 s时负载推力由80 N突减为60 N。速度仿真曲线如图5所示。
经分析发现,采用模糊PI复合控制较传统的PI控制具有更强的鲁棒性,启动快,超调量小,调节时间减少,系统响应速度增加。当负载推力从80 N下降到60 N时,传统PI控制出现了5%的速度波动,并经过0.2 s才能恢复稳定;而模糊PI复合控制受到负载干扰冲击要小,速度波动和恢复稳定的时间分别为2%和0.1 s,后者在上升时间,超调及静差方面均优于常规PI控制。
4 结语
基于自适应模糊PI控制策略的PMLSM矢量控制系统,充分利用MATLAB软件模糊逻辑工具箱的强大功能,根据系统的数学模型,建立仿真模型。模型简单、合理,仿真速度快,结果接近实际情况,对系统的实际运行具有可靠的理论参考价值。仿真结果表明,和PI控制相比该策略具有更好的动态、稳态性能,证明了该控制系统的合理性。
[1]唐任远.现代永磁电机理论与设计[M].北京:机械工业出版社,1997.
[2]李志明,张遇杰.同步电动机调速系统[M].北京:机械工业出版社,1996.
[3]王建宽,崔 巍,江建中.SVPWM技术的理论分析及仿真[J].微特电机,2006(6):15-18.
[4]刘红钊,付子义.永磁直线同步电动机垂直运输系统模糊控制策略的研究[J].机电工程技术,2007,36(2):13-15.
[5]刘红波,李少远,柴天佑.一种基于模糊切换的模糊复合控制器及其应用[J].控制与决策,2003,18(5):615-616.
