弹性压杆稳定问题的ODE解法

徐杏华，李 朝

(1.孝感学院城市建设学院，湖北 孝感 432000，2.长春市轨道交通集团有限公司，吉林长春 130012)

在结构设计中，需要对结构进行强度验算和稳定验算，然而对于以受压为主的结构来说，其结构更容易失稳。压杆作为结构失稳的典型代表，它的失稳，轻则引起构件失效，重则引起整个结构的破坏，造成严重的事故。在压杆稳定问题研究方面，楚中毅等［1，2］对稳定问题的精确解法做了一些探讨，龙驭球［3］也从不同角度总结了稳定问题的各种解法。然而对于无限自由度杆系结构线性稳定问题，解析法求解的精度往往与其计算时所选取的挠曲线的函数形式有很大的关系，利用普通结构力学的方法根本不能得到精确解［4］，而采用常规有限元法，往往需要对网格进行细分，这样做不仅计算量大、计算效率低，而且结果也不够精确。

随着常微分方程(即Ordinary Differential Equation，简记作ODE)数值解法的发展，尤其是近10年来一系列常微分方程求解器(即 Ordinary Differential Equation Solver)通用程序相继问世［5，6，7］，使直接针对结构稳定问题的数值解析法成为可能。对于一般的平面杆系结构，常微分方程求解器不仅可以给出精确的临界荷载和相应的失稳变形形态，而且还可以给出高阶失稳荷载和形态。本文推导出了无限自由度弹性压杆稳定问题的控制微分方程，算例结果与解析解以及常规有限元解的比较表明该方法的求解精度和效率较高。

1 压杆的挠曲线方程

1.1 控制微分方程的推导

考虑图1所示的最具一般性的压杆，其支撑端可以同时受三个力作用，即:压力P，约束反力R和约束力偶矩M0，相应的弯矩方程应为:

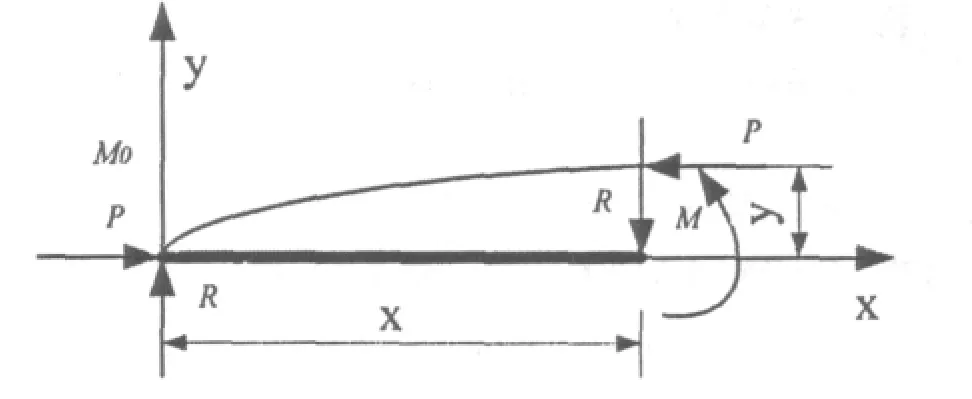
图1 压杆受力状况Fig.1 Stress state of compression bar

1.2 控制方程的标准化

由于常微分方程求解器是按照标准的ODE形式研制的，只具有求解标准的非线性常微分方程问题的功能，不具有直接求解特征值问题的功能［5］。因此对于上述关于边值问题的常微分方程组的特征值问题，应该利用一些ODE变换技巧将其转换为COLSYS［7，8］所能接受的标准的非线性常微分方程形式。为此需做以下工作:

区间映射:利用区间映射技巧进行坐标变换，将非规则的求解区间映射到确定的标准单位区间，即将待定的特征值问题定义在标准区间［0，1］上，使结构的每一个单元结点处的坐标都为0或1(如图2)。例如:对于一长度为L的单元，我们可令

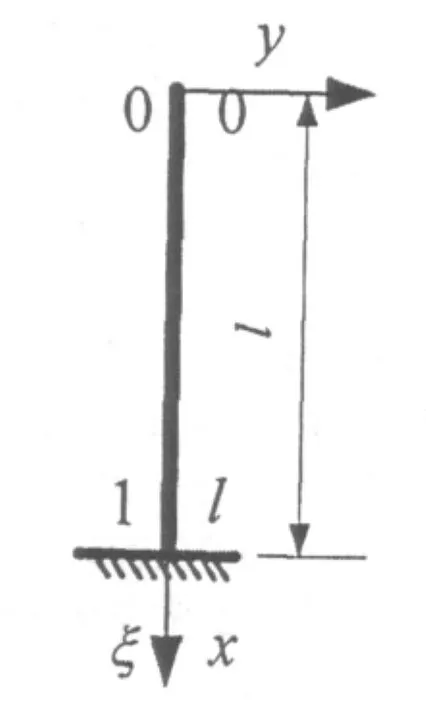
图2 坐标转换图Fig.2 Diagram of coordinate transformation

经坐标变换后，此变截面压杆的挠曲线方程可转化为:

式中λ=P，Y=Y(ξ)，()＇=d()/dξ，n表示因结构刚度或质量变化而将结构划分的段数。

(2)构造平凡ODE:为将特征值转化为标准的非线性ODE问题，需要为待定的特征值建立一个平凡ODE，从而保证λ为常数的前提下，将它引到ODE中求解。即

(3)构造等价ODE:将一重积分问题转换为一阶常微分方程问题，以便于COLSYS求解，即取振型归一化条件为

这一归一化条件相当于将Rayleigh商中的分母取为单位值，对上式(4)进行坐标变换后，有

再利用等价的ODE技巧将以上积分式转换为标准的ODE问题

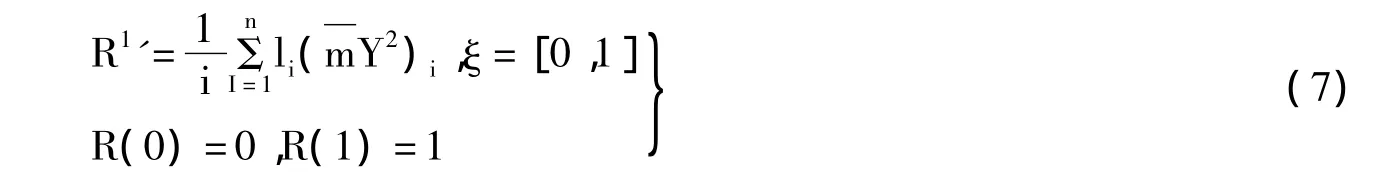
这样既可以计算定积分求解上式，又可以将某些积分条件(如归一化条件)化为等价的ODE提法而加入原问题求解。于是式(3)、式(4)、式(7)便形成了一组标准的非线性的常微分方程组，在进行计算时，只要用户提供一个适当的初始解，就可直接利用标准的常微分方程求解器的非线性功能进行求解。

2 求解器解法程序结构及其调用

常微分方程求解器主要是通过调用常微分方程边值问题通用程序COLSYS来实现其求解功能的，它是目前最为可靠的常微分方程边值问题求解器之一，也是面向常微分方程常用的支撑软件。COLSYS是以子程序的形式由用户进行调用，在调用时只需要用户为COLSYS提供某些参数。例如:每个子区间的配置点数，初始区间网格划分的子区间数，给定误差限的解分量、误差和误差限值以及导数的数目，初始网格的划分，非限性问题初始解的提供形式，非线性问题是否是敏感型等。

控制微分方程及其相应的边界与连接条件的编程求解是工作的核心部分，这个模块需要用户根据具体的问题在外部定义FSUB、DFSUB、GSUB、DGSUB、SOLUTN五个子程序以供调用。下面将详细地介绍这五个子程序的功能:

(1)FSUB是一个提供常微分方程信息的子程序名。值得注意的是在进行编程求解前，应先利用ODE变换技术将这些常微分方程转换为能够为COLSYS所接受标准的非线性常微分方程形式，以便使结构的每一个单元结点处的坐标都为0或1。

(2)DFSUB是一个计算FSUB中常微分方程的雅可比矩阵的子程序名。

(3)GSUB是一个提供边界条件与连接条件的子程序名。

(4)DGSUB是一个计算GSUB中Gi(X，Z)的雅可比矩阵的子程序名。

(5)SOLUTN是一个计算非线性问题初始解的子程序名。只有求解非线性问题时才会用到此子程序。

除以上5个外部子程序外，还需编制一些辅助子程序，以及主程序和子程序之间的联系程序单元即接口块，这样一个完整的调用COLSYS求解器解决ODE问题的程序结构即告完成，可以进行线性或非线性ODE体系问题的编程计算。

3 算例与计算结果分析

计算图3所示为一悬臂压杆的临界荷载和失稳模态。其中弹性模量E=1，截面惯性矩I=1，杆长l=1，初始轴力P=10。该问题的理论解答为Pcr=π2EI/(2l)2=2.46740110，表1为本文方法的计算结果，表2为常规有限元法的计算结果。

图3 悬臂压杆及其失稳模态Fig.3 Cantilever bar and corresponding instability mode

表1 ODE解计算结果Table 1 Result of ODE method

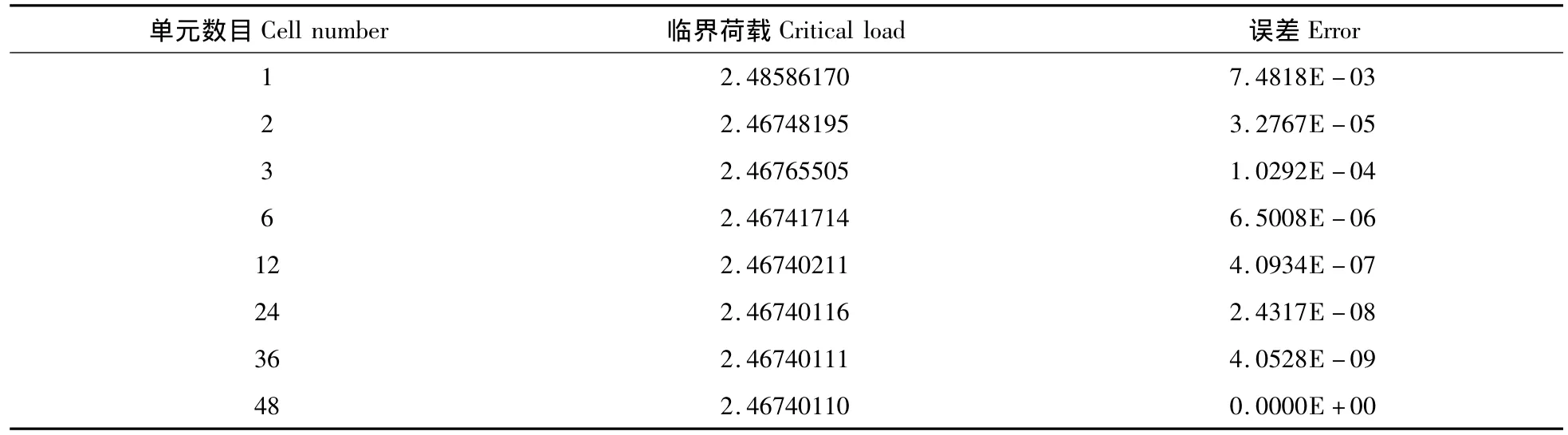
表2 常规有限元法的计算结果Table 2 Result of conventional finite element method

从表1、2可以看出，本文ODE解只用了3次迭代就求得弹性压杆稳定问题的精确解，而利用常规有限元法需要将结构划分为48个单元格，才求得相应精度的解，说明对于相同精度的解答，本文方法的计算效率明显高于常规有限元法。此外，该方法还具有使用方便、计算量少、收敛速度快等优点。

4 结论

本文提出的常微分方程求解器解法，采用数次迭代就可以得到所求问题的精确解，不需要对单元进行细分，而且该方法从计算精度和计算效率上均优于常规有限元法，并且其精度可由用户所任意指定，使用操作也相当方便。由此可预见，这种常微分方程求解器数值解法的应用前景是相当广阔的。

［1］楚中毅，陆念力，楚兰英，等.梁杆结构稳定性分析的一种精确有限元方法及其优化［J］.建筑机械，2001，9(14):68－72

［2］楚中毅，陆念力，车仁炜，等.一种梁杆结构稳定性分析的精确有限元法［J］.哈尔滨建筑大学学报，2002，4(5):25－28

［3］龙驭球，包世华.结构力学［M］.北京:高等教育出版社，1999

［4］任凤鸣，范学明.弹性压杆稳定问题的精确解法［J］.建筑科学，2008，24(3):12－14

［5］包世华.结构力学Ⅱ［M］.北京:高等教育出版社，2001

［6］包世华，周 坚.薄壁杆件结构力学［M］.北京:中国建筑出版社，1991

［7］A scher U，Christiansen J and Russell R D.Collocation Software for Boundary－value ODE［J］.ACM Trans Math Software，1981，7(2):209－222

［8］A scher U，Christiansen J and Russell R D.Algorithm 569，COLSYS:Collocation Sof tware for Boundary－value ODEs［J］.ACM Trans Math Sof tware，1981，7(2):223－229