核机器学习方法及其在生物信息学中的应用
2012-07-16牟少敏曹学成
王 蕊,牟少敏,曹学成,苏 平
(1.山东农业大学机械电子与工程学院,山东 泰安 271018;2.山东农业大学信息科学与工程学院,山东 泰安 271018)
机器学习(Machine Learning)是根据训练样本找出输入/输出数据之间的相互依赖关系估计,对未知的输出样本做出尽可能准确的预测或分类[1]。目前,随着计算机技术的飞速发展,数据的采集速度和存储技术都有了极大的提高,产生了各种大量的数据信息,需要人们对其进行合理的预测或分类,为科学决策提供有力的依据。因此,机器学习的研究具有非常重要的意义。而基于核的机器学习方法(简称:核方法)则以其优越的性能吸引了众多研究人员的关注,成为机器学习领域的研究热点之一。
核方法理论的研究工作可以追溯到1909年,Mercer首先在泛函分析中提出了再生核(Mercer核)和再生核Hilbert空间[2]。1950年,Aronszajn等人对其进行了进一步研究和完善[3]。1964年,Aizerman等人将再生核技术用于学习理论的证明[4]。1995年,统计学习理论的创始人Vapnik利用“核技巧”(Kernel trick),即通过在特征空间中引入核函数代替内积,构建了一种基于统计学习理论的核方法—支持向量机(Support Vector Machine,SVM)[1,5]。该方法广泛地应用于图像处理、文本分类和网络安全等领域[49],推动了核理论和核机器学习研究工作进一步地深入开展。
近年来,国内外研究人员相继提出了许多不同的核方法以及针对支持向量机的改进算法,使得核理论不断地完善,核方法的应用领域不断拓展。1998年,Sch·lkopf等人对线性主成分分析(Linear Principal Component Analysis,LPCA)方法进行核化,得到了相应的核主成分分析(Kernel Principal Component Analysis,KPCA)方法[6]。核典型相关分析(Kernel Canonical Correlation Analysis,KCCA)则是由 Mika等人于1999年提出的[7],是模式识别中进行特征提取的重要技术。核聚类(Kernel Clustering,KC)[8]是基于核的聚类方法。其利用非线性映射,把输入空间的样本通过一个非线性变换映射到一个高维特征空间中,对变换后的样本再进行聚类分析。
而对支持向量机的研究工作主要集中在以下几个方面,降低支持向量机的计算复杂度、直推式学习、多类问题的分类、增量学习和核函数的研究,不少的研究人员提出了许多改进的算法。
1998年,Vapnik提出了一种半监督机器学习的方法,即直推式支持向量机[9]。它是将无标号和有标号数据作为训练集,而训练集中仅含有少量有标号和多数无标号的样本点,大大减少了对有标号样本的需求。
支持向量机最初是针对二类分类问题提出的,不能直接应用到多类分类问题中[10,11]。因此,如何将二类分类方法有效地推广到多类问题,特别是大类别的分类问题,也是支持向量机理论研究的重要内容之一。
当训练样本数据过大,无法一次性读入内存或在线学习情况下,训练开始时无法得到所需要的全部数据时,可以采用支持向量机的增量学习算法(Incremental Learning)。将训练集分成几个独立的子集,依次在各个子集上作增量学习,这样不仅可以舍去无用的样本,节省内存空间,缩短训练时间,而且可以充分地利用以前的学习结果,使得学习结果具有延续性[12]。
支持向量机的应用受到限制的一个很重要的原因就是需要求解凸二次优化问题,对于大规模样本的数据集,其计算具有较高的时间和空间复杂度。因此,如何在不影响分类性能的前提下,降低计算复杂度,提高学习速度,建立高效的求解支持向量机中的最优化问题算法,成了支持向量机一个很重要的研究方向。常用的算法有选块算法(Chunking Method)[13],分解算法(Decomposition Method)[14-15],序列最小最优化算法(Sequential Minimal Optimization,SMO)[16]。
本文结构安排如下:第1节介绍了核方法及其分类,阐述了核函数的性质和构造高效核函数的方法。第2节是以生物信息技术为背景,对序列数据核函数在生物信息学中的应用进展作了详细介绍。第3节对全文进行总结。
1 核方法
核方法的基本原理是采用非线性变换把输入空间的样本映射到高维的特征空间,从而达到线性可分的目的,对实际应用具有重要的意义。其简单的核函数对应着“复杂”的映射。
通过核方法的基本原理可以看出,设计新的核方法主要有两个关键问题:一是与核函数有关的问题。二是采用何种学习算法和改进学习算法的问题。采用不同的学习算法可以构成不同的核方法,如前面提到的将核函数引入聚类方法可以构成核聚类方法。
1.1 常用核方法的分类
机器学习可分为有监督和无监督的学习。有监督学习所处理训练样本的类别是事先已经标号的,而无监督学习所处理训练样本的类别则是未事先标号的。由于核方法的实质就是将核函数引入到一些模式分类或回归方法中,因此可以将核分类方法也相应地分为有监督分类学习和无监督分类学习两大类。支持向量机主要用于有监督的学习。而常用的无监督核方法有核主成分分析(Kernel Principal Component Analysis,KPCA)[17]、核聚类(Kernel Clustering,KC)、核独立成分分析(Kernel Independent Component Analysis,KICA)[18]等。
另外,与前两种学习方式不同的直推式学习是利用少量有标号的数据和大量无标号的数据进行训练,通常称为半监督学习方法。其相应的核方法可以作为第三类核方法。
1.2 核函数
核函数的思想在现实世界中有着广泛的应用。实际上,如果一个分类或回归问题,涉及到点积运算,那么就可以通过引入核函数将问题映射到高维空间中去解决。核函数(Kernel Function)定义为特征空间的一个点积K(x,y)=φ(x)·φ(y)。由于特征空间的维数一般很高,因此φ(x)的计算较为复杂。支持向量机的一个主要的技巧在于它与一般的降维技术不同,它是利用核函数将特征空间的非线性可分的数据映射高维的希尔伯特空间,达到线性可分的目的,而且不必明确知道映射函数φ,只须在输入空间计算核函数K(x,y)即可,从而大大简化了计算量。目前,核函数的研究工作主要集中在两个方面:一是研究已有核函数的参数如何选取,即核参数选取的优化问题。核参数的选择或优化是能否取得理想的预测结果的重要因素之一,其研究又以高斯核函数为主的较多;二是根据实际应用问题提供的数据,构造新的高效核函数。关于核参数的选择与核函数的构造等问题的研究虽然已经取得了一些进展,但是仍不能令人满意[19-21]。核函数的构造与应用的背景知识有着密切的关系,因为核函数反映的是样本之间的相似性量测,所以在许多研究当中,研究者经常是根据研究领域中找寻其物理、化学、生物意义的相似性,构造一个特殊的核函数。如:结合文本分类[22]和入侵检测技术[23],可以设计出高效的核函数,提高支持向量机的分类性能,如何构造与实际问题有关的核函数,一直是SVM研究的重要课题。本文主要介绍的是核函数在生物信息领域中的应用。
目前,常用的核函数主要有4种,详见表1。实际应用中采用和研究最多的是高斯核函数。

表1 常用核函数Table 1 Usually kernal function
核矩阵(Gram矩阵)则是表示在高维特征空间中,任意一对样本的点积,与核函数有着密切的关系。
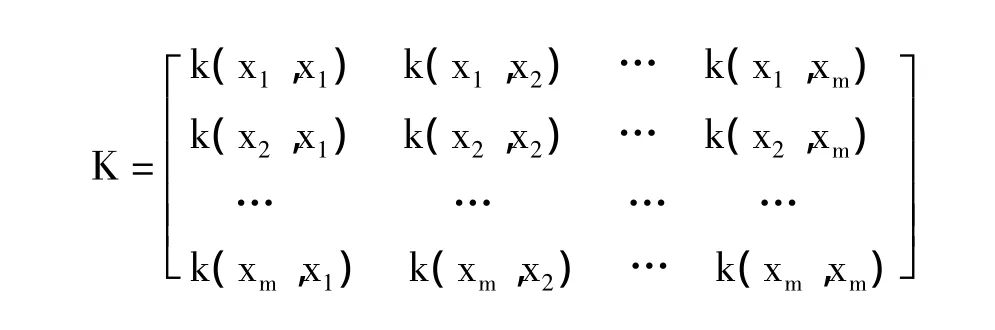
如果核函数是有效的,核矩阵则是对称和半正定的[24]。
支持向量机和其它的核方法的研究工作过去主要是基于属性值的,输入数据一般是定义在向量空间。常用的核函数如:多项式核函数、RBF核函数等对数值问题的分类取得了较好的效果。但是,核函数并不局限于向量空间,很多模式分类问题涉及结构数据,如图、树和序列等,输入数据往往不是长度相等的向量,各分量往往具有不同的语义,不能同等看待。对于序列数据而言,由于缺乏考虑序列数据信息的相似性,效果不佳。现在有的学者开始研究基于结构数据的核方法,即结构模式识别[24],取得了较好的结果。如使用邻域核识别纹理图象[25],使用字符串核和词序列核进行文本分类[26],使用边界化核进行蛋白质分类等[27]。什么是结构数据,现在尚没有统一的定义。一般情况下,文本、图像、空间数据和蛋白质和基因等都可视为结构数据。常用的结构数据的类型有:串、树、图和集合等。如何有效地利用数据的内在的结构信息,构造相应的核函数,对于提高SVM性能,是一项非常有意义的研究工作。
表1的核函数是基于向量空间模型,缺乏利用数据间的结构信息,而且要求向量的长度是固定的。为了克服这一问题,研究人员通常对所专注的领域寻找具有物理、化学和生物意义的相似性,构造一种特殊的核函数即结构化数据核函数。结构化数据核函数常用的类型有字符串核函数、树核函数和图核函数。
目前,字符串核函数在生物信息学领域的应用相当活跃。因此,针对具体的应用,根据数据结构定义相应的核函数,能取得更好的识别效果,提高支持向量机的分类性能,扩展其应用领域。
对于结构化数据,要根据数据的结构信息定义反映数据间相似性的合法的核函数,然后再应用某种核方法对这些数据进行处理。定义结构化数据核函数的方法可按如下方式分类[28]:
(1)利用核函数的运算性质。首先定义每个成分的核函数,然后将这些核函数利用某种运算组合成一个合法的核函数,称为组合核。
主要的代表有卷积核与邻域核。Barzilay等人在纹理识别中采用了邻域核(Neighborhood kernel)以利用数据中的结构知识[29]。卷积核(Convolution kernel)由Haussler提出[30],并应用于字符串核。
(2)直接定义特征空间的一个点积,不需考虑Mercer条件。由于特征空间的维数通常很大,因此需要给出计算核函数的高效算法,称为句法驱动核。
句法驱动核的主要思想是把对象分解成子结构(如子序列、子树或子图),特征向量则由子结构的计数组成。
Leslie等人在蛋白质分类中提出了系列核(Spectrum kernel)的概念[31],在长度为l的字符集上,定义长度为k的字符序列的k-系列核。Collins等人在自然语言处理问题中采用了树核(Tree kernel)[32]。自然语言体现为字符串(句子),但其中隐含着某种句法结构。
(3)利用描述数据的某种模型(如马尔可夫模型)将数据转换成向量空间形式,称为模型驱动核。
(4)利用指数函数将对称矩阵转化成合法的核函数,称为指数核。
指数核(Exponential kernel)由Kondor等人提出[33],其主要思想是矩阵的指数运算可以产生符合正定准则的核。
支持向量机等核方法通常采用的是单核学习,即在学习过程中使用一个核函数。在现实世界中,往往存在大量的数据是针对多数据源或异构数据集的,采用单个核函数的效果不是太理想。例如,输入空间是两个向量组成的空间,第一个向量服从高斯分布,而第二个向量却服从多项式分布。这时,如果仅仅采用一种核函数就显得不足,若用高斯核函数则无法利用第二个向量进行有效划分,而如果采用多项式核函数则由于第一个向量的存在会给分类造成影响。Sonnenburg等人提出了基于多核学习(Multiple Kernel)的支持向量机以及实现算法[34,35]。与单核学习相比,多核学习可以提高分类精度,鲁棒性更强。多核学习用于生物序列数据的分类,也取得了良好的效果[36,37]。目前,如何进一步研究高效的多核学习的方法成为研究核方法的热点之一。
多核学习有两层含义:一是可以一次针对不同的属性选择参数不同的核函数,如根据不同的属性可以选择高斯核函数的不同宽度;二是针对不同的属性选择不同种类的核函数,如根据不同的属性可以在学习过程中同时选择高斯核函数和多项式核函数。使用多个核函数的组合,即使不知道最优参数,也可以通过调整权值找到最合适的参数,显然使用多个核函数的组合要比单个核函数的鲁棒性更强。
1.3 模型选择
支持向量机分类和回归的性能离不开选择一组好的参数,即模型的选择。模型选择包括核函数类型的选择、惩罚因子C的选择、损失函数的选择以及与核函数有关的参数(如RBF核函数的宽度参数,多项式核函数的阶)选择。
目前,参数问题策略主要有两种:一是通过测试非训练样本在某个固定参数上的错误率,然后寻找最优的参数。二是确定学习方法错误率的上界,根据错误率的上界尽可能小来进行参数的选择。最常用的参数优化方法有交叉验证技术(Cross-Validation Technique)。k折交叉验证就是首先将训练集随机地分成k个互不相交的子集,每个折的大小大致相等,利用k-1个训练子集,对给定的一组参数建立模型,利用剩下的最后一个子集的均方差评估参数的性能。重复以上过程k次,然后根据k次迭代后得到的均方差的平均值来估计期望泛化误差,最后选择一组最优的参数。
当k等于训练样本数时,每次迭代只有一个样本作为测试,因此称为留一法(Leave-One-Out)。也有许多研究者提出了许多其它的选择方法,如核校准方法(Kernel Alignment)[38]。
2 生物信息学中的核方法
生物信息学(Bioinformatics)[39]是一个融合了多个学科的领域,包含了分子生物学(如:生物化学、遗传学、结构生物学等)、计算机科学(计算机理论、人工智能、机器学习等)、物理化学和数学(算法建模概率论统计学等)。目前,生物信息学已经成为生物医学、农学、遗传学、细胞生物学等学科发展的强大推动力量,也是药物设计、环境监测的重要组成部分。其不仅具有重大的理论价值,而且具有巨大的应用价值[40]。
生物信息学中,常用的数据类型是各种长度的字符串。生物序列通常被表示成由有限的字符组成的字符串。例如:利用它们可以把蛋白质表示成氨基酸序列,把基因组DNA表示成核苷酸序列,近年来,许多研究人员已经对这种类型的数据进行了了大量的研究。
作为最典型的核方法支持向量机在生物信息学中的应用是相当广泛的,目前主要应用于以下几个方面:蛋白质分类[41,42]、蛋白质结构的预测[43]和微阵列基因表达数据分析[44]。
在生物信息学中,可结合背景知识设计出高效率的核函数。字符串核(String Kernel)是针对变长序列数据定义核函数。结合生物信息的背景知识,如果两个序列同时分享共同的子序列,则这两个序列的相关或相似性高的基本思想,Leslie等人[45,46]定义了一种字符串核(Spectrum Kernel),可以用于蛋白质的分类,其限制条件是不允许字符串之间有间隔,即其相似性量测长度定义为必须完全相同的共同子区域。费氏核(Fisher kernels)是由Jaakkola等人[47]提出的,其将隐马可夫模型(Hidden Markov Models)与支持向量机相结合,基于领域内的背景知识所设计的核函数,它允许在部分信息缺损的情况下,可以进行检测。此法用于蛋白质之间同源相关性的比较,取得了较好的结果。配对比较核 (Pairwise Comparison Kernels)[48]是假设分子的演化主要是通过突变和少量的插入及删除而来,其通过序列的比对,来衡量两个类中对象的相似性,求得一个相似分数,用来构造的核称为配对比较核。
3 结论
本文对核方法的基本原理、常用的核方法和核函数进行了详细的介绍,同时指出了目前核方法的一些研究热点。核方法的研究虽然取得了很多成果,广泛地应用到许多领域。但是仍然存在许多问题需要进一步的深入研究。随着核理论的不断完善和核方法的不断改进,其应用领域也将不断拓展。
[1]Vapnik V.The Nature of Statistical Learning Theory[M].New York:Springer Veriag,1995
[2]Mecer J.Functions of positive and negative type and their connection with the theory of integral equations[J].Philos.Trans.,Roy.Soc.,London,1909,20(9):415-446
[3]Aronszajn N.Theory of reproducing kernels[J].Trans Amer.Math.Soc,2001,12(4):765-775
[4]Aizerman.Theoretical foundations of the potential function method in pattern recognition learning[J].Automation and remote control,1964,25:821-837
[5]Vapnik V N.An overview of statistical learning theory[J].IEEE Transactions on Neural Networks,1999,10(5):988-999
[6]Sch.lkopf B.Nonlinear component analysis as a kernel eigenvalue problem[J].Neural Computation,1998,10(5):1229-1319
[7]Mika S,Ratsch G,Weston J,et al.Fisher discriminant analysis with kernels[M].Hu,Y.H.et al.editors.Neural Networks for Signal Processing,1999,41-48
[8]Girolami M.Mercer kernel based clustering in feature space[J].IEEE Transactions on Neural Networks,2002,13(3):780-794
[9]Vapnik V N.Statistical Learning Theory[M].New York:Join Wiley and Sons,1998
[10]Weston J.Watkins C.Multi-class Support Vector Machines[R].Technical Report,CSD-TR-98-04,May 1998,Department of Computer Science,Royal Holloway University of London,England
[11]Platt J C,Cristianini N,Shawe-Taylor J.Large margin DAGs for multiclass classification[C].In:Neural Information Processing Systems,1999
[12]Syed N A,Liu H,Sung K K.Incremental Learning with Support Vector Machines[C].International Joint Conference on Artificial Intelligence,1999
[13]Cortes C,Vapnik V.Support-vector Networks[J].Machine Learning,1995,20(3):273-297
[14]Osuna E,Girosi G.Reducing run-time complexity in SVMs[A].In:Proceedings of the 14th International Conf.On Pattern Recognition,Brisbane,Australia,1998
[15]Osuna E,Freund R,Girosi G.Improving training algorithm for support vector machines[J].Proc.IEEE NNSP'97.Amelia Island,1997:24-26
[16]Platt J C.Sequential minimal optimization:A fast algorithm for training support vector machines[R].Technical Report MSR-TR-98-14,Microsoft Research,1998
[17]Rosipal R,Trejo L J,Cichocki A.Kernel principal component regression with em approach to nonlinear principal components extraction[R].Technical report,2000
[18]Bach F R,Jordan M I.Kernel Independent Component Analysis[J].Journal of Machine Learning Research,2002,3:1-48
[19]Carl G,Peter S.Model selection for support vector machine classification[J].Neurocomputing,2003,55(1-2):221-249
[20]Chapelle O,Vapnik V,Bousquet O,et al.Choosing Multiple Parameters for support vector machines[J].Machine Learning,2002,46(1-3):131-159
[21]Cristianini N,Shawe-Taylor J,Campbell C.Dynamically adapting kernels in support vector machines[M].Advances in Neural Information Processing Systems,MIT Press,1998,11
[22]Joachims T.Text categorization with support vector machines[C].In:Proceedings of European Conference on Machine Learning,1998
[23]Mu S M,Tian S F.Yin C H.Using Length-weighted Once Kernel to Detect Anomalous Process[C].International Conference on Natural Computation,2007,692-696
[24]G rtner T,Lloyd J W,Flach P A.Kernels and Distances for Structured Data[J].Machine Learning,2004,57:205-232
[25]Barzilay O,Brailovsky V L.On domain knowledge and feature selection using a support vector machine[J].Pattern Recognition Letters,1999,20:475-484
[26]Lodhi H,Saunders C,Shawe-Taylor J,et al.Text Classification using String Kernels[J].Journal of Machine Learning Research,2001,2:419-444
[27]Tsuda K,Kin T,Asai K.Marginalized kernels for biological sequences[J].Bioinformatics,2002,18:268-275
[28]G rtner T.A survey of kernels for structured data[J].SIGKDD Explorations,2003
[29]Barzilay O,Brailovsky V L.On domain knowledge and feature selection using a support vector machine[J].Pattern Recognition Letters,1999,20:475-484
[30]Haussler D.Convolution kernels on discrete structures[R].Technical Report,Department of Computer Science,University of California at Santa Cruz,1999
[31]Leslic C,Eskin E,Noble W S.The spectrum kernel:a string kernel for SVM protein classification[C].In:Proceedings of the Pacific Symposium on Biocomputing,2002,564-575
[32]Collins M.Duffy N.Convolution kernels for natural language[C].In:Neural Information rocessing stems,NIPS 14,2001,http://citeseer.nj.nec.com/542061.html
[33]Kondor R I,Lafferty J.Diffusion kernels on graphs and other discrete structures[C].In:Sammut,C.& Hoffmann,A.editors.Proceedings of the 19th International Conference on Machine Learning,Morgan Kaufmann,2002,315-322
[34]Sonnenburg S,Ratsch G,Schafer C.A general and efficient multiple kernel learning algorithm[C].In:Advances in Neural Information Processing Systems,2006
[35]Sonnenburg S,R tsch G,Sch fer C,et al.Large Scale Multiple Kernel Learning[J].Journal of Machine Learning Research,2006,7:1531-1565
[36]Ratsch G,Sonnenburg S.Learning Interpretable SVMs forBiologicalSequenceClassification[J].BCM Bioinformatics,2004,7(1):S9
[37]Theodoros Damoulas and Mark A.Probabilistic multi-class multi-kernel learning on protein fold recognition and remote homology detection[J].Bioinformatics,2008,24:1264-1270
[38]Cristianini N,Shawe Taylor J,Kandola J,et al.On kernel target alignment[C].In:Proc.Neural Information Processing Systems.Cambridge,A:MIT Press,2002:367-373
[39]周海廷.信息与控制[J].机器学习与生物信息学,2003,32(4):352-357
[40]张春霆.生物信息学的现状与进展[J].世界科技研究与发展,2000,22(6):20-23
[41]刘 青,杨小涛.基于支持向量机的微阵列基因表达数据分析方法[J].小型微型计算机系统,2005,26(3):363-366
[42]C Leslie,E.Eskin and W S Noble.The spectrum kernel:a string kernel for svm protein classi_cation.Russ B.Altman,A.Keith Dunker,Lawrence Hunter,Kevin Lauerdale,Teri E.Klein,Proceedings of the Paci_c Symposium on Biocomputing,2002,564-575
[43]S Hua and Z Sun.A novel method of protein secondary structure prediction with high segment overlap measure:Support vector machine approach[J].Journal of Molecular Biology,2001,308(2):397-407
[44]LIUQing,YANG Xiao-tao.Microarray Gene Expression Data Anlysis Based on Support Vector machine[J],Mini-Micro Systems,2005,26(3):363-366
[45]Leslie C,E Eskin,J Weston,et al.Mismatch string kernels for SVM protein classification,Advances in Neural Information Processing Systems[C].MIT Press,2003
[46]Leslie,C.,E Eskin.The spectrum kernel:A string kernel for SVM protein classiffiation.In:Proceedings of the Paciffic Symposium on Biocomputing.Noble,2002
[47]Jaakkola T,M Diekhans,D Haussler.A discrimitive framework for detecting remote protein homologies[J].Journal of Computational Biology,2000,7(1):95-114
[48]Liao L,W S Noble.Combining pairwise sequence similarity and support vector machines for remote protein homology detection[C].In:Proceedings of the Sixth Annual International Conference on Computational Molecular Biology,2002,225-232
[49]Guanghui Song,Xiaogang Jin,Genlang Chen.Multiple Kernel Learning Method for Network Anomaly Detection International Conference of Intelligent systems and knowledge Engineering,2010,296-299
