基于SAS的调整人群归因危险度评估法在口岸流行病学调查中的应用研究

裘炯良 郑剑宁 施惠祥

(1.宁波出入境检验检疫局 浙江宁波 315012;2.北仑出入境检验检疫局)

1 前言

口岸流行病学调查往往涉及口岸人群中风险因素与传染性疾病的相关性研究，如口岸居民区中房前屋后的瓦罐比率与蚊媒的相关性，以及其导致输入性登革热局部暴发流行的风险性高低评估等。对于单个风险因素与传染病相关性研究可以应用人群归因危险度(Population Attributable Risk，PAR)法来进行综合评估［1-3］。然而，要同时分析多个风险因素与传染病的关联性，这个指标则无法发挥作用。为此，本研究引入调整人群归因危险度法(PARc)，希望对出入境检验检疫机构科学估算由于同时暴露于多种风险因素所引起的传染病发生频率，以及预测防制工作中消除这些因素后该病可被减少或消除的有效程度具有一定的指导意义。

2 原理与方法

2.1 人群归因危险度

指人群中因暴露于某因素所致疾病或死亡所占人群总发病或死亡的百分比。它把病原因子的相对危险度和人群中暴露者的比例结合起来，对某一暴露因素造成的危害程度进行综合评价，是流行病学调查分析中一项很有价值的指标。1953年由Levin ML首次提出，故亦称Levin氏归因危险度(Levin’s Attributable Risk)。

Levin氏法测定PAR的公式：

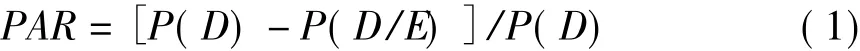
其中，D表示疾病(disease)，E表示暴露(exposure)，P表示概率(probability)。

未调整时的PAR估计：

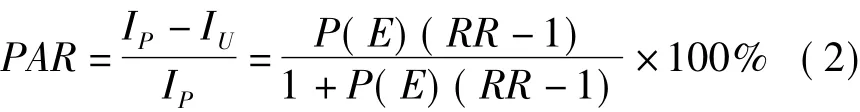
式中：Ip：人群某病发生率

Iu：非暴露者某病发生率

RR：相对危险度(在病例对照研究中可以OR估计)

P(E)：总人群中暴露者的比例

Walter已证明ln(1-PAR)呈正态分布，因此可应用正态分布理论来计算PAR的可信限和进行显著性检验。

2.2 调整人群归因危险度

人群归因危险度仅适用于单变量分析，如资料中有混杂因素或是多个因素同时存在时，上述公式就不再适用，而须计算调整控制一个或多个变量后的PAR指标。这种仅考虑某一危险因素而把其余危险因素均作为干扰因素进行校正后所得的PAR称为调整人群归因危险度，记为PARc。假设研究总体病例数为x，对照数为n-x;K个危险因素(A为研究因素，C为其余校正因子)的不同暴露水平交叉分组构成 J层危险状态(j=0，1，2，….j-1)。一个个体处于第j层是病例的概率为Ij=xj/nj。

式中IC表示当C因素维持原有水平而A因素降为基准水平时，该人群的预期发病率。

PARc计算：若令j*表示第j层A因素降为基准水平，而C因素保持原有水平时的暴露状态。令，式中表示第j层暴露状态相对于第j*层暴露状态的相对危险度，亦即校正C因子的效应后第j层A因素暴露状态的相对危险度;表示第j层暴露状态C因素的相对危险度。由此，A因素的调整人群归因危险度可改写为：

若已知各层在C因素暴露条件下A因素的相对危险度和总体中病例在暴露状态各层分布的比例，即可算得PARc%值。上式中ρj即为第j层暴露状态下病例数占总病例数的比例。

以上为针对研究总体的PARc计算推导。对于流行病学研究的样本人群，其病例是总体病例的一个随机抽样，那么，观察样本中病例在各层的分布比例ρj＇可作为总体病例在各层的分布比例ρj的估计值;而对于发病率很低的传染性疾病，观察资料的校正相对危险度可用多因素Logistic回归模型得出因素的OR值来估计。

3 实例演算

3.1 资料来源

本文应用的数据来自宁波口岸某病流行病学调查资料。采用三阶段整群随机抽样方法，选择对照是以与病例同年龄(10岁为1组)、同性别、同居住地作为1：1频数匹配条件，从自然人群中选择。抽取的143名健康人，其中133例接受流行病学调查，应答率为93.0%;调查方式均为面访;研究的目的是确定某流行病与相关因素的病因学联系。

3.2 资料均衡性分析

对频数匹配的因素(年龄、性别与居住地)进行了均衡性检验，结果表明：病例组平均年龄为26岁(四分位间矩：22-33)，略高于对照组的24岁(四分位间矩：23-31)，将年龄变量转换为以10岁为1组的等级变量后，经χ2检验，P＞0.05;对性别及居住地因素的检验结果显示，病例与对照组之间的分布均匀，差异未达统计学显著性(P值分别为0.230和 0.262)。

3.3 调整人群归因危险度计算

表1为应用多元Logistic回归模型法计算获得该流行病4种风险因素及风险度估计值。

表1 宁波口岸某病风险因素及风险度

表2为该病风险因素的调整人群归因危险度值，分别为：风险因素A所致的流行病危害占11.8%，风险因素B占30.8%，风险因素C占15.9%，风险因素D占38.15%。

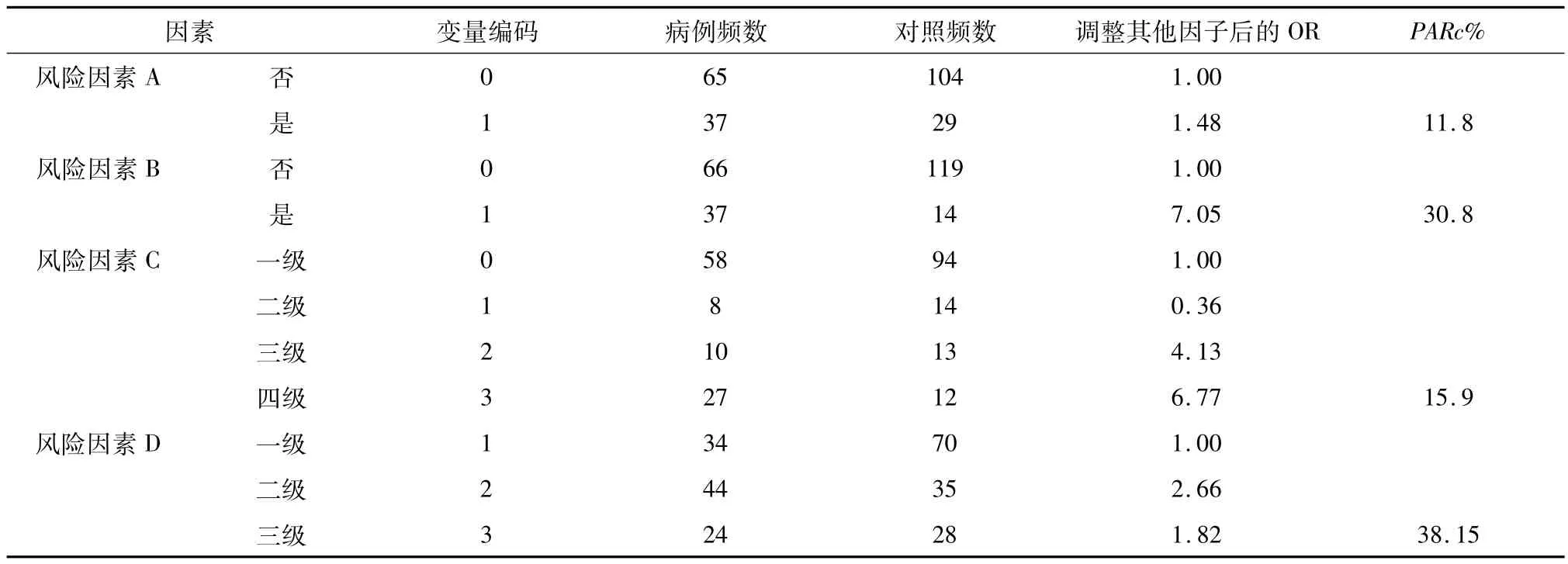
表2 宁波口岸某流行病风险因素的PARc(%)

4 SAS程序实现

笔者自行编制相应的SAS程序代码，如表3所示。在SAS9.2统计软件的“PROGRAM EDITOR”窗口中输入表3的程序代码，单击“RUN”按钮，在“OUTPUT”窗口即可直接查看“数学模型统计学检验”、“数学模型统计学检验结果提示”、“宁波口岸某病风险因素及风险度”及“调整人群归因危险度(PARc%)”等4项结果。表3第04行所列的是口岸流行病学调查中获得的几组风险因素原始数据(为节省篇幅，仅列出部分)，在实际工作中可以根据现场调查结果进行数据替换。

SAS程序首先应用多元Logistic回归模型筛选有统计学意义的风险因素共4种，以似然比检验方法计算整个回归模型的显著性水平，P值=0.0108;SAS进行程序自动判定，给出提示“数学模型检验显示有统计学意义!”;然后，SAS程序自动运算，给出该4种风险因素在校正其他因素前提下的权重系数估计值、标准误、Wald卡方值、显著性检验P值(表1)以及OR值和其95%CI;最后，SAS程序自动对每个风险因素进行卡方分析，给出每个风险因素不同水平的病例和对照数量，同时计算相应的OR值和95%CI，并以公式5运算得出每个风险因素的调整人群归因危险度(表2)。为节省篇幅，表3仅给出计算其中一个风险因素的PARc%所需的SAS程序源代码，其他风险因素的PARc%计算程序同理可得。

表3 实现调整人群归因危险度计算的SAS程序代码

53 proc freq data=par;54-56 table factor4*case/chisq;run;data list_5;57 set list_1 list_2 list_3 list_4;58 keep factor1 factor2 factor3 factor4 case Frequency sum_1;59 if case=1;/sle=0.5 sls=0.5 noint; 60 if factor1^=.or factor2^=.or factor3^=.or factor4^=.;12 proc print data=test NOOBS; 61-62 sum_1=103;proc sort;13 title＇数学模型统计学检验＇; 63-65 by factor1;data list_6;set list_1 list_2 list_3 list_4;14-15 ods listing;data t; 66 keep factor1 frequency control;16 set test; 67 if case=0;17 if test= ＇Likelihood Ratio＇; 68 if factor1^= .or factor2^= .or factor3^= .or factor4^= .;18-19 title＇数学模型统计学检验结果提示＇;file print; 69-70 data list_7;set list_6;20 if Prob_ChiSq ＜0.05 then put//+30 ＇结果提示：数学模型检验显示有统计学意义!＇;71-73 rename frequency=control;proc sort;by factor1;21 else put//+30＇结果提示：数学模型检验显示无统计学意义!＇;74-75 data list_all;merge list_5 list_7;22-23 data OR_EST;merge EST OR; 76-80 by factor1;data calcu_1;set list_all;if factor1^=.;class=put(factor1，$1.);24 if effect= ＇factor1＇or effect= ＇factor2＇or effect= ＇factor3＇or effect= ＇factor4 ＇;81-84 data calcu_11;set or_est_1;rename ClassVal0=class;if variable= ＇factor1＇;25 DROP EFFECT DF; 85 data calcu_111;26 PROC PRINT NOOBS; 86 merge calcu_1 calcu_11;27 title＇宁波口岸某病风险因素及风险度＇; 87 by class;28 RUN;ods listing close; 88 if class= ＇1＇then oddsRatioEst=1;29 ods output OddsRatios=OR_1; 89 parc=Frequency/sum_1/oddsRatioEst;30 ods output ParameterEstimates=est_1; 90 ods output Summary=summy;31 ods output GlobalTests=test_1; 91 proc means sum data=calcu_111;32 proc logistic descending data=par; 92-94 var parc;data a;set summy;33 class factor1(ref=first)factor2(ref=first)factor3(ref=first)factor4(ref=first)/param=ref;95-96 parc_1=abs(1-parc_Sum)*100;data calcu_1111;34 model case=sex address age factor1 factor2 factor3 factor4/sle=0.5 sls=0.5 noint;97 merge calcu_111 a;35 data OR_EST_1; 98 keep factor1 frequency control oddsRatioEst parc_1;36 merge EST_1 OR_1; 99 data calcu_11111;37 if effect^= ＇sex＇and effect^= ＇address＇and effect^= ＇age＇; 100 set calcu_1111;38 DROP EFFECT DF; 101 rename frequency=case;39 ods listing close; 102-103 ods listing;PROC PRINT noobs;40 ods output CrossTabFreqs=list_1; 104 itle＇宁波口岸某病风险因素A的调整人群归因危险度(PARc%)＇;41 proc freq data=par; 105-106 RUN;quit;

5 讨论

人群归因危险度的计算相对比较简单，但在自然现象中，往往有混杂因素或是多个因素同时存在，则单因素人群归因危险度计算公式就不再适用，而须计算调整控制一个或多个变量后的PAR指标［4］。国外有学者曾提出用Mantel-Haenszel法、非条件法、加权合并法及基于回归模型的调整估计法等方法来调整多个干扰因子的效应。但笔者认为，以基于回归模型的调整估计法为优，主要考虑以下几点因素：①基于回归模型的调整估计法允许控制调整较多的混杂和效应修正因子;②混杂项、交互项均较易于直接加入模型方程中;③参数估计和假设检验灵活方便。

本研究正是采用Bruzzi提出的基于回归模型的调整估计法，其原理不是直接拟合PAR模型，而是把基于回归模型的调整的RR估计加入到PAR估计中去。Bruzzi认为，如果病例对照资料的病例是随机样本，用Logistic回归模型估计诸危险因素与传染性疾病的相对危险度后，即可经病例的暴露分布求出PAR。本研究的病例为宁波口岸某病全年所有的病例人群，故与Bruzzi提出的确定病例人群的条件并不矛盾，因此亦可直接应用。Bruzzi法的优点是仅需知道病例的暴露分布而不需人群暴露状况，即可估计危险因素不同水平的PAR值。

由于整个运算过程比较繁杂，计算工作量较大，且靠手工计算容易出错。为此，本研究应用国际权威的统计分析标准软件——SAS分析平台进行编程［5］，还在程序中设定了一些自动判断过程，实现了多因素影响的口岸流行病风险因素调整人群归因危险度的全自动计算机运算，这在国内相关研究中尚属首次。所得结果经过了手工计算及SPSS软件半自动运算的双重验证，证明准确可靠，为口岸流行病发生与控制效果的评价提供了一种简便快捷且客观有效的评估工具。

［1］Rebecca J Guy，Handan Wand，David P Wilson，et al.Using population attributable risk to choose HIV prevention strategies in men who have sex with men ［J］.BMC Public Health，2011，11：247.

［2］Giovanni de Simone，Jorge R.Kizer，Marcello Chinali，et al.Normalization for body size and population-attributable risk of left ventricular hypertrophy［J］.Am J Hypertens，2005，18：191-196.

［3］Wendy Y Chen，Bernard Rosner，Susan E Hankinson，et al.Moderate Alcohol Consumption During Adult Life，Drinking Patterns，and Breast Cancer Risk［J］.JAMA，2011，306(17)：1884-1890.

［4］沈月平，武俊青，高尔生.隐函数Delta法调整人群归因危险度可信区间的估计及其应用［J］.中国卫生统计，2004，21(3)：142-145.

［5］高惠璇，译.SAS系统SAS/STAT软件、BASE SAS软件使用手册［M］.北京：中国统计出版社，1997，1-30.