T700复合材料层合板拉-拉疲劳性能

王 军， 程小全， 张纪奎， 郦正能

（北京航空航天大学航空科学与工程学院，北京 100191）

由于具有优越的力学性能，复合材料在现代航空航天结构上得到了广泛的应用，并且越来越多的应用于飞行器的主承力结构。国际上最新型的大型客机B-787和A350上，复合材料占全机结构比重已经超过了50%。结构材料的疲劳性能，对飞机的可靠性和安全性起着决定性影响，因此复合材料疲劳性能方面的研究对于保证飞机的安全和提高飞机使用寿命具有重要的意义。但相对于金属，复合材料结构的复杂性使其对其损伤机理和损伤扩展机制的研究都要复杂困难的多。

从20世纪70年代末开始，国内外研究人员开展了一系列对于复合材料疲劳方面的研究，取得了大量的研究成果［1～10］。其中，对于目前较为成熟的T300型碳纤维增强复合材料的疲劳性能的实验和寿命预测研究开展较多，取得了很多有应用价值的成果。近年来，T700新型纤维增强复合材料得到了日益增多的应用，相对于T300纤维，T700以其更好的加工工艺得到的更优秀的拉伸强度，正逐渐开始替代T300纤维。但对T700碳纤复合材料的疲劳性能方面的研究，目前仍然还较为缺乏。

本研究对T700/9368复合材料试件进行了拉-拉疲劳试验，对试件刚度衰减和疲劳损伤扩展进行了初步研究，并建立了疲劳损伤模型，对试件的疲劳寿命进行了预测。

1 试验

1.1 试件

试验件均为T700/9368层合板，试验件的设计参考了《聚合物基复合材料手册》［11］及相关的试验标准。试件分为三组，光滑板和两种不同孔径的含孔层合板各1组，两端均粘贴50mm长加强片加固。试件几何形状及尺寸见表1和图1所示。全部试件的铺层均为20层 T700/9368，铺设顺序均为［45/90/-45/0/45/0/-45/0/90/0］s，（45°铺层比例为40%。

表1 试验件尺寸表Table 1 geometry of specimens

1.2 试件设备与方案

拉-拉疲劳试验在INSTRON8802材料试验机上进行，试验按照HB5440—1989（碳纤维树脂基复合材料拉-拉疲劳试验方法［11］）标准。试验环境条件为自然干态（常态），环境温度为（23±3）℃。

对三组试件分别先进行静载拉伸试验，得到每组试件的拉伸强度，用以确定疲劳试验所需的载荷。

图1 疲劳试验件Fig.1 specimens for fatigue test （a）smooth Iaminate;（b）laminate with a hole

表2 各组试件拉伸强度Table 2 tensile strength of specimens

1.3 光滑板试验

1组光滑板拉-拉疲劳试验加载方式为正弦波，加载频率10Hz，应力比均为0.1，引伸计跨距为130mm。一定循环次数后，通过材料试验机所带的应变引伸计测量各试件应变，获得试件的刚度变化状况。试件内部损伤采用超声C扫描技术检测。

1组光滑板试验共选择70%、65%和60%三个应力水平，前两个应力水平各取3个试件，60%应力水平取1个试件。

各试件疲劳寿命见表3。从表中可以看出，除T700-KF1-3试件结果明显偏离被去掉外，每个应力水平的光滑板疲劳寿命分散性均较小，试验具有较好的置信度。由于T700碳纤维相比T300碳纤维的延伸率较大，因而出现大规模的纤维断裂时间点较迟且偏差小，这也是T700层合板比T300层合板疲劳寿命分散性小的原因之一。

表3 光滑板疲劳试验寿命Table 3 Fatigue life of smooth laminates

图2为70%和65%应力水平的试件刚度随循环次数的衰减曲线。E0为初始刚渡，En为循环n次后剩余刚渡;N为疲劳寿命。从图2中可以看出，疲劳加载的初始阶段，刚度衰减比较剧烈，当循环次数超过10%寿命后，刚度衰减稳定近似为一条直线（70%应力水平下循环次数在97%全寿命点刚度明显下偏，是因为此时已经进入了快速扩展区间）。

从图2中还可以看出，应力水平在65%和70%两种情况下，全寿命范围内试件的刚度衰减曲线相似度极好，而且具有在较长的疲劳加载段刚度的线性变化的特点，使得本工作后面以刚度降作为损伤量模拟的疲劳模型成为可能。

试件拉-拉疲劳破坏情况如图3所示。可以看出，T700层合板试件拉-拉疲劳的主要破坏特征是出现了大面积分层，这与静态拉伸试件只在断口处有分层明显不同。相比T300层合板，T700层合板疲劳破坏后的试件分层面积更大，分布更密，这一方面是因为T700碳纤维的延伸率好，纤维断裂出现迟;另一方面，T700的表面质量相比T300更光滑，树脂与纤维界面强度有所下降。

图2 光滑板的刚度衰减曲线Fig.2 Stiffness attenuation curve of smooth lamiates

图3 光滑板的拉-拉疲劳破坏Fig.3 Tension-tension fatigue failure of smooth laminate

对60%应力水平的T700-KF3-1试件在不同循环次数下进行了C扫描无损检测，如图4所示。结果表明，在疲劳加载初始阶段，层合板内部即出现明显的分层损伤。这时的循环次数只占层合板疲劳寿命的极小一部分，而且随着循环次数的增加，首先是在两端及边缘部位出现分层，然后向中间迅速扩展，伴随着45°方向的分布式基体开裂，在较短的时间里就出现大面积的分层，到30000次循环即约10%疲劳寿命时，分层已经接近扩展到整个层板，这也导致了图2中疲劳加载初始阶段刚度迅速下降。此阶段力学性能上表现出的刚度衰减，主要来自于初始阶段分层损伤和基体开裂。

经过此阶段后，分层损伤已经达到一个稳定扩展阶段，刚度衰减如图2所示接近为直线，直到接近90%寿命后出现大面积纤维断裂导致板破坏。此结论和文献［10］相一致。

图4 光滑板拉-拉疲劳试验C扫描结果Fig.4 C-scan result of smooth laminate after tension-tension fatigue test（a）1000 cycles;（b）10000 cycles;（c）30000 cycles

1.4 含孔层合板拉-拉疲劳试验

2组和3组含孔板试件拉-拉疲劳试验加载方式为正弦波，加载频率10Hz，应力比为0.1，引伸计跨距为200mm。对两种孔径的试件选择不同的应力水平进行拉-拉疲劳试验。

含孔层合板试验共选择90%、85%和80%三个应力水平，前两个应力水平各取3个试件，80%应力水平取1个试件。

各试件疲劳寿命见表4。可以看出，除T700-KT1-3试件结果明显偏离外，三个应力水平的光滑层合板疲劳寿命分散性较小，试验具有较好的置信度。

表4 含孔层合板疲劳试验寿命Table 4 Fatigue lives of laminates with holes

含孔层合板试件拉-拉疲劳破坏情况如图5所示。试件断口位置大致与静态拉伸试件相同，位于孔两侧，但分层面积要大的多。

图5 含孔板的拉-拉疲劳破坏Fig.5 Tension-tension fatigue failure of laminate with a hole

对试件T700-KT2-2在不同循环次数下进行了C扫描无损检测，结果如图6所示。孔板内部初始损伤出现得很早，随着循环次数的增加，先是在试件中段圆孔附近出现分层损伤，然后迅速由孔边向两端沿45°纵向扩展，在较短的时间里就出现大面积的分层，在经历长时间的疲劳载荷作用后，最后在试件中间圆孔部位断裂破坏。

2 疲劳损伤模型

2.1 光滑板疲劳损伤模型

对复合材料疲劳寿命预测的疲劳累积损伤理论是运用固体物理学、材料强度理论和连续介质力学的唯像方法，它以材料的表观现象为依据，建立与损伤耦合的力学分析模型，通过力学和数学的分析与计算，获得所需的数值结果。

图6 孔板拉-拉疲劳试验C扫描结果Fig.6 C-scan result of laminate with a hole after tension-tension fatigue test（a）5000 cycles;（b）8000 cycles;（c）12000 cycles

在试验阶段用于复合材料的疲劳寿命预测的模型，包括剩余强度模型［1］、剩余刚度模型［2～6］以及耗散能模型［7］等等。本文在实验研究所得到的刚度衰减结果基础上，建立了剩余刚度模型，对T700/9368层合板寿命进行预测。

Lemaitre［8］创立的应变等效性假说认为，应力作用于受损材料所引起的变形等效于作用于一虚拟的无损伤材料的变形，虚拟无损伤材料的承载面积等于受损伤材料的实际有效承载面积。对于一维问题，该原理可用公式表示为:

此式即为弹性模量法即刚度下降法定义和度量损伤的基本依据。其中:D为损伤变量;E'为受损材料的损伤模量;E为无损材料的损伤模量。

由此可以根据材料受损前后弹性模量的衰变来确定损伤的大小。为了把式（1）中定义的损伤因子应用到复合材料层合板的疲劳过程中，则应将损伤因子D和循环次数n建立起函数关系。

以往研究结果［9］和本次的实验结果均表明，纤维增强复合材料的疲劳损伤过程往往呈现出两个明显不同的阶段，第一阶段损伤扩展比较平稳，占总疲劳寿命的90%左右，而当疲劳损伤达到一定的程度后会进入第二个阶段，这时候损伤发展比前一个阶段快得多，在很短的时间内材料就发生破坏。因此本工作考虑采用分段函数对这两个过程分别进行构建。第一阶段损伤函数D1用指数函数构建，第二阶段损伤函数D2用线性函数构建。

Beaumont［7］根据对横向裂纹扩展的分析提出第一阶段疲劳损伤函数D1的表达式:

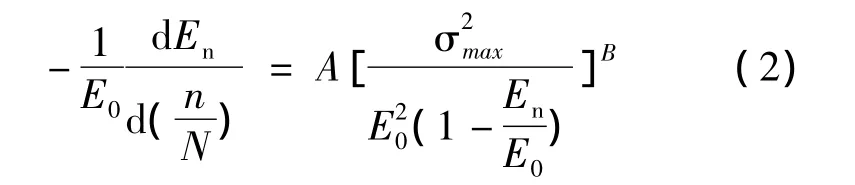
式中A，B为材料常数;σmax为材料受到的最大循环应力。

对式（2）积分，且令:

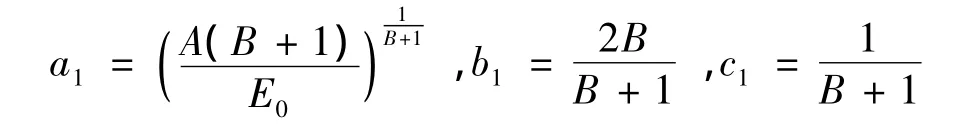
其中a1，b1，c1为材料常数。

即可得到第一阶段损伤扩展模型:

式中a2，b2，c2为材料常数。

取第一阶段和第二阶段的分界循环次数为nc，即当0≤n≤nc时，D=D1;当nc≤n≤N时，D=D2。nc可以根据试验测得的刚度衰减数据和多元最小二乘法进行求解。

2.2 含孔层合板疲劳损伤模型

对于带中心孔的层合板，在任意拉伸载荷作用下，只要求得特征长度a0之内的平均应力σy，加上一个修正系数β相乘来替换前面光滑板损伤模型式中的σmax，即可得到含孔板的疲劳累积损伤模型:

第二阶段占疲劳总寿命时间很短，D2可用线性函数构建:

式中β可以通过孔板拉伸疲劳试验确定。得到β值后则可以由此模型预测含孔板的拉伸疲劳寿命。

3 疲劳寿命预测

3.1 光滑板疲劳寿命预测

将T700/9368层合板70%和65%应力水平下试验结果对层合板疲劳损伤模型进行参数拟合。

应用最小二乘法可得到拟合系数:a1=2.43×10-14，b1=-6.88，c1=0.33，a2=-553.5，b2=44035。

将拟合系数代入式（3）和（4）得到T700/9368层合板疲劳损伤模型表达式为:

本工作的计算和实验结果均表明，当层合板弹性模量下降的初始模量的70%左右时，出现疲劳损伤分界点，循环次数约占总疲劳寿命的90%，见表5。

表5 损伤分界点Table 5 Damage turning point

运用此模型对60%应力水平下的T700/9368层合板疲劳寿命进行预测。结果如表6所示。

表6 60%应力水平的疲劳寿命预测结果Table 6 Fatigue Life Predication results at 60%stress level

3.2 含孔层合板疲劳寿命预测

将孔板静态拉伸试验测得的试验数据结合层合板性能参数，即可得到孔板特征长度，结合孔板拉-拉疲劳试验，即可得到修正系数 β的值，见表7。

表7 不同孔径试件β计算值Table 7 β calculating results for specimens with a hole of different diameter

将β值代入式5，即可得到T700/9368含孔板疲劳损伤模型表达式为:

运用此模型对T700-KF2-1孔板拉伸疲劳试件疲劳寿命进行预测，并与试验结果比较，结果见表8。

表8 T700-KF2-1孔板寿命预测值Table 8 Fatigue Life Predication result of specimen T700-KF2-1

4 结论

（1）在疲劳载荷作用下，光滑板损伤从边缘开始，含孔板损伤从孔边开始，在初始阶段分层扩展迅速，并伴随45°方向的基体开裂，到疲劳寿命的10%前，试件的刚度衰减较快。

（2）在疲劳寿命的10%到90%范围内，试件的剩余刚度随加载周期基本以线性规律下降，损伤表现为分层扩展。

（3）到达90%疲劳寿命时，试件刚度约降至初始刚度的70%，此时开始出现大面积纤维断裂，试件迅速破坏。

（4）与静拉伸试件断口相比，疲劳试件表现出覆盖全试件的大面积分层，光滑板断口出现在试件中部;含孔板和静拉伸断口均出现在孔边。

（5）与T300碳纤维相比，T700纤维的延伸率较大，使得T700层合板的疲劳寿命分散性较小，有利于对疲劳寿命准确预测;同时由于T700纤维表面更光滑，与树脂界面性能有所下降，断裂后试件的分层和劈丝更加明显。

（6）利用部分试验结果确定疲劳模型的参数，对T700/9368试件的寿命进行了预测，预测结果吻合良好。

［1］RADHAKRISHNAN K.Fatigue and reliability evaluation of unnotched carbon epoxy laminates［J］.Comp Mat，1984，10（1）:21-31.

［2］YANG J N.Residual strength degradation model and theory of periodic proof tests for graphite pepoxy laminates ［J］.Journal of Composite Materials，1977，11（4）:177-197.

［3］STINCHCOMB.Nondestructive evaluation of damage accumulation processes in composite laminates［J］.Comp Sci＆ Tech，1986（25）:103-118.

［4］PAUL.A damage accumulation in graphite/epoxy laminates due to cycilc gradient stress fields［J］.Rein.Plas ＆Comp，1993，12（10）:111-116.

［5］齐红宇，温卫东.先进纤维增强复合材料疲劳寿命的预测［J］，纤维复合材料，2001，2（3）:3-6.

QI Hong-yu，WEN Wei-dong.Prediction of Fatigue Life of Advanced Fiber Reinforced Maerials［J］.Fiber Composites，2001，2（3）:3-6.

［6］齐红宇，温卫东，崔海涛.含孔复合材料层合板疲劳寿命预测研究［J］.航空动力学报，2003，18（5）:658-661.

（QI Hong-yu，WEN Wei-dong，CUI Hai-tao.Fatigue Life Predication of Notched Composite Material Laminates.Journal of Aerospace Power［J］，2003，18（5）:658-661.）

［7］BADALIANE R，DILL H D.Damage in composite materials［J］.ASTM STP775，1982，（6）:229.

［8］LEMAITRE J.Evolution of dissipation and damage in metals，submitted it dynamic loading［C］.Proc.I.C.M.I，Kyoto.Japan 1968.

［9］程光旭.复合材料疲劳损伤演化两阶段模型［J］.机械工程材料，2000，24（4）:7-10.

（CHENG Guang-xu，WEI Wei，LI Guang-ze.A General Two stage model for accumulation of fatigue damage in composite materials［J］.Materials for Mechanical Engineering.2000，24（4）:7-10.）

［10］徐颖，温卫东，崔海坡.含冲击损伤复合材料层合板疲劳试验研究［J］.宇航材料工艺，2007，（12）:73-80.

（XU Ying，WEN Wei-dong，CUI Hai-po.Fatigue testing of impact-damaged composite laminates［J］.Aerospace Materials＆ Technology.2007，（12）:73-80.）

［11］陈祥宝.聚合物基复合材料手册［M］.北京:化学工业出版社，2004:54-56，73.

［12］杨光松.损伤力学与复合材料损伤［M］.北京:国防工业出版社，1995:132-135.