散体桩复合地基固结有限元网格划分效应分析＊

邓岳保，谢康和，王 坤

（浙江大学 软弱土与环境土工教育部重点实验室，浙江 杭州 310058）

散体桩复合地基目前应用广泛，该项技术的一个重要课题是研究其排水固结效应[1－2］.由于要考虑桩体的应力集中，散体桩复合地基固结分析无论是解析解还是数值解，均要落后于竖井地基研究[3－4］.在应用有限元分析散体桩复合地基固结方面，途径之一是先用解析方法计算固结，用数值方法计算变形与应力，然后通过两者结合以解决复合地基变形随时间发展的问题[2］.该法建立于Terzaghi固结理论基础之上，在求解效率上有优势，但不够严密.更多学者致力于用严密的Biot固结理论进行分析.

朱百里、沈珠江对早年研究者在Biot固结有限元方面所作研究进行了汇总[5］.徐洋则对上世纪国内外学者应用有限元分析散体桩复合地基进行了综述[6］.陈祖煜采用基于Biot固结理论的二维平面应变程序对碎石桩加固坝基的应力应变与固结过程进行了预测和分析[7］.邢皓枫针对某电厂碎石桩复合地基现场试验测试成果进行有限元法模拟[8］.Kim＆Park将挤密砂砾桩单桩影响范围等效为圆柱体，然后进行非线性有限元分析[9］.傅少君等在分析振冲碎石桩变形和受力机制的基础上，结合弹性力学和Biot固结理论建立了平面有限元分析弹性复合模型[10］.另外，崔溦应用Plaxis对土工格栅＋碎石桩复合地基进行了分析[11］.

汇总上述国内外文献可见，相对于不考虑时间效应的有限元分析，散体桩复合地基固结有限元研究还不够深入.将Biot理论应用于复合地基有限元分析的基础性研究，如单元形态、形函数选取与时间步长等对数值结果的影响，已有文献较少涉及.为此，本文将开展散体桩复合地基网格效应研究.

1 分析条件

1.1 有限元程序

由于解析方法能力有限，并考虑到竖井地基固结问题的空间属性，谢康和编制了基于Biot固结理论的“平面变形、空间渗流”程序和“空间变形、空间渗流”程序[12－13］.之后，徐洋和本文作者对其进行了进一步扩充与完善.目前，该系列程序主要功能如下：

1）可分析天然地基、竖井地基或复合地基的变形与固结；2）可进行一维、平面应变、轴对称和三维问题分析；3）材料本构模型可选择线弹性、邓肯－张非线性弹性、XKH非线性模型和修正剑桥模型；4）可考虑刚性基础（筏板）、柔性基础（路堤）及路堤中有土工织物等情况；5）可分析土层超固结状态、地下水位及土层倾斜等影响；6）可分析施工扰动影响，即可以考虑涂抹区渗透系数和压缩系数与未扰动区的差异情况；7）可分析非对称荷载（如反压互道）对固结计算的影响.

数值解法及其程序的验证是岩土工程问题有限元分析中的重要环节，上述程序的验证工作可分为如下两方面：一是与解析解对比，包括一维固结解析解、单井固结解析解、单桩复合地基固结解析解、天然地基在矩形荷载和圆形荷载作用下的弹性解等.二是与现场实测数据对比，包括上海宝钢原料堆场砂井地基大型堆载试验、宁波机场袋装砂井地基超载预压试验以及宁通公路二灰土桩复合地基分析等.近年来，该程序还在一系列工程中得到应用.

1.2 物理模型与边界条件

将散体桩圆截面等效为同面积的正方形，并取单桩影响范围内的方形地基进行分析，如图1（a）.图中虚线所围面积abcd即为等效后的单桩地基.经过该处理后，地基横截面边长为ds，桩横截面边长为dp.根据面积等效原则，桩径dw、单桩圆柱体等效地基的直径de与dp、ds之间有如下转换关系[12］：

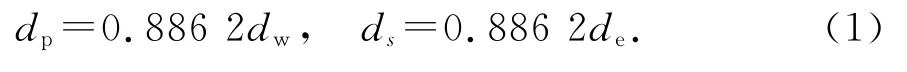
有限元分析坐标系统及空间网格划分见图1（b）.图中Δp，Δs和Δz分别为桩横截面网格尺寸、桩周土体横截面网格尺寸和地基深度方向网格尺寸.单桩地基几何尺寸如下：ds＝1.6m；dp＝0.4 m；地基深度方向厚度H＝10.0m，散体桩穿透软弱土层.

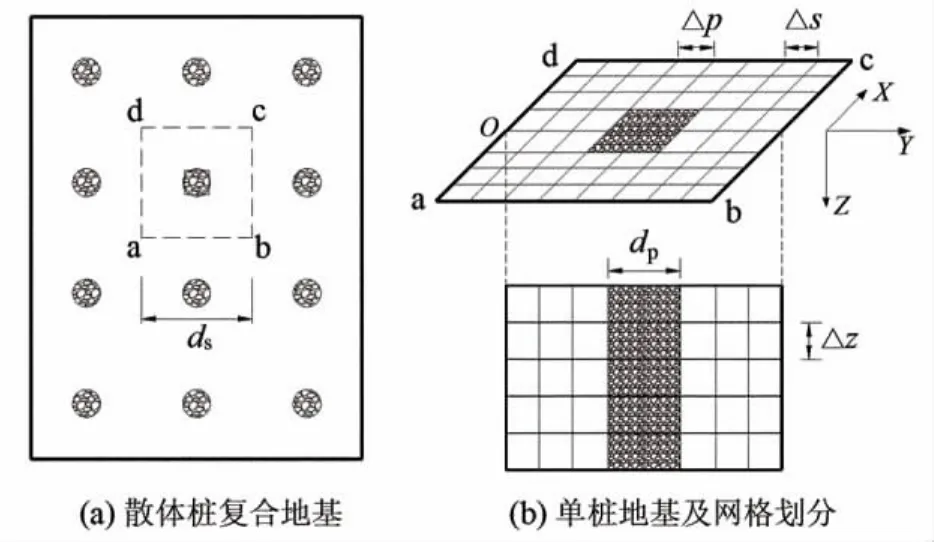
图1 物理模型Fig.1 Calculation model

为与解析解进行对比，桩及地基土体均假定为各向同性线弹性材料，其渗透特性亦假定为各向同性，相应的物理力学参数取值见表1.另外假定地基上荷载q0瞬时施加，其值取30kPa.根据式（2）亦可获得桩体压缩模量Eps值.

表1 地基物理力学参数取值Tab.1 Value of physical and mechanical parameters

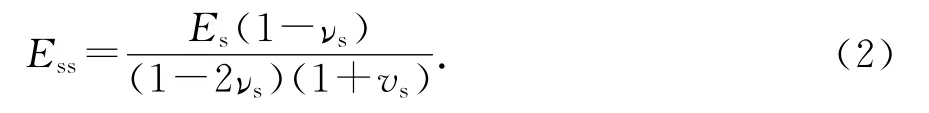
边界条件：排水边界为顶层透水、底层及四周不透水；位移边界为顶层自由，底层约束，四周仅深度方向自由.

1.3 解析解答

为分析不同网格划分带来的误差，根据上文计算模型，选用卢萌盟（2009）解析解作为参考[4］.该解答在假定桩无侧向变形的基础上考虑了复合地基应力集中效应及桩内径、竖向渗流组合的影响，是目前与本文分析对象最接近的闭合解答.当不考虑涂抹效应且桩土材料各项同性时，求解公式简化为：土体压缩模量Ess与表中弹性模量转换关系为：

1.4 有限元分析网格划分工况

分7种工况进行对比分析，如表2所示.

表2 计算工况Tab.2 Analysis conditions

1.5 有限元分析时步选取

当网格确定后，时间步长Δt选取非常重要.Δt太小会导致刚度矩阵的病态，太大会使结果误差增大.目前估算时步的方法有两种[5，14］，分别为：

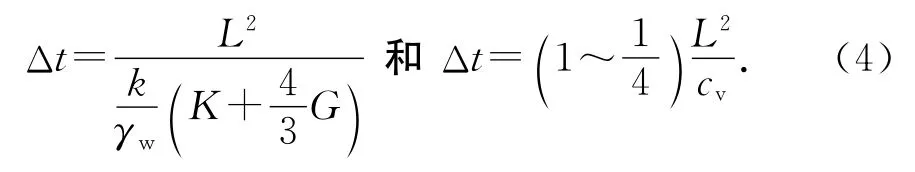
对式（4）有如下几点不加推导的说明：1）两式用于时步分析时均能反映网格和固结系数的影响，相对来说后式应用更简单.2）式中系数范围1～1/4由土体泊松比决定.式中L为近排水面处的网格尺寸，对于竖井地基或散体桩复合地基而言，主要指桩（井）周土体径向网格尺寸.3）时步选取除与网格划分和固结系数有关外，还与固结时间和荷载增量有关.当地基中孔压梯度和变形梯度减小时，时步可取较大值.但在荷载突跳处，时步选取要满足式（4）.

据前文网格划分并结合式（4），取初始时步Δt＝0.5d.总固结时间取45d，时步总数为15级，详细划分情况可参考后文固结度计算结果图.

2 网格划分效应分析

2.1 地基竖向网格划分的影响

复合地基深度方向上，工况1，6和7网格划分尺寸分别为0.5m，1.0m 和2.0m，水平面内网格划分尺寸相同.3种工况下固结度计算结果与解析解对比情况见图2.由图可知：深度方向3种网格划分得到的结果非常接近，但与解析解均有一定误差；网格划分越密（工况1），数值解越趋近于解析解.

图3为时步step＝5和step＝10时3种工况地基深度z＝2.0m处超静孔压结果对比.图中纵坐

图2 地基竖向网格尺寸对固结度结果影响Fig.2 Effect of vertical grid size on consolidation degree

标为超静孔压p与荷载q0的比值.由图可知：相对于固结度误差情况，网格划分对孔压结果带来的误差要明显；随着时间的发展，孔压逐渐消散，step10的误差较step5的误差减小.

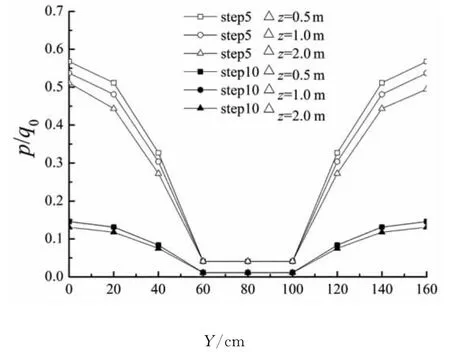
图3 竖向网格尺寸对孔压的影响（z＝2.0m）Fig.3 Effect of vertical grid size on pore pressure（z＝2.0m）

为对比不同深度处误差情况，图4给出了step＝5时地基深度z＝6.0m处超静孔压结果.由图可得，工况1，6得到的孔压解接近，工况7（网格划分较疏）孔压结果与上述解有一定误差，但误差较小.结合图3和图4可知：相同时刻，在地基浅层处（近顶层透水面）网格划分带来的超静孔压误差较地基深层处大.

由此可得，深度方向的不同网格划分对固结度计算结果影响较小，对孔压计算结果影响相对明显，但总体上也较小.地基深层处孔压误差要小于地基浅层近排水面处误差.随着时间发展，深度方向网格划分带来的误差进一步减小.

2.2 桩周土横截面网格划分的影响

桩周土体横截面内网格划分尺寸分别为0.1 m，0.2m和0.3m，3种计算工况下固结度计算结果与解析解对比情况见图5.

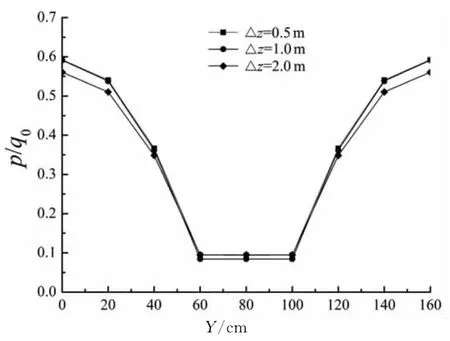
图4 地基竖向网格尺寸对孔压的影响（z＝6.0m）Fig.4 Effect of vertical grid size on pore pressure（z＝6.0m）

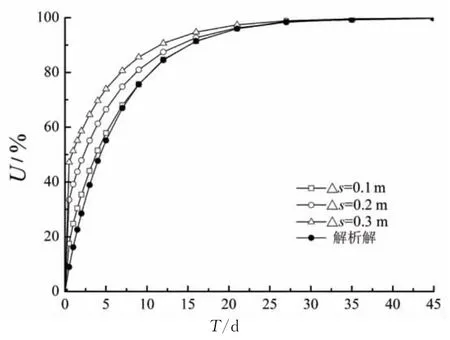
图5 土体平面网格尺寸对固结度结果影响Fig.5 Soil surface mesh size effect on consolidation degree

由图5可看出：1）桩周土横截面三种网格划分得到的计算结果相差较大，表明地基土体平面网格划分对固结计算结果影响显著；2）桩周土截面网格划分越密，地基固结速率越慢，计算结果越趋近于解析解.

地基深度z＝2.0m和6.0m处，桩周土体横截面不同网格划分的超静孔压结果对比见图6和图7.由图可知，三者结果相差较大，即桩横截面不同网格划分对超静孔压影响显著；不同深度处孔压误差均较明显.另外，随着时间发展，孔压误差呈减小趋势.

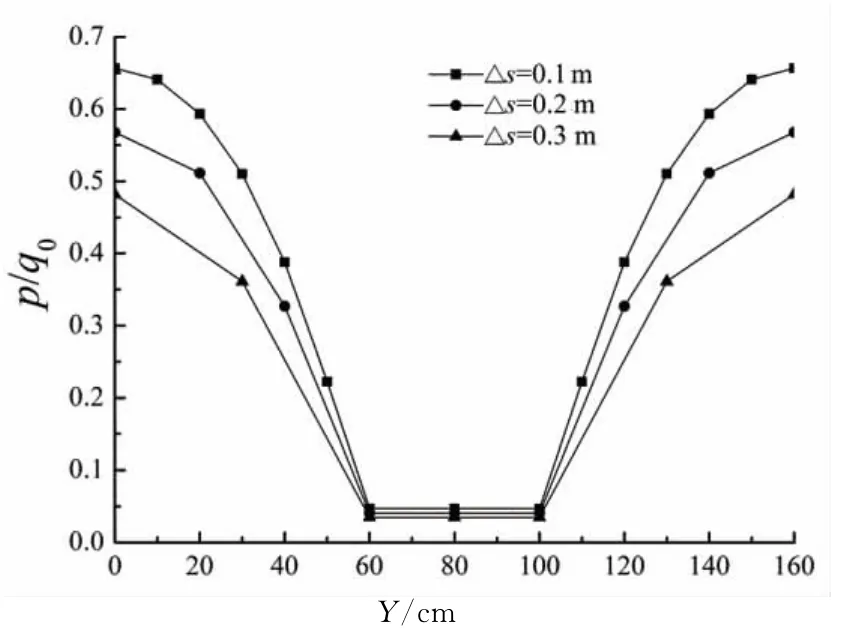
图6 土体平面网格尺寸对孔压影响（z＝2.0m）Fig.6 Soil surface mesh size effect on pore pressure（z＝2.0m）

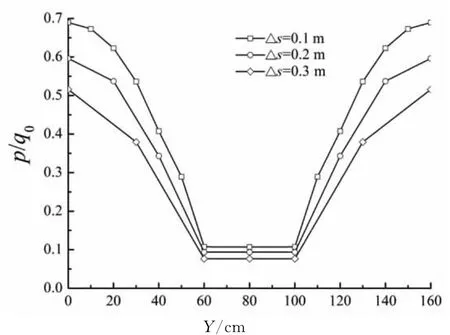
图7 土体平面网格尺寸对孔压影响（z＝6.0m）Fig.7 Soil surface mesh size effect on pore pressure（z＝6.0m）

由此可得，桩周土体平面网格划分对固结度和孔压计算结果影响均非常明显，土体平面网格细分能得到与解析解接近的解答.

2.3 桩横截面网格划分的影响

散体桩横截面网格划分尺寸分别为0.1m，0.2 m和0.4m，其平面网格数分别为16，4和1.3种工况下固结度计算结果与解析解对比情况见图8.

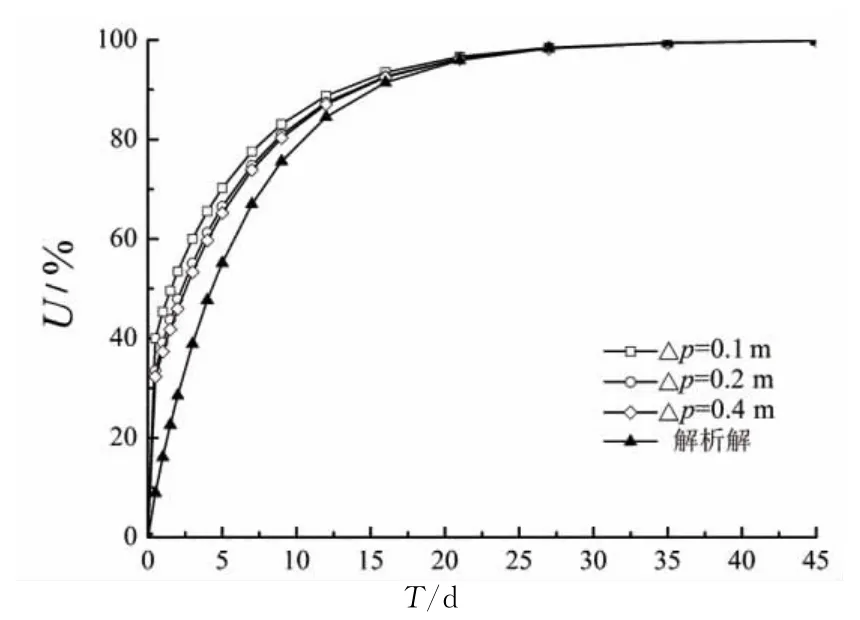
图8 桩截面网格划分对固结度结果影响Fig.8 Effect of pile section mesh size on consolidation degree

由图可知：1）桩截面3种网格划分的计算结果接近，表明桩截面网格划分对固结度计算结果影响不明显；2）由于散体桩固结速率大，随着桩截面网格数增加，桩体固结占地基整体固结的比重增大，从而使得总体固结度计算值增大，但影响不显著.

地基深度z＝2.0m处超静孔压结果对比见图9.由图可知，三者孔压结果相差很小，表明桩横截面的不同网格划分对超静孔压影响不明显.

2.4 固结计算误差总体分析

以解析解为基准，分析各工况相对误差大小，其结果如图10所示.图中，相对误差Er＝（U1－U）/U，U为解析解答，U1为数值解答.

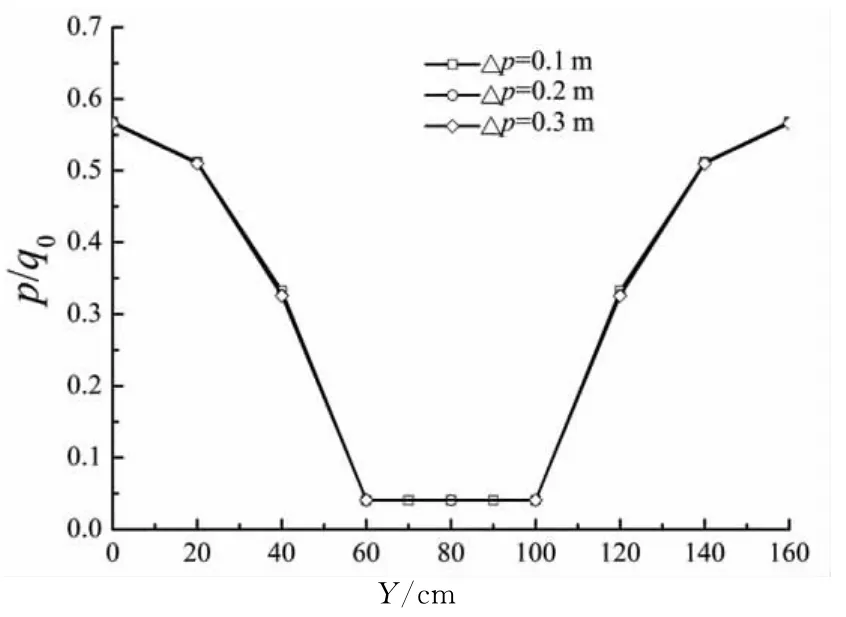
图9 桩截面网格划分对孔压影响Fig.9 Effect of pile section mesh size on pore pressure

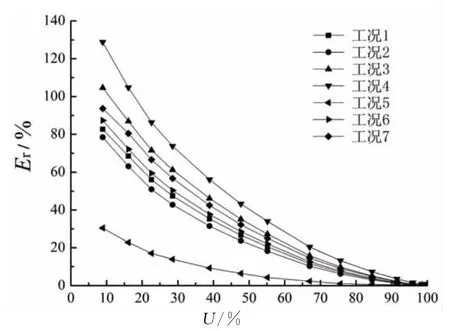
图10 各计算工况误差对比Fig.10 Error comparison of various calculation condition

由图可见：1）随着固结度增大，各工况得到的误差均减小，且减小趋势随固结度增大而减缓；2）当固结度为50%时，各工况误差均在50%以内，当固结度达70%时，网格划分带来的误差减小到20%以内.3）各计算工况误差对比中，工况4和工况5分别为误差最大和误差最小的两条曲线，表明桩周土体横截面网格划分的影响最为显著，此即网格误差主要来源.其余各工况得到的曲线相隔较小，表明桩截面网格划分及地基深度方向网格划分影响相对前者不显著.

汇总超静孔压误差可知，网格划分带来的孔压误差与固结度误差不一致.前者除具有时间性外还具有空间性，即孔压误差在水平面内和地基不同深度处均有差异.排水面越近处孔压梯度变化越明显，网格划分误差越明显.

2.5 网格划分效应讨论

1）散体桩复合地基中，桩渗透性远大于土体渗透性，故在近似分析中可将桩假设为完全透水材料，如文献[11］.由此，不管桩的网格划分如何，桩内超静孔压均接近零，故桩截面网格划分对固结计算影响不显著.平面内桩体只要有一个网格存在，桩体就能起到排水通道的作用.

2）由于排水桩的存在，复合地基中土体渗流以径向为主.桩周土体在近桩处临近透水面，超静孔压接近零，而单桩复合地基外围为不透水面，超静孔压相对难以消散.在该较小的径向距离内，孔压梯度变化非常明显，孔压分布呈现显著的非线性.若网格数过少，则不能反映桩周土体上述径向排水的非线性性状，由此可解释桩周土体水平面内粗略的网格划分会引起较大误差的原因.根据本文计算发现，桩与桩之间土体需要设置6排以上的单元.

3）地基浅层处孔压误差相对深处显著，原因之一是浅层处接近地基顶层透水面，其二是桩体的鼓胀效应.据以往散体桩实测数据和有限元侧向位移结果，均可得散体桩鼓胀效应的存在，且该效应主要发生在地基浅层处（通常在4倍桩径深度以内）.由此可知浅层处地基土体体积变化较地基深层处明显.根据Biot固结理论中的渗流连续方程，可知该处的流体流速变化剧烈，即孔压梯度变化显著，这样可解释孔压在地基浅层处较深层处误差明显.

4）根据固结理论，固结度反应整个地基的固结程度，为各节点固结性状的平均，而超静孔压反映的是地基中任意点处的固结情况，所以固结度误差与孔压误差不一致，且孔压误差具有空间属性.

3 结 语

1）桩周土体横截面网格尺寸是有限元网格划分引起误差的主要原因，网格划分数需要6排以上才能合理反映桩周土体径向渗流的非线性；

2）桩截面网格划分对固结计算影响不明显，平面内散体材料桩的排水效应可用一个网格刻画；

3）地基深度方向的网格尺寸在一定范围内变化时，固结度计算结果变化很小，但要得到精度较高的超静孔压结果，需在近排水面和桩体鼓胀效应明显的地方细分网格.

[1]ZHANG Ling，ZHAO Ming－hua，ZHAO Heng.Time effect on bearing capacity of composite foundation with stone columns[C］//GeoHunan International Conference，Changsha：ASCE，2009：183－188.

[2]张爱军，谢定义.复合地基三维数值分析[M］.北京：科学出版社，2004：49－50.ZHANG Ai－jun，XIE Ding－yi.Three dimensional analysis of composite foundation[M］.Beijing：Science Press，2004：49－50.（In Chinese）

[3]谢康和.复合地基固结理论研究现状与发展[J］.地基处理，1993，4（3）：1－14.XIE Kang－he.Current consolidation theories of composite foundation and its’development[J］.Ground Improvement，1993，4（3）：1－14.（In Chinese）

[4]卢萌盟，谢康和，王坤，等.考虑桩体内径向渗流的复合地基固结解[J］.固体力学学报，2009，30（2）：155－161.LU Meng－meng，XIE Kang－he，WANG Kun，etal.Analytical solutions for the consolidation of a compound foundation with consideration on the radial flow within the column[J］.Chinese Journal of Solid Mechanics，2009，30（2）：155－161.（In Chinese）

[5]朱百里，沈珠江.计算土力学[M］.上海：上海科学技术出版社，1990：100－121.

[6]徐洋.复合地基固结与变形的计算理论及数值分析[D］.杭州：浙江大学建筑工程学院，2004.XU Yang.Computational theory and numerical analysis for consolidation and deformation of composite foundation[D］.Hangzhou：College of Civil Engineering and Architecture，Zhejiang University，2004.（In Chinese）

[7]陈祖煜，周晓光，陈立宏，等.务坪水库软基筑坝基础处理技术[J］.中国水利水电科学研究院学报，2004，2（3）：167－172.CHEN Zu－yu，ZHOU Xiao－guang，CHEN Li－hong，etal.Foundation improvement techniques applied on a soft clay foundation of Wuping Dam[J］.Journal of China Institute of Water Resources and Hydropower Research，2004，2（3）：167－172.（In Chinese）

[8]邢皓枫，杨晓军，龚晓南.碎石桩复合地基试验及固结分析[J］.煤田地质与勘探，2005，33（3）：48－51.XING Hao－feng，YANG Xiao－jun，GONG Xiao－nan.Field tests and consolidation analysis of gravel pile composite foundation[J］.Coal Geology ＆ Exploration，2005，33（3）：48－51.（In Chinese）

[9]KIM Y T，PARK H II.Consolidation characteristics of SCP－reinforced composite ground[C］//Praceedings of Geo Congress 2006，New York：ASCE，2006.

[10］傅少君，王曼.振冲碎石桩地基有限元分析的复合模型研究[J］.岩土力学，2008，29（2）：375－380.FU Shao－jun，WANG Man.Study on composite model for vibro－replacement stone column foundation by FEM[J］.Rock and Soil Mechanics，2008，29（2）：375－380.（In Chinese）

[11］崔溦，张志耕，闫澍旺.碎石桩联合土工格栅复合地基处理湿地软基的机制研究[J］.岩土力学，2009，30（6）：1764－1768.CUI Wei，ZHANG Zhi－geng，YAN Shu－wang.Mechanism of composite ground with stone columns and geogrid in wet land[J］.Rock and Soil Mechanics，2009，30（6）：1764－1768.（In Chinese）

[12］谢康和.砂井地基固结理论、数值分析与优化设计[D］.杭州：浙江大学建筑工程学院，1987.XIE Kang－he.Sand drained ground：analytical ＆numerical solutions of consolidation and optimal design[D］.Hangzhou：College of Civil Engineeing and Architecture，Zhejiang University，1987.（In Chinese）

[13］谢康和，周健.岩土工程有限元分析理论与应用[M］.北京：科学出版社，2002：223－292.

[14］殷宗泽.土工原理[M］.北京：水利水电出版社，2007：346－350.