基于熵的混合粒子群算法在柔性调度中的应用＊

黄英杰，姚锡凡，古耀达

（1.华南理工大学 机械与汽车工程学院，广东 广州 510640；2.广州计量检测技术研究院，广东 广州 510030）

粒子群算法或粒子群优化（particle swarm opti mizer，PSO）算法是由Kennedy和Eberhart提出的源于群智能的一种智能优化算法[1］.它通过模拟鸟群的觅食行为来求解问题，初始产生一组随机解，每个个体在搜索空间以一定的速度飞行，并根据自己和同伴的飞行经验进行调整.PSO有着个体数目少、计算简单、鲁棒性好等优点，目前已广泛应用于函数优化、神经网络训练、模糊系统控制等应用领域.而信息熵（Information entropy）则是一个数学上颇为抽象的概念，不妨把信息熵理解成某种特定信息的出现概率（离散随机事件的出现概率）.一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高.信息熵可以说是系统有序化程度的一个度量.

柔性车间调度问题[2］（Flexible Job Shop Scheduling Problem，FJSP）是对经典Job Shop调度问题的扩展，它不仅是NP－Hard问题，而且与经典Job Shop问题相比，其可行解空间增大，问题的复杂性更高.尽管已经有很多算法用于求解这类调度问题，比如遗传算法、粒子群算法、禁忌搜索算法等优化算法，然而单独的一种算法求解的效果并不理想.为此，本文把粒子群算法、遗传算法和模拟退火算法结合起来，并根据种群熵来调节自适应惯性系数和变异概率，提出一种应用于柔性车间调度优化的基于熵的混合粒子群算法.

1 问题描述

柔性车间调度问题是对经典Job Shop调度问题的扩展，不但继承了Job Shop问题的所有特征，而且增加了新的求解难度.将柔性Job Shop调度问题描述为：将n个加工顺序不同的工件在m（m＞2）台机器上加工，其中，每道工序可以在多台机器上加工，每台机器也可以执行多种工序的加工任务.已知：工件集P＝ ｛p1，p2，…，pn｝，pi为第i个工件，i＝1，2，…，n；机器集M＝ ｛m1，m2，…，mn｝，mj为第j号机器，j＝1，2，…，m，机器集中存在加工能力相同、可以完成相同工序的机器称为并行机；工序 序 列 集OP＝ ｛op1，op2，…，opn｝，而opi＝｛opi1，opi2，…，opin｝ 为工件pi的工序序列.与经典Job Shop调度问题不同，柔性Job Shop调度问题中，工件的工序数量不一定等于机器数，即在车间内可能存在并行机或可以加工两种及以上工序的多功能机器；每个工件使用每台机器的时间矩阵T，tij∈T为第i个工件pi使用第j个机器的时间.tij＝0表示工件pi不使用机器j.此外柔性Job Shop调度问题还需满足以下条件：各工件在每台机器上使用的次数可以多于1次；各工件使用每台机器的顺序可以不同，即可以有opi≠opd（i≠d）；各工件具有相同的加工优先权；各工件加工过程中没有新工件加入，也不能临时中断加工.

2 用于柔性车间调度的粒子群算法

粒子群优化算法是一种由Kennedy和Eberhart于1995年提出的群智能进化算法.粒子群优化算法采用“群”和“进化”的概念，根据粒子的适应度值进行操作.每个粒子在n维搜索空间以一定速度飞行，且飞行速度由个体的飞行经验和群体的飞行经验共同进行动态调整.设种群的规模s，Xi＝（xi1，xi2，…，xin）为粒子i的当前位置；Vi＝ （vi1，vi2，…，vin）为粒子i的当前速度；Pi＝（pi1，pi2，…，pin）为粒子i的历史最好位置，称为个体最好位置.对于最小化问题，历史最好位置就是指适应度函数值最小的位置，群体中所有粒子经历过的最好位置为Pg（t），称为全局最好位置，则基本粒子群优化算法的进化方程可以描述为：

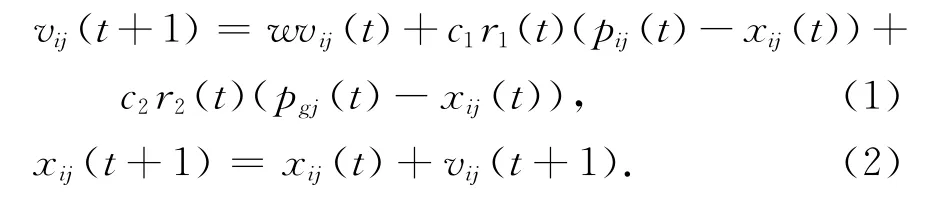
式中：vij（t），xij（t），vij（t＋1），xij（t＋1）分别为第i个粒子在第t代和第t＋1代的飞行速度和位置；下标j为粒子的第j维；下标i为粒子i；t为第t代；w为惯性系数；c1和c2分别为个体粒子的加速常数和群体粒子的加速常数，通常取值0～2；r1，r2分别为（0，1）内的随机数.从式（1）的速度更新公式可以看出，c1为调整粒子在历史最优方向上的步长，c2为调整粒子在全局最优粒子方向上的步长.为了减少在进化过程中，粒子离开搜索空间的可能性，vij通常限定在 [－vmax，vmax］内，如果问题的搜索空间限定在 [－xmax，xmax］内，可以设定vmax＝k×xmax，0.1＜k＜1.0.

2.1 粒子的编码和解码

在求解柔性单车间调度优化问题的粒子群算法中，每个粒子对应一种调度方案.根据柔性车间调度的问题，这里用一个2L（L＝∑n j＝1nj为总工序数）维的向量来表示粒子的位置向量.实际上，这个位置向量由两个L维的向量组成，即工序向量Xprocess[L］和机器向量Xmachine[L］，工序向量Xprocess[L］由L个非零且不大于n（工件数）的自然数组成，自然数的顺序决定了工件工序的加工顺序.在这里，借鉴遗传算法中的基于操作的编码方法，即每个工序向量用L个代表操作的位组成，是所有操作的一个排列.比如工序向量Xprocess[L］为[2 1 1 2 2 3 1 3 3］，其中的1表示工件1，2表示工件2，3表示工件3，第1次出现的1代表工件1的第1道工序，第2次出现的1代表工件1的第2道工序，第3次出现的1代表工件1的第3道工序，工件2和工件3的含义也由此类推.机器向量Xmachine[L］由L个非零且不大于m（机器数）的自然数组成，代表加工Xprocess[L］对应位置工序的机器号.

2.2 位置向量和速度向量的计算

粒子群算法是一种属于连续空间的优化算法，而柔性作业车间调度问题是离散的非数值优化问题，因此在迭代计算过程中做如下修改：

1）对于Xmachine[L］，由于机器向量的取值为[1，m］的整数，如果按照公式（2）计算出来的是小数，则采取向下取整的办法进行修正，如果按照公式（2）计算出的结果超出取值区间，则按照边界取值.

2）对于Xprocess[L］，由于柔性车间调度优化问题为工序顺序的排序问题，因此采用迭代运算.假设初始值为.

维数： 1 2 3 4 5 6 7 8 9.

Xprocess[L］：1 1 1 2 2 2 3 3 3（初始值）.经过某次迭代运算得到如下结果：

Xprocess[L］（按照公式（2）计算后的值）.

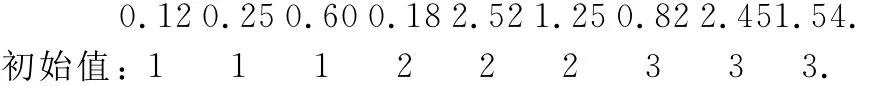
将计算后的数值按照由小到大进行排序，将与计算后的值所对应的初始值进行重新排列，得到如下结果.

这次迭代过后的结果为[1 2 1 1 3 2 3 3 2］，经过这样转化就可以得到一个满足要求的可行解.

2.3 基于熵的混合粒子群算法

2.3.1 模拟退火算法

模拟退火算法[3］来源于固体退火原理，将固体加温至充分高，再让其逐渐冷却，加温时，固体内部粒子随温度升高变为无序状，内能增大，而徐徐冷却时粒子渐趋有序，在每个温度都达到平衡态，最后在常温时达到基态，内能减为最小.根据Metropolis准则，粒子在温度T时趋于平衡的概率为e－ΔE/（λT），其中E为温度T时的内能，ΔE为其改变量，λ为Boltzmann常数.用固体退火模拟组合优化问题，将内能E模拟为目标函数值f，温度T演化成控制参数t，即得到解组合优化问题的模拟退火算法：由初始解i和控制参数初值t开始，对当前解重复“产生新解→计算目标函数差→接受或舍弃”的迭代，并逐步衰减t值，算法终止时的当前解即为所得近似最优解，这是基于蒙特卡罗迭代求解法的一种启发式随机搜索过程.退火过程由冷却进度表（Cooling Schedule）控制，包括控制参数的初值t及其衰减因子Δt，每个t值时的迭代次数L和停止条件S.2.3.2 混合粒子群算法

由于粒子群算法特有的粒子间单向信息流的影响，粒子群算法具有非常快的收敛速度，经过不太多次的迭代进化后，种群中的各粒子往往具有相同的特征.这样，导致种群缺乏多样性，难以跳出局部最优，往往很容易形成过早收敛.然而，模拟退火算法是在某一初温下从某一起点开始邻域搜索，伴随温度参数的不断下降，结合概率性地突跳特性在解空间中随机寻找目标函数的全局最优解，即在局部最优解能概率性地跳出并最终收敛于全局最优解[4］，但其计算时间长，效率低，因此把粒子群算法和模拟退火算法相结合能更好地解决优化问题.

选择粒子群算法与模拟退火算法结合，主要有以下几方面的原因：首先是优化机制的融合，SA通过赋予搜索过程一种随时变化且最终趋于零的概率突跳性，从而可有效的避免陷入局部最小并最终趋于全局最优；PSO则通过全局最优粒子和个体最优粒子的飞行信息指导来实现优化，对选择机制上如此差异的两种算法进行混合，有利于丰富优化过程的搜索行为，增强全局和局部意义下的搜索能力和效率.其次是优化操作的结合，SA算法在每一时刻仅保留一个解，缺乏冗余和历史搜索信息，而PSO的速度更新过程中继承了种群中全局最优个体和历史个体最优粒子的部分信息，使得粒子始终保持向好的方向进化.把这些作用不同的优化操作相结合，丰富了优化过程中邻域搜索结构，增强了全局空间的搜索能力.再次是优化行为的互补，若粒子群算法收敛准则设计不好，PSO经常会出现进化缓慢或“早熟”收敛的现象；而算法SA的优化行为对退温历程具有很强的依赖性，而理论上的全局收敛对退温历程的限制条件很苛刻，因而SA优化时间性能较差.若将两种算法相结合，则SA的两准则可控制算法收敛性以避免出现“早熟”收敛现象，并行化的抽样过程可提高算法的优化时间性能.

PSOSA混合算法在优化机制、结构和操作上结合了PSO和SA的特点，充分发挥了粒子群算法良好的搜索能力和模拟退火算法有效避免陷入局部最优并最终趋于全局最优的特性，使PSO和SA互相取长补短，提高算法寻优性能.

2.4 熵的引入

信息熵是信息论中用于度量信息量的一个概念.一个系统越是有序，信息熵就越低；反之，一个系统越是混乱，信息熵就越高[5－6］.所以，信息熵也可以说是系统有序化程度的一个度量.在此，我们把种群看作是一个系统，用种群中个体基因的信息熵来衡量种群中个体的差异程度，而粒子群算法的w取值就受种群信息熵的控制.在粒子群算法中，当w取值范围较大时，有利于对解空间进行大范围搜索，但这种情况下由于搜索过于粗略往往使得搜索的精度不高；而当w取值范围较小时，会改善搜索精度，但算法却可能陷入局部极值.因此，本文采用公式（3）对w进行自适应变换，使其在搜索过程中逐步减小.在迭代搜索的开始阶段，w足够大使得算法在较大搜索空间里具有更好的全局搜索能力；随着迭代次数的增加，w的值自适应地减小，以提高算法搜索到最优解的精度.变异概率Pm用公式（4）进行自适应变换，当种群中个体差异程度较低时，表示种群中的个体趋于一致，Pm自动地变大以增加种群的多样性，摆脱局部最优，而当种群中个体的差异程度较高时，表示种群中个体较分散，Pm自动地减小以保护优良个体的生存.

因此采用如下的方式调节惯性参数w：假设种群中有M个个体，每个个体由2n个基因组成，设Rj是M个个体第j位基因值的集合，bij表示第i个个体第j位基因值在Rj中的重复个数，Pij表示第i个个体第j位基因值在Rj中的占有率，那么种群中个体第j位基因的信息熵就可用下式计算[7］：

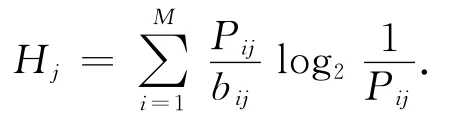
种群的多样性就可用种群中所有个体n个基因位的平均信息熵H来表示[7］：

式中：w1为允许的最大惯性系数；w2为允许的最小惯性系数；Pm1为允许的最大变异概率；Pm2为允许的最小变异概率.

2.5 基于熵的混合粒子群算法（HPSO）

利用粒子群算法和模拟退火算法相结合来求解柔性车间调度问题，其采用步骤为：

1）设定粒子群算法的惯性系数、加速常数、种群数和模拟退火算法的退火速率、初始温度和终止温度，随机初始化位置向量和速度向量.

2）对于每个粒子，用公式（1）计算速度向量Vprocess[L］和Vmachine[L］，用公式（2）计算位置向量Xprocess[L］和Xmachine[L］，并根据种群熵计算公式计算该代种群的种群熵.

3）对各粒子进行解码，计算各个粒子的适应度函数值（加工完成时间的倒数），寻找各粒子的最优解Pi和全种群的最优解Pg.

4）对于某个粒子，如果其适应度值优于历史最优位置的适应度值，则记当前的适应度为该粒子的最优适应度，当前的位置为该粒子的历史最优位置.

5）寻找本代种群的最优解，判断其是否优于全种群的最优解Pg，如果优于全种群的最优解，则用本代种群的最优解更新全种群的最优解.

6）判断Metropolis准则是否满足，如果是，则分别对最优解Pg的位置向量Xprocess[L］和Xmachine[L］进行模拟退火操作T（t＋1）＝λT（t），并存储当前的最优状态，转9），如果否，则转7）.

7）由当前的稳定状态产生新状态，并以概率min[1，exp（－Δt＇/T）］接受新状态，并返回6）.

8）根据步骤2）中计算出的种群熵，用公式（3）更新惯性系数w，用公式（4）更新变异参数Pm，同时对各个个体最优粒子Pi以Pm的概率进行变异操作.

9）判断迭代次数是否大于规定值，如果小于，则转步骤2）.

10）优化结束，输出最优解.

3 实例分析

以F46（4×6），F88（8×8），F1010（10×10），MK07（20×5）问题的数据为例，进行连续10次的优化计算，其中种群数为100，进化代数为50，ωmax＝1.2，ωmin＝0.2，c1＝c2＝2.0，λ＝0.9，变异概率Pm1＝0.4，Pm2＝0.05，连续10次运行的结果如表1所示.由仿真结果可以看出，用本文提出的混合粒子群算法每次都能求出最优解，其优化效果明显优于标准粒子群算法，但优化时间大于标准粒子群算法的优化时间.图1为F1010问题优化时的PSO算法、混合PSO算法收敛曲线图.

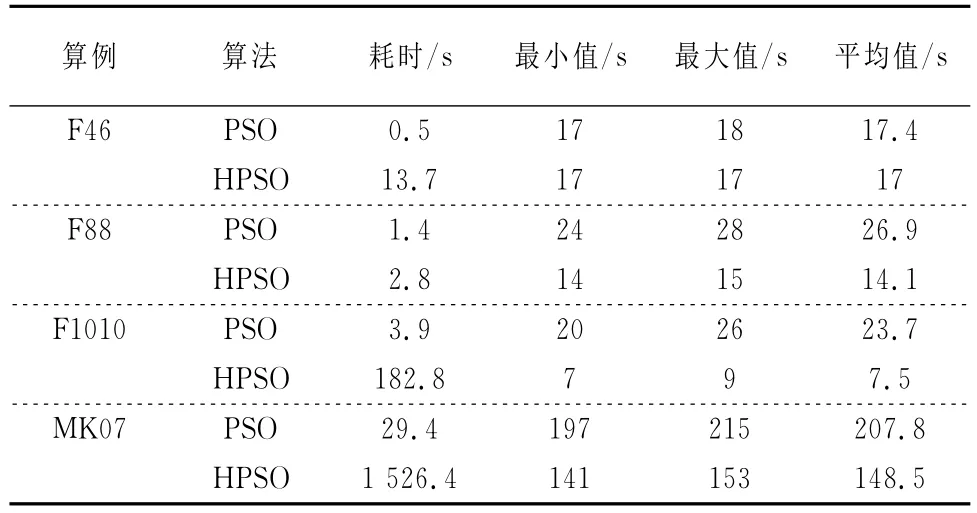
表1 算例的优化结果Tab.1 Optimization results for the examples

图1 PSO和混合PSO算法收敛曲线图Fig.1 Convergence curves of PSO and hybrid PSO

4 结 论

本文针对较大规模的柔性车间调度问题，将粒子群算法、遗传算法、模拟退火算法和种群熵相结合，提出一种应用柔性车间调度优化的混合粒子群算法.实例仿真结果表明，该算法能很好地求解各种规模的柔性车间调度问题，与传统的优化算法相比，在优化精度上具有明显的优越性.该算法对柔性车间调度优化的研究进行了有益的探索，为混合智能优化算法在调度问题中的应用提供了有益的借鉴.

[1]KENNEDY J，EBERHART R C.Particle swarm optimization[C］//Proceedings IEEE International Conference on Neural Networks，IV.Piscataway，NJ：IEEE Service Center，1995：1942－1948.

[2]谷峰，陈华平，卢冰原，等.粒子群算法在柔性工作车间调度中的应用[J］.系统工程，2005，23（9）：20－23.GU Feng，CHEN Hua－ping，LU Bing－yuan，etal.Particle swarm optimization for flexible job shop scheduling[J］.Systems Engineering，2005，23（9）：20－23.（In Chinese）

[3]顾元宪，项宝卫，赵国忠.一种改进的连续变量全局优化模拟退火算法[J］.系统工程理论与实践，2005，4：103－109.GU Yuan－xian，XIANG Bao－wei，ZHAO Guo－zhong.An improved simulated annealing algorithm for global optimization problems with continuous variables[J］.Systems Engineering Theory ＆Practice，2005，4：103－109.（In Chinese）

[4]刘鑫朝，颜宏文.一种改进的粒子群优化RBF网络学习算法[J］.计算机技术与发展，2006，16（2）：185－187.LIU Xin－chao，YAN Hong－wen.A RBF neural network learning algorithm based on improved PSO[J］.Computer Technology and Development，2006，16（2）：185－187.（In Chinese）

[5]PIPLANI R，WETJENS D.Evaluation of entropy－based dispatching in flexible manufacturing system[J］.European Journal of Operational Research，2007，176（1）：317－331.

[6]SARDIS G N.Entropy in control engineering[M］.Singapore：Word Scientific Publ Co Pte Ltd，2001.

[7]刘林.一类离散制造业生产过程中的优化问题研究[D］.合肥：合肥工业大学管理学院，2009.LIU Lin.Research on optimization problem of manufacturing process in a discrete manufacturing industry[D］.Hefei：College of Management，Hefei University of Technology，2009.（In Chinese）