RLS算法及其改进形式在信号分离中的应用分析

邵亚勇，竺小松

（解放军电子工程学院，安徽 合肥 230037）

0 引言

自适应滤波算法，作为信号处理的一个重要分支广泛应用于智能控制、信道估计、信道均衡、噪声对消、回声对消等各种领域。通常自适应滤波算法采用RLS或LMS(最小均方)算法，RLS算法与LMS算法相比，具有收敛速度快、稳态性能好等优点，但是其又在一定程度上增加了算法的复杂性。同时RLS算法存在固定遗忘因子λ造成的收敛速度与稳态误差之间的矛盾，在实际应用中根据需要对RLS出现了多种改进形式，但归纳起来，主要是从两个方面着手：其一采用可变遗忘因子的方法，如文献[1-4]所提出的方法，文献[1]通过最小均方梯度的动态变化来控制遗忘因子的变化，文献[2]采用恢复误差信号中的系统噪声来实现对可变遗忘因子的控制，文献[3]对遗忘因子的控制通过对输入信号自相关矩阵的逆矩阵的梯度来实现，文献[4]设定遗忘因子λ值的大小由误差决定,通过找一个临界误差点，当小于这个值时，λ由一条曲线趋近于1,当大于这个值时，λ由一条曲线趋近于λmin；其二对RLS算法改进从对信号的协方差矩阵的逆矩阵从发，给逆协方差矩阵加一自扰动项，当输入信号或信道突变的情况下，能够及时进行跟踪上信道的变化。这种方法主要有D.J.Park和B.E.Jun提出的具有快速跟踪能力的自扰动RLS算法(SRLS)[5]， Kwang-Seop Eom等提出的基于卡尔曼滤波具有快速跟踪和抗噪声的RLS算法(ISPRLS)[6]。当前除从这两个角度改进之外，还出现了对RLS算法中的增益向量进行调整以提高系统的收敛速度的RLS算法[7]。以上所提到的这些改进方法，多是应用于噪声对消、信道均衡与信道估计，我们现将这些方法应该于混叠信号分离，通过仿真比较各种方法在信号分离中的优劣。

1 RLS自适应滤波器的原理[8]及在信号分离中的应用模型

将最小二乘方法推广为自适应的方法，其目的就是通过递推的方法来简化运算。在代价函数中引入指数加权因子后可以表达为：

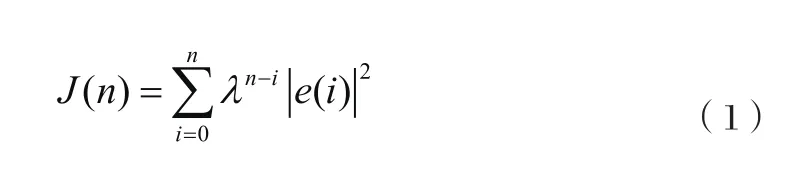
上式中λ为遗忘因子，取值范围是0<λ<1，它的作用是对离n时刻越近的误差加比较大权重，而对离n时刻越远的误差加比较小的权重[9]。其中e(i)是期望响应d(i)与i时刻的抽头输入经横向滤波器加权之差。即为：

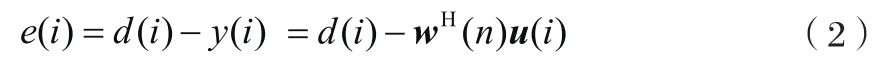
经过推导，可以将RLS算法归纳如下：

初始化：w( 0) = 0 ，P( 0)=δ-1I，其中δ为正则化参数。对于每一时刻，n= 1 ，2，...计算：

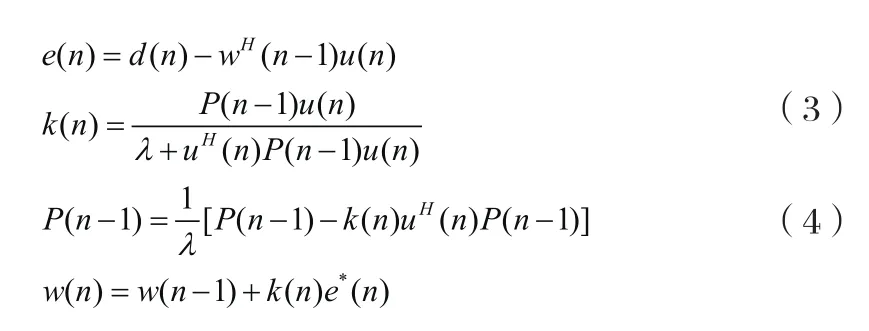
为了将RLS算法应用于信号分离之中，我们不妨假设混合信号为s(n)，其含有信号x(n)和y(n)。

首先通过信号检测得到信号特征比较鲜明的信号x(n)的相关特征参数，对其进行信号重构，恢复出信号x(n),然后将恢复出来的信号输入到自适应滤波器，经过横向滤波器加权系数的调整得：

用此信号与混合信号s(n)进行对消，将对消后的信号分成两路，一路作为误差信号输入到自适应滤波器控制器，对横向滤波器的加权系数进行控制，另一路作为混合信号中y(n)的估计信号yˆ(n)，即为分离信号所得的输出值。图1为信号分离的基本原理图。

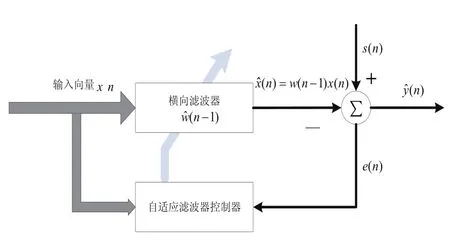
图1 自适应信号分离模型图

2 RLS算法的常见改进形式

在RLS算法的众多改进形式中，我们选择其中比较成熟而且运算量较为优化的改进方法来说明。对于可变遗忘因子，李倩茹提出的VFF-RLS算法具有运算简单，原理清晰的特点，该方法对λ的修正函数为：

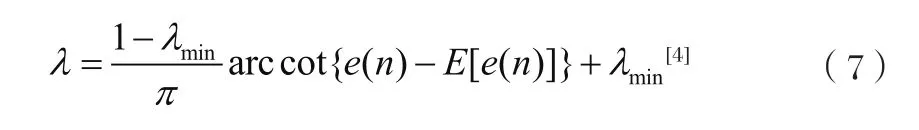
在上式中根据n时刻误差信号的大小对遗忘因子进行调整，选择误差均值E[e(n)]作为一个临界值，当n时刻的误差信号大于此值时，λ趋近于最小值λmin；否则λ趋近于1。这样可以保证误差在E[e(n)]附近摆动，进行缓慢变化，以缓冲λ变化过快带来的跟踪效果差的问题。

对输入信号自相关矩阵的逆矩阵P(n)进行调整的方法中，主要是采取加上一个与误差有关的自扰动项，在信号或信道发生突变时，避免k(n)趋于0而失去跟踪性能。SRLS算法[5]加入的自扰动项为：

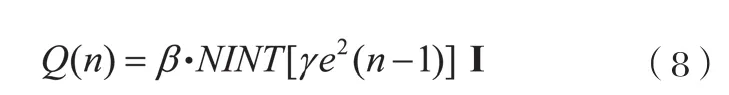
I为单位矩阵，β、γ均为常数，该算法具有快速跟踪的能力，但对噪声比较敏感。之后Kwang-Seop Eom提出的ISPRLS算法对其进行了改进，根据卡尔曼滤波实现对信号遗忘因子的控制，不需要根据信噪比的条件来调整滤波器参数。ISPRLS算法[6]的P(n)项为：

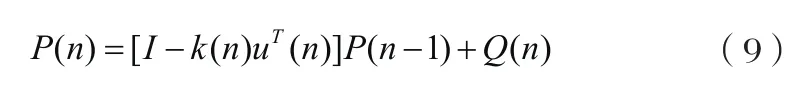
其中自扰动项Q(n)为：

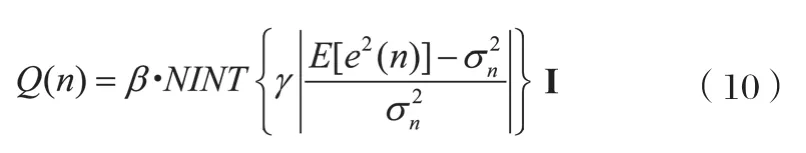
式（10）中，I为单位矩阵，NINT为取整函数，β、γ均为常数。

由于增益向量在RLS算法中发挥着重要的作用，所以对增益向量的适当调整也可以有效地促进算法的收敛速率，由Anum Ali等提出的基于增益向量来促进收敛速度的RLS方法[7]的改进形式如下：

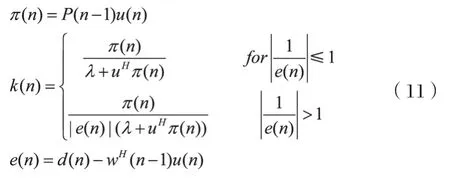
我们不妨将这种方法称为GV-RLS算法，GV-RLS算法的改进并没有对自适应运算的复杂性造成过多的影响，计算步骤较为简单，只需要预先判断误差信号倒数的绝对值是否大于1即可。

3 RLS算法及其改进形式在信号分离中的性能分析

自适应算法的选择取决于一个或多个因素，主要判断标准有：收敛速度、失调、跟踪性能、鲁棒性、计算要求、结构、数值特性等因素[8]。无论对RLS算法的改进从哪个方面出发，都要在满足收敛速率和稳定性的同时，尽可能地减小运算量。而将自适应算法应用于信号分离中去，在考虑之前的判断标准的同时，需着重考虑经系统分离出的信号失真情况，如果误差较大，很难准确地从系统中分离出所期望的信号。我们以RLS算法、VFFRLS算法和GV-RLS方法为例，检验它们在大信号和小信号混合的情况下，将小信号分离出来的效果；其次使用这些方法，完成信号与噪声的分离，检测对噪声的消除效果。通过以上两个步骤，可以实现在一个含有噪声和大信号干扰的复杂电磁环境中，有效检测出小信号的目的。

混叠信号为s=x+y；我们力求在大信号x的背景下，检测出小信号y。首先两信号的时域波形图和混叠信号的时域波形图分别如图2所示。

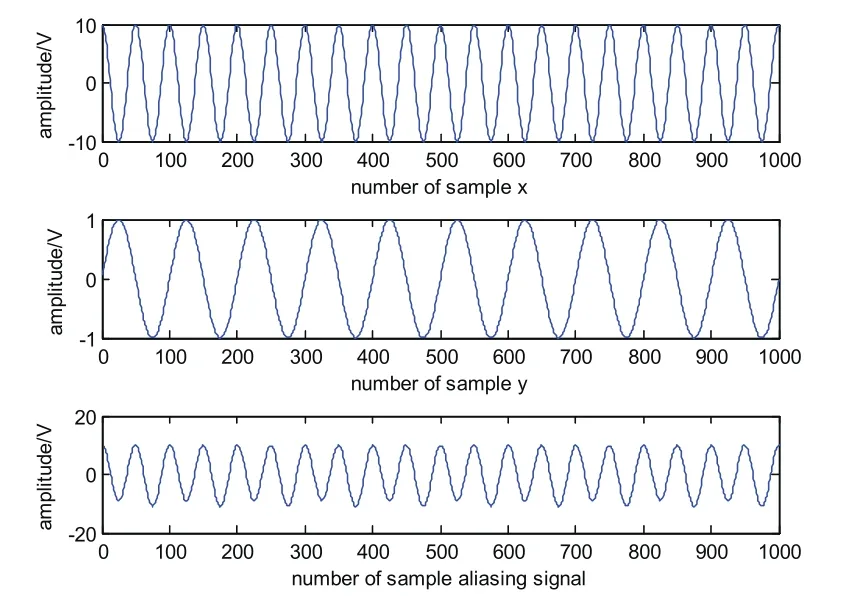
图2 原始信号时域波形图

假设RLS、GV-RLS方法采取相同的遗忘因子λ=0.98，VFF-RLS算法的最小遗忘因子λmin也取为0.98，经过仿真发现使用这3种方法，都能较好地完成大小信号的分离，实现强信号背景中检测出弱信号的目的。经过估计输出的大小信号时域波形图如图3所示。

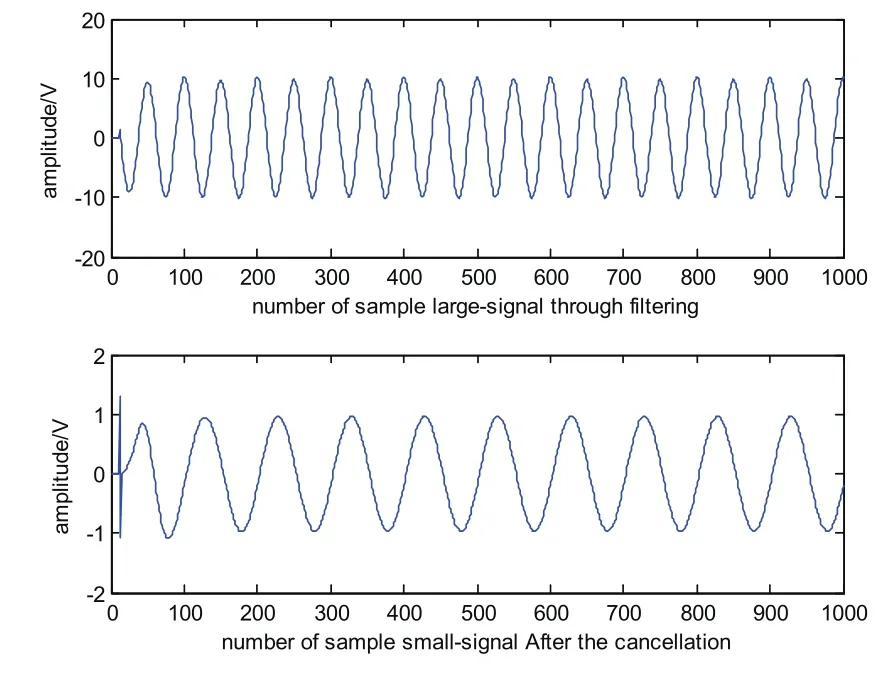
图3 经自适应滤波后的大、小信号波形图

为了进一步说明3种方法在信号检测中的收敛速度及误差情况，我们以检测估计出的小信号与原始小信号的误差的平方进行比较，如图4所示。从3种方法检测出的小信号与原始小信号的误差平方图可以得出，3种方法在进行两个正弦信号分离时的收敛速度基本相当，但在收敛之后，RLS、GV-RLS还会伴随一些有规律的干扰信号影响，但是VFF-RLS实现了很好的收敛性能，只有极小的误差出现。因此在进行比较精确的信号分离时，我们可以首选VFF-RLS的方法。

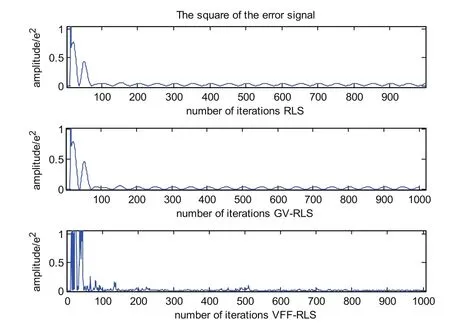
图4 3种方法检测出的信号与原始小信号的误差平方图

为了在噪声环境下检测出所需要的有用信号，我们将混叠有噪声的信号输入到自适应滤波器中，同样采取这3种方法进行对消。假定所选的混叠信号信噪比为0，滤波器的阶数为12，遗忘因子为λ=0.97， VFF-RLS最小遗忘因子为λmin=0.97。首先仿真得到噪声、信号和受到噪声干扰的信号时域波形如图5所示。

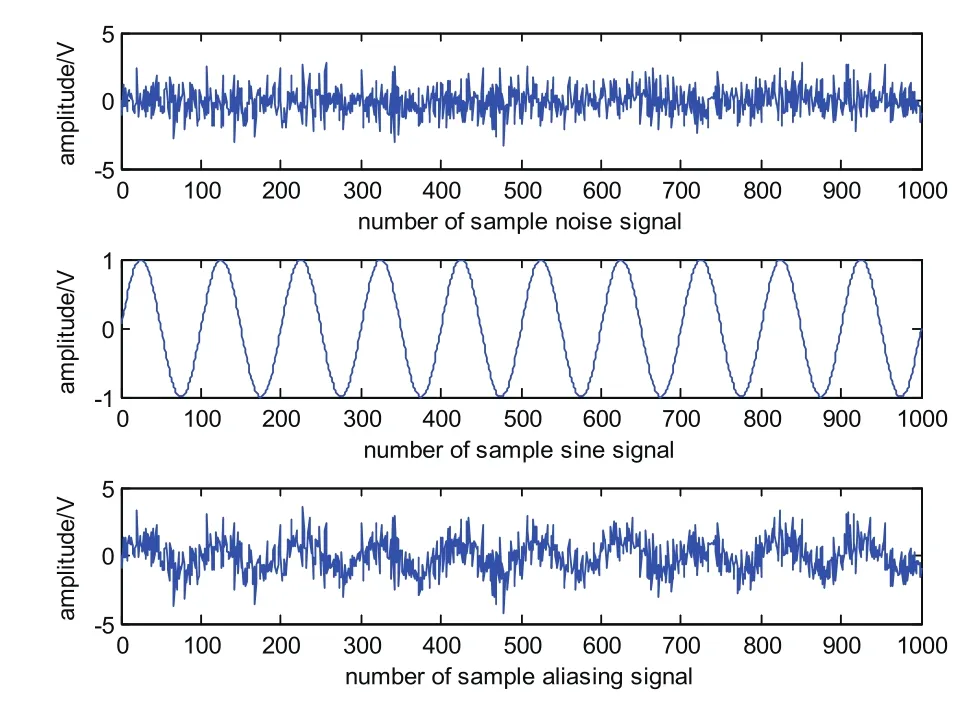
图5 信号与噪声的时域波形图

将估计的噪声信号输入到自适应滤波器的输入端，以混叠信号为期望信号，分别应用3种方法，得到的正弦信号时域图为如图6所示。 从图6可以看出，通过VFF-RLS滤波得到的正弦信号与其他两种方法相比，具有更小的失真，能较好地恢复出受噪声污染的正弦信号。同样比较估计信号与原始信号的误差平方来检验收敛速度和误差状况，如图7所示。

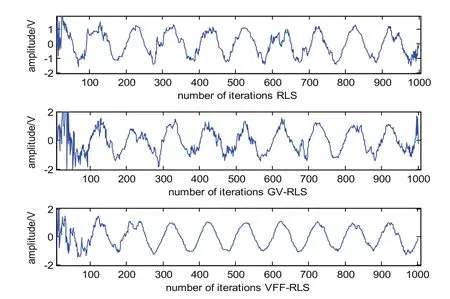
图6 3种方法滤波后正弦信号波形图

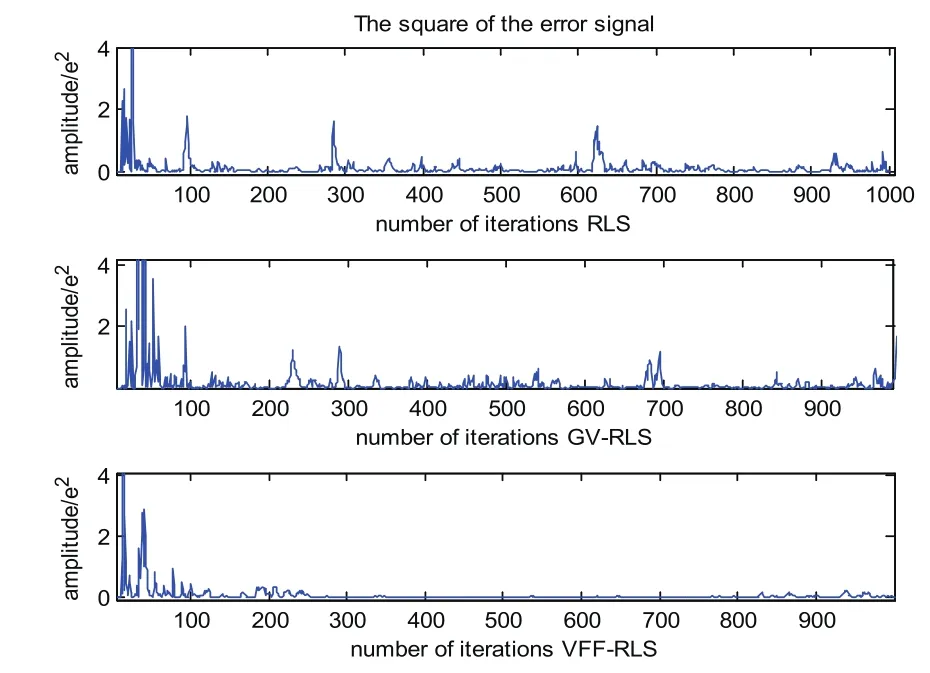
图7 3种方法去噪后的信号与原始信号的误差平方图

比较图6、图7可以发现，在相同条件下，3种方法都能在比较小的失真情况下将正弦信号从噪声中分离出来，但是VFF-RLS算法与RLS、GV-RLS算法相比，能够获得更好的信号效果；同时通过信号误差的平方比较，可以发现GV-RLS算法与RLS、VFF-RLS算法相比，收敛速度较慢，VFF-RLS在信号趋于平稳后，抗杂波和干扰的能力更强。

4 结论

本文在分析RLS算法及其几种常见改进形式的基础之上，将他们从传统的噪声对消、信道均衡、信道估计的应用转移到对混叠信号的分离中去，实现在复杂的噪声背景和大信号的干扰下，准确检测出小信号的目的。通过在仿真中对原有方法的调整，比较他们在两个不同信号之间的信号分离及信号和噪声混叠情况下的信号分离效果。经过验证，VFF-RLS在这些方法中，无论是收敛速度还是分离得到的信号效果都优于其他方法。

[1]C.F.So, S.C.Ng,S.H,Leungc.Gradient based variable forgetting factor RLS algorithm[J].Signal Processing,2003,83:1163-1175.

[2]Constantin Paleologu, Jacob Benesty,Silviu Ciochina.A Robust Variable Forgetting Factor Recursive Least-Squares Algorithm for System Identification[J].IEEE Signal Processing Letters,2008,15:597-600.

[3]Hadi Sadoghi Yazdi, Mehri Sadoghi Yazdi,Mohammad Reza Mohammadi.A Novel Forgetting Factor Recursive Least Square Algorithm Applied to the Human Motion Analysis[J].World Academy of Science, Engineering and Technology,2009,57:969-976.

[4]李倩茹,王于丁,张晓芳.一种变遗忘因子RLS算法的分析与仿真[J].现代电子技术,2008,17:45-47.

[5]D.J.Park,B.E.Jun.Selfperturbing Recursive Least Squares Algorithm with Fast Tracking Capability[J].Electronic Letters.1992,28:558-559.

[6]Kwang-Seop Eom, Byung-Eul Jun,Dong-Jo Park.Fast tracking and noise-immunised RLS algorithm based on Kalman filter[J].Electronic Letters.1996,3211-2312.

[7]Anum Ali,Anis-ur-Rehman,Rana Liaqat Ali.An Improved Gain Vector to Enhance Convergence Characteristics of Recursive Least Squares Algorithm[J].International Journal of Hybrid Information Technology.2011,4:99-107.

[8]西蒙·赫金.自适应滤波器原理[M].4版.北京:电子工业出版社,2010.

[9]张贤达.现代信号处理[M].北京:清华大学出版社,2002.