保障使命任务分解与流程集成方法研究＊

冯浩源 吕卫民 江式伟

（1.海军航空工程学院研究生管理大队 烟台 264001）（2.海军航空工程学院飞行器工程系 烟台 264001）

1 引言

在保障使命分解方法研究方面，目前的分解方法包括：按区域分解法、按目标分解法、按功能分解法、按活动类型分解法等［1］。这些方法可以将使命分解到具体的子任务或者原任务程度，如图1所示。

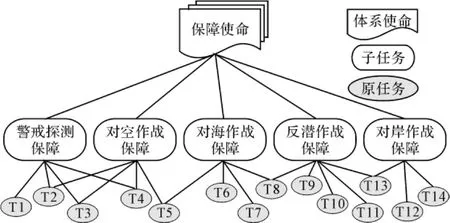
图1 使命任务分解示意图

根据此图可以很直观的看出使命构成，从而为军事保障需求分析奠定基础。但是这些方法均不能动态反映构成使命的子任务间的关系，分解的子任务为静态孤立的任务模型，不能满足对军事保障需求动态分析的要求，对保障能力进行评估时存在评价指标难以客观综合的突出问题。

在流程集成方法研究方面，目前大都采用排序论等方法，虽然可以求得确定条件下技术准备工作中辅助装备的最佳数量配置，以保证技术准备任务的按时完成和辅助装备的较高利用率［2］。但由于实践过程中，环境条件、保障设备条件以及保障人员状态都是随着时间发生变化的，因此必须将静态的流程转化为动态的流程集成模型，根据实际条件实时的给出最优流程，保证保障任务的顺利、高效完成。

保障流程这样的离散事件系统所表现出来的复杂性是很难通过采用某种单一的传统技术来完全体现的，而Petri网则以其特有的处理离散事件系统的能力而备受关注，因其既可较好的体现系统的静态结构，又可通过托肯的触发运行来表现系统的动态特征，再加上丰富的数学理论支持及众多的分析技术，使之成为离散事件系统优秀的建模、分析和仿真工具［3］。

因此，本文提出了一种基于保障模式组合的保障使命分解方法，并选取DoDAF产品中的OV－5视图，对任务进行分解，以得到具体活动集合。在得到活动集合并完成资源集成的基础上，通过构建基于Petri网的流程动态规划模型，以完成实时优化保障任务流程的目标。

2 保障使命任务分解与建模

2.1 保障使命分解

由于保障的最终目标是完成对作战使命任务的支持，因此对于保障体系使命的分解，可以参考作战使命分解为作战模式的方法，将保障使命分解为数种保障模式，保障模式通过组合的方式完成对作战模式的支撑。

同时考虑到实际的保障工作通常是一项保障任务围绕一种主战装备开展的工作模式，可以将保障模式直接分解到对应各类型主战装备保障任务的层次上。可见，对于特定的作战任务，根据作战模式可以得到参战主战装备的数量与类型，据此可以得到此时为完成使命的保障模式组合，即保障任务的组合，如图2所示。

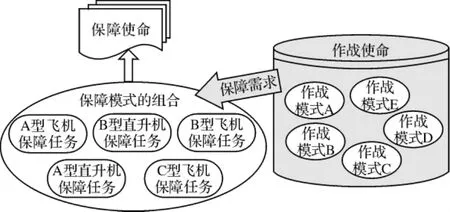
图2 保障体系使命分解图

2.2 保障任务静态建模

将保障使命分解到任务层次后，对保障任务进行静态建模。根据任务的形式化描述方法，对保障任务的形式化描述需要四方面信息：目标描述、装备描述、活动描述以及活动间关系描述。为对其进行形式化的描述，现对如下内容进行定义：

定义1（保障任务）对于任何一个保障任务，其都可被形式化描述为一个四元组

其中，TO＝｛TO1，TO2，…，TOn｝表示保障任务的目标集合；TE＝｛TE1，TE2，…，TEn｝表示保障任务的装备集合；TA＝｛TA1，TA2，…，TAn｝表示保障任务的活动集合；TR＝〈SeqR，CndR，AndR，OrR，ConcR，SynR，CycR〉表示作战任务的活动间关系集合。

定义2（保障任务的目标）保障任务的目标指保障任务的完成条件或目标，对于不同的目标，用TOi（i＝1，2，…，n）表示。

定义3（保障任务的装备）保障任务的装备是指参与完成保障任务活动的各类装备所构成的集合，用（i＝1，2，…，n）表示。

定义4（保障任务的活动）保障任务的活动是保障任务的基本元素，具有不可分割性和特定目标性。它是指在满足一定的条件下，可由一定的保障系统根据相关的规则、条例、条令完成过程动作。保障任务的活动可以用TAi（i＝1，2，…，n）表示。

定义5（保障任务活动间的关系）保障任务活动间的关系是指保障任务活动之间的相互约束和逻辑关系，即顺序关系（SeqR）、条件关系（CndR）、与关系（AndR）、或关系（OrR）、并发关系（ConcR）、同步关系（SynR）、循环关系（CycR）。

美国国防部体系结构框架DoDAF为体系结构的描述、表示及作战行动和业务运作过程的集成定义了一种通用的途径［4］。DoDAF由20多个产品构成，这些产品分别从作战视图、系统视图和技术视图对体系结构进行描述，根据任务描述需求在DoDAF框架中选取适当产品。

为描述任务目标和任务活动，选取OV－5任务活动图，OV－5能够实现对任务目标的集合TO＝｛TO1，TO2，…，TOn｝以及任务活动的集合TA＝｛TA1，TA2，…，TAn｝的描述；为描述任务装备，选取OV－2任务节点图、OV－4组织关系图以及OV－3任务信息交互矩阵，通过以上三个视图，可表现保障装备的集合TE＝｛TE1，TE2，…，TEn｝及集合内元素间的信息交换；为描述任务活动间关系，选取OV－6c任务事件跟踪描述图，OV－6c图涵盖了与活动间关系TR＝〈SeqR，CndR，AndR，OrR，ConcR，SynR，CycR〉相关的信息。

选取OV－5用于构建任务静态模型。对美军航母航空保障的典型任务进行分析并对任务的活动进行形式化描述后，可建立该任务的OV－5活动树状图，如图3所示。

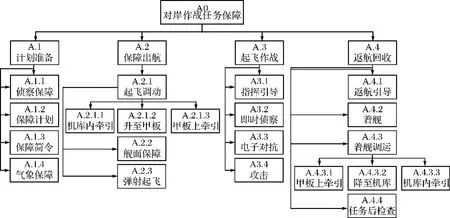
图3 OV－5任务活动树状图

2.3 保障任务分解

1）任务分解原则

（1）原则一，目标原则

以原任务关联到具体目标为依据，当具体目标的执行被分解到某一任务时，该任务可以优先确定为原任务。

（2）原则二，任务空间维度原则

从任务执行空间的维度进行进一步的分解，以全面考虑任务执行可能的情况。

（3）原则三，阶段划分原则

阶段划分是对任务执行过程与序列行动的考虑，在任务分解过程中从任务执行或实现的阶段划分来考虑是否需要进一步分解得到原任务。

（4）原则四，任务区域或方向原则

任务区域或方向原则是对保障主体进行以执行任务过程可能的路径选择、行进方向选择和任务区域选择的考虑。

根据美军航母航空保障使命特征，主要依据阶段划分的原则进行任务分解，在任务的分解过程中综合考虑原则一、原则三和原则四。

2）分解过程

定义1保障任务两个外部节点，分别为下达保障指令，以及确定保障任务结束。

定义2保障任务的输入为保障模式和保障规模，它们来源于外部节点，输出为任务结束，去向另一个外部节点。根据定义1、2美航母航典型对岸作战保障任务的前后关系图如图4所示。

图4 OV－5任务前后关系图

对岸作战保障这一任务进行分解，其下包含四个子任务，分别为：计划准备、保障出航、起飞作战和返航回收，如图5所示。

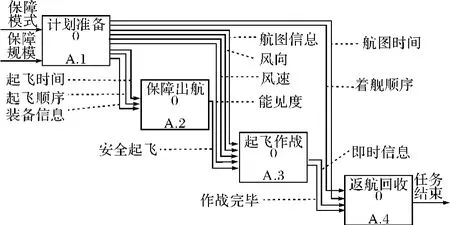
图5 对岸作战保障任务的分解视图

在这里可以根据需要选取继续对这四个子任务继续分解，如图6～9所示。

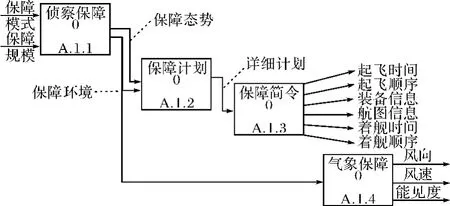
图6 计划准备准备子任务分解视图

3 基于Petri网的保障流程集成模型

通过前面使命任务分解与建模的工作，得到了具体的保障活动集合，为了优化组织活动以便高效地完成任务，需要完成资源集成、业务流程规划与资源配置。为此，本文提出了一种基于Petri网的流程集成模型。

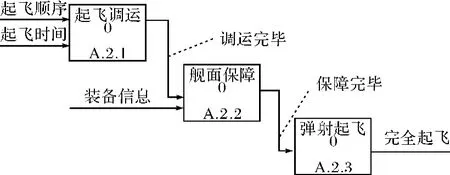
图7 保障出航子任务分解视图

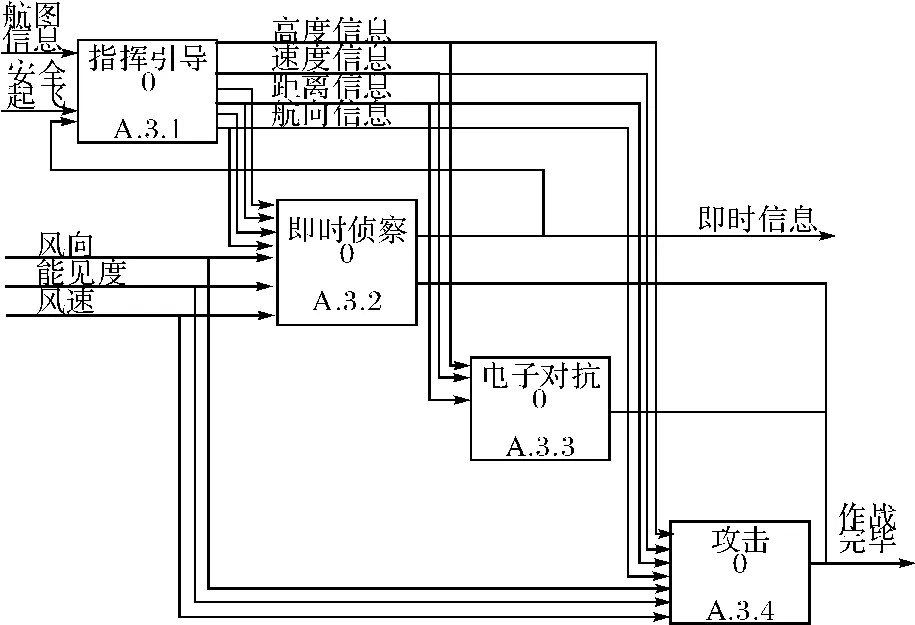
图8 起飞作战子任务分解视图

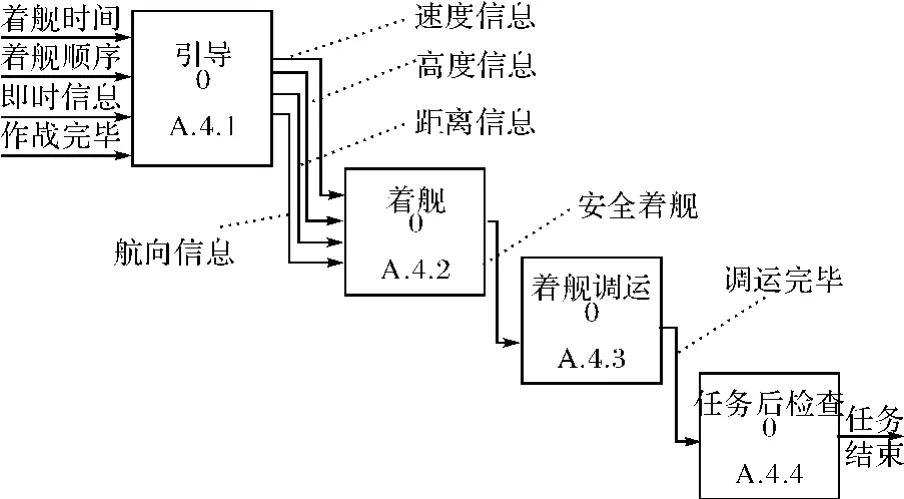
图9 返航回收子任务分解视图

3.1 保障流程集成模型的概念视图

为清楚地显示模型的输入输出关系，作其概念视图，如图10所示。

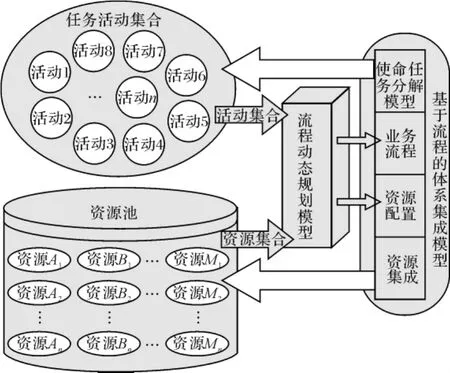
图10 保障流程集成模型的概念视图

保障流程集成模型由三大模块组成，即保障活动TA；保障资源TBi，包括：保障装备TE，保障人员TP和特殊资源TS（空间、备品配件等）；流程动态规划模型。

保障活动TA已经通过保障使命任务分解与建模获得，其参数构成为

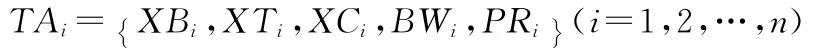
其中XBi为保障资源需求（类型、数量）；XTi为保障活动消耗的时间；XCi为前置后续条件，即要求活动在另一项活动之前或之后才能执行的条件；BWi为保障活动完成次数标记；PRi为活动优先级，即活动在业务流程规划时的优先等级。

保障资源TB是所有保障成员共享的资源，通过信息化系统将体系资源聚合为一体，形成可互换可共享的资源池，供流程动态规划模型统一调配使用。保障资源TB的参数构成为

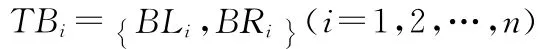
其中BLi为保障资源类型；BRi为保障资源的可用性标记（可用标记为1，不可用标记为0）。

流程动态规划模型的输入是由使命任务分解模型提供的任务活动集合和由资源集成得到的资源集合，其输出是业务流程与资源配置方案，下面介绍具体建模过程。

3.2 流程动态规划模型

用Petri网进行调度属于混合型优化方法［5］，首先以Petri网为工具对系统进行分析、建模，然后利用启发式算法对模型可达图进行搜索，最终获得有效并优化后的调度结果，即业务流程与资源配置方案。

1）Petri网结构模型的建立与简化

时间Petri网分为时间与库所相关联（TPPN）和时间与变迁相关联（TTPN）两种，本文采用TTPN作为建模工具。TTPN为六元组［6］，PN＝（p，T，F，W，M0，D），其 中p＝｛p1，p2，L，pm｝为一个有穷的库所集，用以表示系统中的资源或状态；T＝｛t1，t2，L，tn｝为一个有穷的变迁集，用以代表事件或操作；F⊆（P×T）∪（T×P）为网中的流关系；W：F→｛1，2，3，L｝为一个表示权重的映射函数；M0：P→｛0，1，2，L｝是系统的初始标志；D：P→R＋表示和变迁关联的时间集。在TTPN中，系统的动态行为依赖于变迁的实施序列，而变迁延迟时间的累加即为实施序列的总延迟，因此变迁实施序列是决定系统性能高低的关键因素。

根据保障活动TAi的保障资源需求XBi和前置后续条件XCi，运用Petri网建模工具建立保障活动的Petri网结构模型，如图11所示。

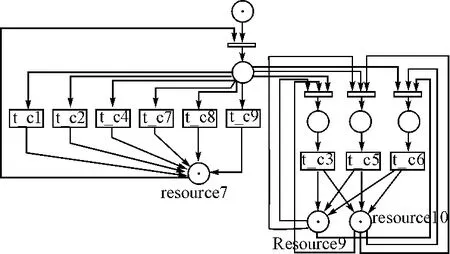
图11 保障活动的Petri网结构模型（部分）

为了进一步简化模型描述，根据模型内部结构具有相似性的特点，采用等价结构压缩技术［7］简化模型描述，得到压缩后的模型如图12所示。如图可见压缩后的模型既保持了子网结构的全部逻辑关系，又显著降低了模型描述的复杂性，有利于对模型结构的理解和仿真程序的设计。

2）调度策略的优先级表达

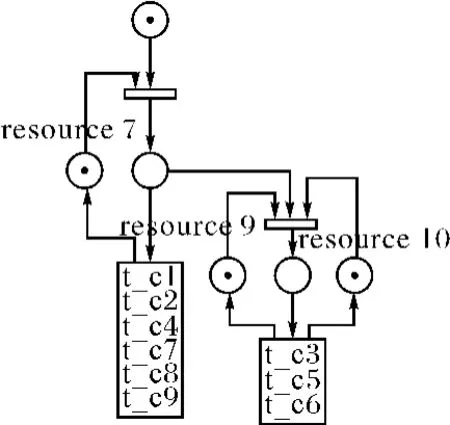
图12 压缩后的保障活动的Petri网结构模型（部分）

调度策略的实质是资源占用的冲突消解，最终目标是给出包含资源最优分配策略的任务活动安排，即最优业务流程。本文提出了一种以优先级表达调度策略的方法，即为每一个变迁赋予一个唯一的优先级标记，在资源占用发生冲突时，比较冲突变迁的优先级，优先级高的变迁得以执行，优先级低的变迁则继续等待。采用优先级表达调度策略的突出优点是计算量极低且具备全局性，有利于提高优化算法的寻优速度和降低启发式算法落入局部最优的可能性，同时也能直观地表达变迁的重要程度，为目标优化提供有益的参考。

3）基于粒子群算法的调度策略优化算法

本文采用粒子群算法来求解最优调度策略，粒子群算法是典型的启发式搜索算法，是解决完全N－P问题的有效方法，适用于非线性、不可微甚至不连续的函数的优化，能以较大的概率求得全局最优解，该算法还具有较强的鲁棒性、全局收敛性和隐含并行性以及广泛的适应性。

粒子群算法的思想是，粒子在解空间中运动，通过跟踪个体极值和群体极值更新个体位置。粒子每更新一次位置，就计算一次适应度值，并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值，更新个体极值和群体极值的位置。

假设在D维空间中，由n个粒子组成的种群X＝（X1，X2，…，Xn）T，其中第i个粒子表示为一个D维的向量Xi＝（Xi1，Xi2，…，XiD）T，其代表该粒子在D维搜索空间的位置，根据目标函数计算每个粒子位置对应的适应度值。第i个粒子速度为Vi＝（Vi1，Vi2，…，ViD）T，其个体极值为Pi＝ （Pi1，Pi2，…，PiD）T，种 群 全 局 极 值 为Pg＝（Pg1，Pg2，…，PgD）T。在每次迭代中，粒子个体极值和群体更新自身的速度和位置公式为

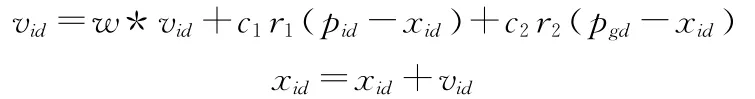
其中，w为惯性权重，d＝1，2，…，D；i＝1，2，…n为当前迭代次数；c1、c2为加速度因子；c1、c2为［0，1］区间随机数。

4 实例

本例中的对岸作战保障任务由38个相关活动构成，保障资源共2类，包括：保障人员8人，其中A类3人，B类3人，C类1人，D类1人；主要紧缺资源有A、B、C三类。首先将与保障任务相关的资源占用情况转化为0－1描述的状态向量，获得的初始状态向量作为流程动态规划模型的初始状态值；然后随机取得优先级向量作为粒子群算法的输入；之后设定迭代次数为300，粒子群数为20，每个粒子的维度为38；最后进行仿真计算，算法迭代过程如图13所示。

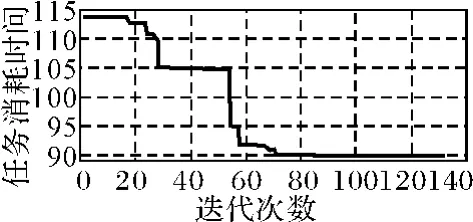
图13 粒子群算法迭代过程

在粒子群算法70次迭代以后，对岸作战保障任务的总时间已经保持不变，模型已经得到了最优解，即对岸作战保障任务最短总时间为89分钟，最终得到最优业务流程如图14所示。

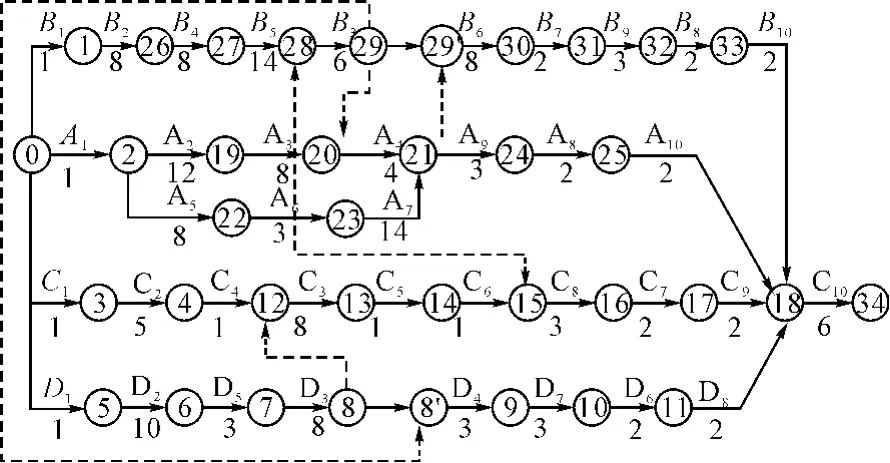
图14 对岸作战保障任务最优业务流程

5 结语

保障使命任务分解与流程集成研究，具有重大的现实意义。本文在目前系统工程主要研究成果基础上，运用美国国防部体系框架（DoDAF），给出了保障使命分解的原则与建立保障任务静态模型的方法，在任务分解的基础上，建立了保障任务静态模型，提出了基于Petri网的保障集成建模方法，给出了模型的概念视图，介绍了流程动态规划模型的建立方法，运用上述模型与方法对实际案例进行分析与应用，验证了模型和方法的有效性，对保障使命任务分解与流程集成研究提供了一种参考，具有现实的支持意义。

［1］宋太亮.装备保障性系统工程［M］.北京：国防工业出版社，2008：2－3.

［2］刘纯贵，陶勇刚.作战飞机多级机务准备流程优化方法研究［J］.航空维修与工程，2006（1）：33－34.

［3］CHEN Jyh－horng，FU Li－chen，LIN Ming－hung.Petri net and GA based approach to modeling，scheduling，and performance evaluation for wafer fabrication［J］.IEEE Trans.Robot.Automat.，2001，17（5）：619－636.

［4］Cebrowski Arthur K.VAdm USN，Garstha John J.Network Centric Warfare：Its Origin an Future.Proceedings of the Naval Institute，1998，124（1）：28－35.

［5］CHEN Hao－xun，IHLOW J，LEHM ANN C.A genetic algorithm for flexible job－shop scheduling［A］.Proceedings of the 1999IEEE International Conference on Robotics ＆ Automation［C］.Detroit：IEEE，1999：1120－1125.

［6］Sun T H，Cheng C W，Fu L C.A Petri net based approach to modeling and scheduling for FMS and a Case Study［J］.IEEE Trans.Ind.Electron，1994，41（6）：593－601.

［7］DoD Architecture Framework Working Group.DoD Architec－ture Framework Version 1.5Volume II［Z］.2007－04－23.