复杂地形对微波超视距雷达传播的影响＊

许庆芬 李洪科 周东瑜

（1.海军七○二厂 上海 200434）（2.海军工程大学电子工程学院 武汉 430033）

1 引言

实际电波传播过程中，其下界面不可能是绝对光滑的平面，无论在军事或者民用方面，电波传播必然会经历复杂地形环境，包括大尺度的不规则地形和小尺度的随机粗糙面。在采样抛物方程传统方法的基础上，针对复杂地形进行抛物方程建模，并结合算例对分段线性地形的抛物方程模型计算，分析地形条件下传播损耗的变化，从而确定地形因素对电波传播特性的影响［1～7］。

2 理论基础

采用傅里叶（Fourier）变换法求解抛物方程，其基本思想是将偏微分方程进行Fourier变换化为常微分方程以方便求解，然后再通过反变换回到原始域。当折射率变化时则不能直接使用Fourier变换。Hardin和Tappert提出了分步解法来处理这一问题［8～9］。

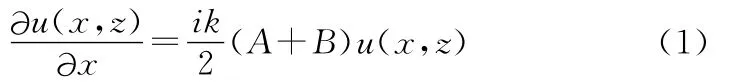
故波函数可表示为

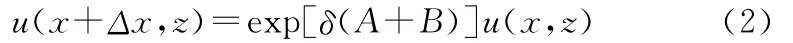
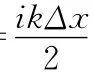
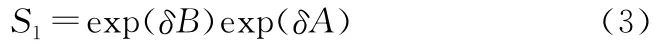
由此式（2）可以写成

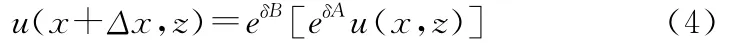
故分步解法可以看作电波通过一系列与传播轴相垂直的相位栅的传播效应，通过用相位栅理论将绕射影响eδA和折射因子eδB分离开来，这就是分步算法的实质。

电波传播特性不仅与电波参数有关，还与大气、地形等环境因素有关［10～12］。抛物方程需要给定相应的边界与初始条件，才能求得唯一场解。所以要研究和分析复杂地形的电波传播特性，必须首先研究复杂地形的电波环境特性，以及复杂地形的电波传播机制和衰减计算方法，并据此正确计算初始场值和设定边界条件。

电波传播的阻抗边界和粗糙边界都满足混合边界条件，下面讨论混合边界条件的数值处理方法。将混合Fourier变换问题离散化，以便进行数值计算，这个过程称为离散混合Fourier变换（DMFT）。首先将计算域高度进行N（N为2的整数次幂）等份离散化

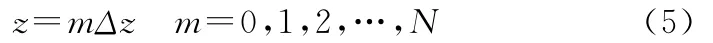
则离散混合Fourier逆变换可表示为

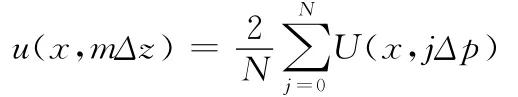
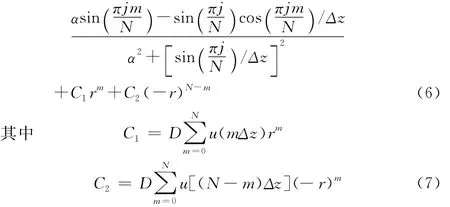
可以将上述FFT算法与抛物方程的步进求解结合起来，从而完成阻抗边界抛物方程的步进求解。DMFT的步骤总结如下：

1）根据天线方向图，利用反Fourier变换求出初始场u（x0，mΔz）；

2）计算出当前距离的辅助函数f（x0，mΔz），并利用式（6）、（7）计算C1和C2；

3）由辅助函数f（x0，mΔz）计算出U（x0，jΔp）；

4）U（x0，jΔp）乘以宽角因子exp（iΔx）实现步进得U（x0＋Δx，jΔp）；

5）C1、C2实现步进，进而求得A（x＋Δx）、B（x＋Δx）；

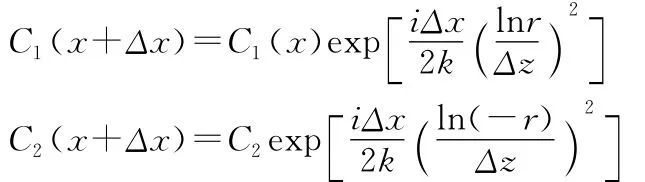
6）对U（x0＋Δx，jΔp）取反Fourier变换得新距离下的辅助函数f（x0＋Δx，mΔz）；

7）利用递归算法求出特解uP（x＋Δx，mΔz），代入公式u（x，mΔz）＝uP（x，mΔz）＋Arm＋B（－r）N－m求得u（x＋Δx，mΔz）；

8）乘以折射因子exp［ik（n－1）Δx］得到下一步步进的场强。

重复利用以上步骤方法，通过该阻抗边界的数值计算方法，理论上便可计算阻抗边界上任意距离和高度的场强分布和传播衰减。

3 数值计算和仿真结果

下面以简化的算例对复杂地形进行仿真分析。以1km的间隔人工抽取距离－高度离散数据对，连接这些数据对构成分段线性地形来近似模拟图1的数字地形，将近似得到的线性高程嵌入抛物方程模型，利用分段线性地形的抛物算法计算传播衰减曲线，通过改变不同天线和环境参数分析其变化对电波传播特性的影响。

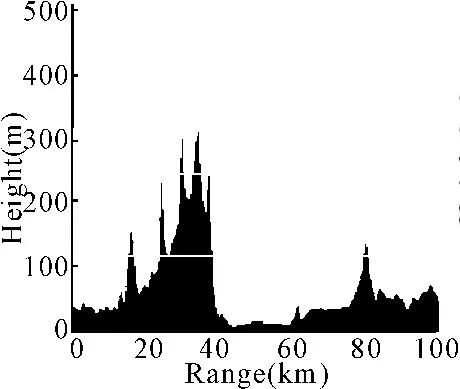
图1 数字地形剖面

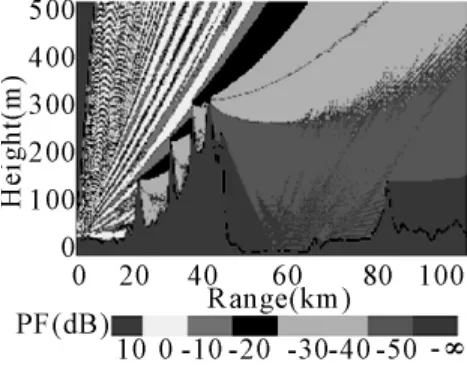
图2 复杂地形的传播因子

算例：电磁参数：高斯天线，水平极化，频率3GHz，仰角0°，天线相对地面高度25m，3dB波束宽度3°；环境参数：标准大气条件，地面近似为理想导体，地形起伏最大高度为300m且出现多刃峰，如图2。此处亦选择300m高度考察电波传播衰减随距离的变化情况。为了便于比较，同时计算平面边界的传播因子。计算平面与地形边界的传播损耗随距离变化的情形，仿真结果如图3和图4所示。

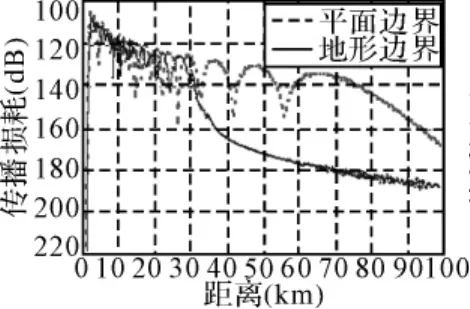
图3 平面与地形边界的传播损耗随距离变化

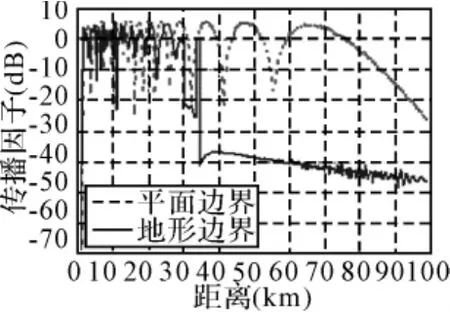
图4 平面与地形边界的传播因子随距离变化

由以上仿真结果可以看出，在30～40km距离之间，电波衰减增大近40dB，这是由于地形的遮蔽作用使得电波能量减少而产生阴影；但是在10～30km距离之间，地形边界的传播衰减总体要小于平面边界的衰减，这主要是反射波引起的，但由于地形的不规则性，其反射波与直射波的干涉效应受到削弱，所以地形边界呈现出相对不规则的振荡。另外说明一点，以上两图分别计算电波传播损耗和传播因子，二者的差别在于前者考虑了自由空间的扩散损耗，而自由空间的电波衰减相对平缓，故在34km距离附近图3较图4的地形衰减曲线略微平滑。

另一方面，分别选取40km和18km距离处的传播因子随高度变化情况。经计算得图5和图6所示结果，为便于比较亦给出相同距离处平面边界的衰减情况。该结果特点有二：其一受地形因素影响衰减比平面边界增大，其二地形曲线随高度的变化梯度较大。根据图1所示的地形剖面，此结果并非偶然，该地形剖面的突出特点是刃峰较多，因而必然在峰顶发生明显的绕射效应，使峰后局部出现传播亮区，亮区以下则是地形遮蔽造成的阴影，由图6可以看出，此处选取的距离正处于34km和16km距离上的两个尖峰之后，尖峰高度分别为307m和153m，所以此距离处的传播因子随高度的变化梯度较大，40km距离处从500m到100m高度衰减增大了50dB，18km距离处从200m～100m高度衰减增大了38dB。

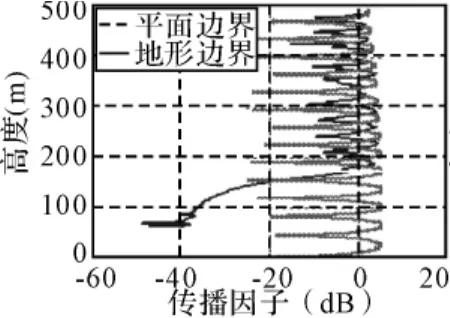
图5 40km距离处传播因子随高度的变化

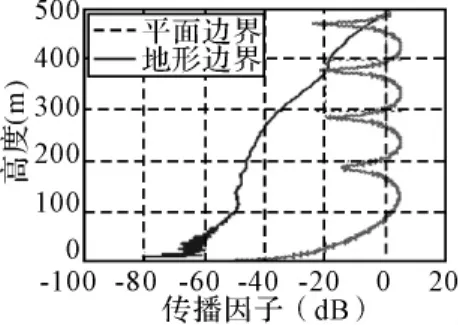
图6 18km距离处传播因子随高度的变化

4 结语

分析电波传播的大气和地形因素，建立了分段线性地形的抛物方程模型，深入研究了阻抗边界的离散混合傅里叶变换以及分段线性地形的边界转换和插值处理，从而可以计算复杂地形环境下任意位置的场强，为电波损耗计算仿真提供理论基础。仿真结果表明，对于随机粗糙面利用阻抗边界进行计算，结果较平面边界有所变化但不敏感。

［1］M.F.Levy.Parabolic Equation Modeling of Propagation over Irregular Terrain［J］.Electronics Letters，1990，26（15）.

［2］Donohue D J，Kuttler J R.Modeling radar propagation over terrain［J］.Johns Hopking APL.Technical Digest，1997，18（2）：54－57.

［3］Barrios A E.Rough surface models implemented within the splitstep parabolic equation algorithm［J］.NRaD Technical Document 2630，1994（4）：100－108.

［4］Piazzi L，Bertoni H L.Effects of terrain on path loss in urban environments for wireless applications［J］.IEEE Trans.on AP.1998，46（8）：1138－1147.

［5］黄麟舒，蒋宇中，王祥书.损耗地面上线天线的一种近似计算方法［J］.海军工程大学学报，2005，17（2）：79－84.

［6］Barrios A E.Rough surface models implemented within the splitstep parabolic equation algorithm［J］.NRaD Technical Document 2630，1994（4）：100－108.

［7］Amalia E.Barrios.A Terrain Parabolic Equation Model for Propa－gation in the Troposphere［J］.IEEE Transactions on Antennas and Propagation，1994，42（1）.

［8］Tappert F D.The parabolic equation method in Wave Propagation in Underwater Acoustics［J］.IEEE，Journal of ocean engineering，1977，25（4）：224－287.

［9］Hardin R H，Tappert F D.Application of the split－step Fourier method to the numerical solution of nonlinear and coefficient wave equations［J］.SIAM Rev，1973，15：419－423.

［10］李方.复杂地形电波传播的抛物方程算法研究［D］.海军工程大学图书馆，2008：44－58.

［11］Ramakrishna Janaswamy.A Curvilinear Coordinate－Based Split－Step Parabolic Equation Method for Propagation Predictions over Terrain［J］.IEEE Transactions on Antennas and Propagation，1998，46（7）.

［12］Piazzi L，Bertoni H L.Effects of terrain on path loss in urban environments for wireless applications［J］.IEEE Trans.on AP，1998，46（8）：1138－1147.