一种基于自适应进化策略采样的粒子滤波算法

党 玲，纪 凯，许江湖

(1.海军大连舰艇学院，辽宁 大连 116018;2.海军工程大学电子工程学院，湖北 武汉 430033)

一种基于自适应进化策略采样的粒子滤波算法

党 玲1，纪 凯1，许江湖2

(1.海军大连舰艇学院，辽宁 大连 116018;2.海军工程大学电子工程学院，湖北 武汉 430033)

提出了一种自适应进化策略算法(AES)，该算法利用适应度值控制变异步长的自适应调整，从而提高了进化策略的搜索效率和精度。将AES算法和粒子滤波(PF)相结合，提出了基于自适应进化策略采样的粒子滤波算法(AESPF)。该算法将AES应用于粒子重采样，以保证粒子的有效性和多样性。通过仿真计算表明，提出的算法可以有效提高滤波性能。

自适应进化策略;重采样;粒子滤波

0 引言

随着计算机运算能力的急剧增长和计算成本的不断降低，粒子滤波(PF)已成为解决非线性、非高斯动态系统的参数估计和状态滤波问题的有效方法［1］。粒子滤波又称序贯蒙特卡罗方法，是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法。粒子滤波完全突破了Kalman滤波理论框架，对系统的过程噪声和量测噪声没有任何限制。

粒子退化是标准粒子滤波算法的主要缺陷。采用重采样方法在一定程度上可以抑制粒子退化现象的发生。而重采样带来的新问题是:权值越大的粒子的子代越来越多，而权值较小的粒子被剔除，最糟糕的情形是新的粒子集实际都是一个权值最大的粒子的子代，即所谓“样本枯竭”现象，从而导致粒子集的多样性变差，不足以用来近似表征后验密度，难以保证估计精度，特别是在样本受限条件下，这种粒子多样性减弱对滤波精度的影响更为突出，甚至导致滤波发散现象［2］。

进化算法(包括遗传算法、进化策略、进化规划)是一种随机搜索优化技术。该算法根据生物中遗传与进化的原理，仿效基因、染色体等物质表达所研究的问题，遵循达尔文“物竞天择，适者生存”原则，使随机生成的初始解通过复制、交换、突变等遗传操作不断迭代进化，逐步逼近最优解。粒子滤波与进化算法的相似之处在于它们都有一个初始化的群体，每个个体代表系统的一个可能解，这些个体均根据一定的规则进行状态转变，对适应度较高的个体进行复制。因此，用进化的思想来解决粒子滤波的退化具有可行性［2］。国内外学者也对此进行了一些努力和尝试［3－9］。在3种进化算法中，遗传算法是一种较为通用的求解方法，而进化策略和进化规划更适宜求解函数优化问题。进化策略还具有收敛速度快、运算简单、易于实现、无需遗传算法复杂的编解码运算等优点［10］。然而在进化策略的应用中，变异步长的选择始终是个棘手的问题。变异步长选择过大，会提高全局搜索能力，但是搜索精度不高;变异步长选择过小，则容易陷入局部极小［11］。为此，本文首先提出了一种自适应进化策略算法(AES)，该算法利用适应度值控制变异步长的自适应调整，从而提高了进化策略的搜索效率和精度。然后将AES算法和粒子滤波(PF)相结合，提出了基于自适应进化策略采样的粒子滤波算法(AESPF)。该算法将AES应用于粒子重采样，以保证粒子的有效性和多样性。通过仿真计算表明，提出的算法可以有效提高滤波性能。

1 粒子滤波

离散时间非线性动态系统的状态方程和量测方程分别为:

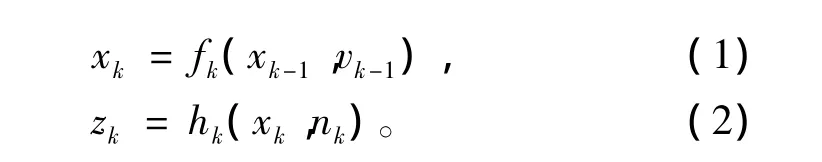
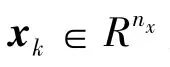
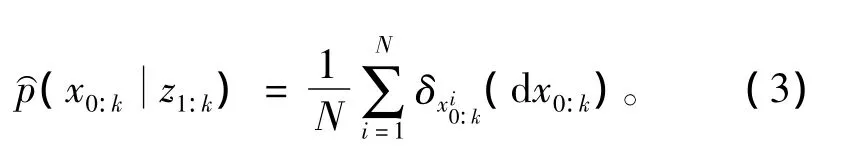
其中:δ(·)为狄拉克函数，则fk(x0:k)的数学期望

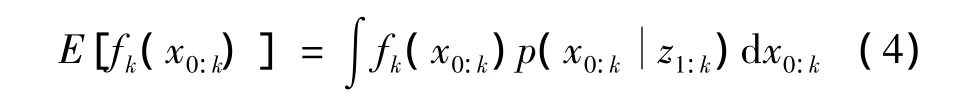
可用如下形式的估计值来逼近:

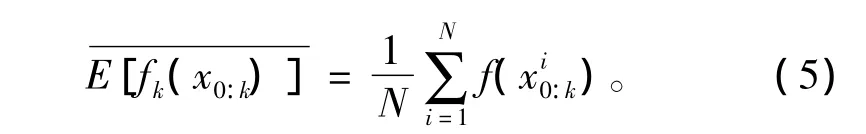
式(5)的收敛性可由大数定律得到保证。然而，通常很难从p(x0:k|z1:k)中直接采样，一种解决方法就是先从1个已知的且容易采样且尽量接近后验概率分布的重要性概率密度函数q(x0:k|z1:k)中采样，并通过对采样粒子进行加权近似

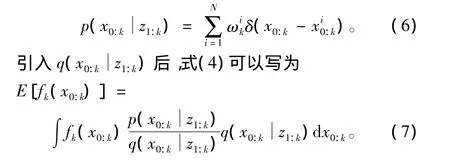
根据贝叶斯公式

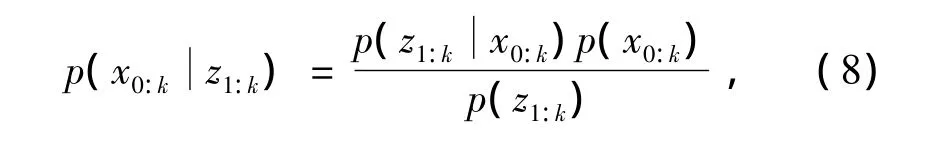
式(7)又可以写为

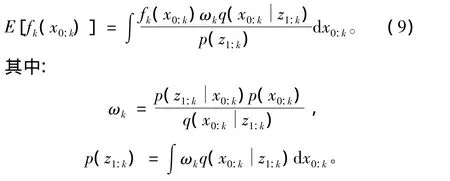
根据蒙特卡罗方法，fk(x0:k)的数学期望可以近似表示为:

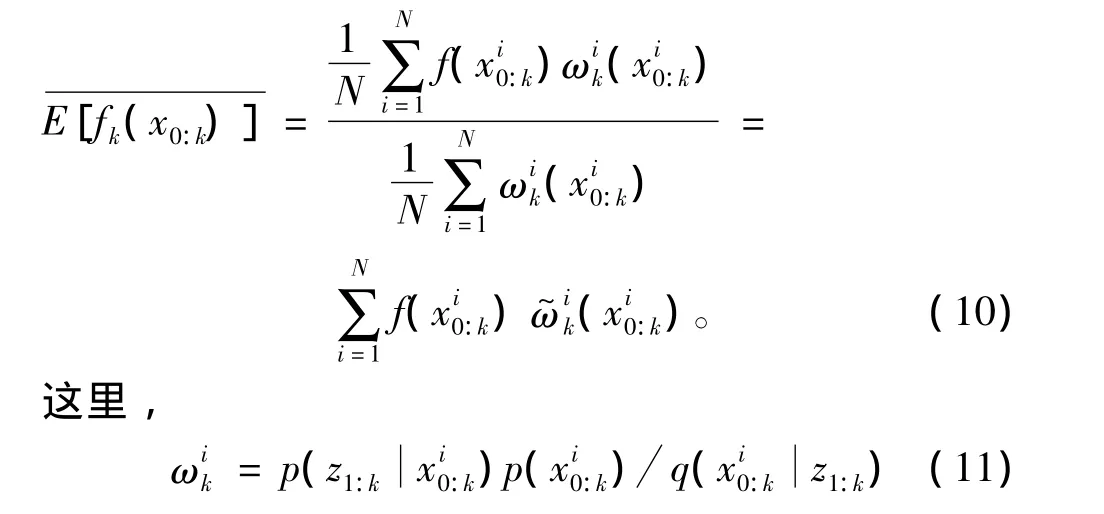
表示每个粒子的权重，ω～ik表示归一化后的权重。将上述原理以递推形式给出，即为序贯重要性采样(SIS)。若将重要性函数写成以下的连乘形式:

假设状态符合Markov过程，在给定状态下，量测条件独立，则可以得出:

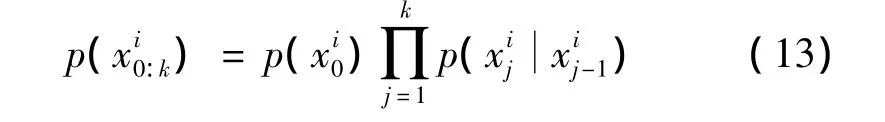
以及

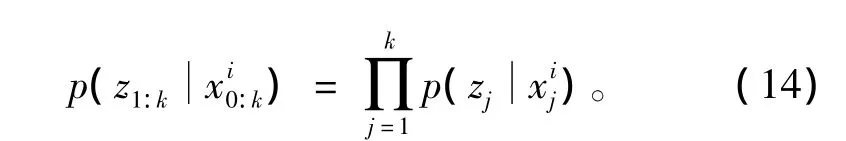
将式(12)～(14)代入式(11)，得到权值的递推公式为

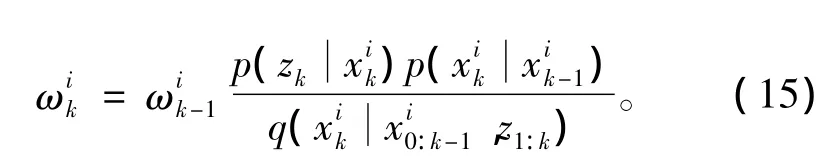
标准粒子滤波算法选择最易于实现的先验概率密度作为重要密度函数

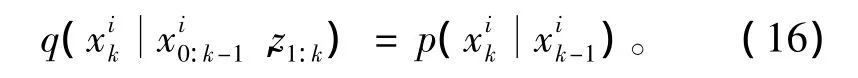
这时，式(15)可以进一步简化为

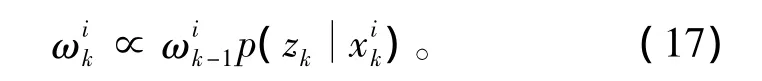
当前时刻粒子的权重被评估后，通过引入重采样技术来改善粒子退化问题。

2 基于自适应进化策略采样的粒子滤波算法

重采样的负作用是样本枯竭，即有较大权值的粒子被多次选择，采样结果包含了许多重复点，从而损失了粒子的多样性，使得描述后验概率密度函数的样本点太少或者不充分。而用进化的思想来解决粒子滤波的退化具有可行性。在3种进化算法中，遗传算法是一种较为通用的求解方法，而进化策略和进化规划更适宜求解函数优化问题。进化策略还具有收敛速度快、运算简单、易于实现、无需遗传算法复杂的编解码运算等优点。然而，在进化策略的应用中，变异步长的选择始终是个棘手的问题。变异步长选择过大，会提高全局搜索能力，但是搜索精度不高;变异步长选择过小，则容易陷入局部极小。为此，下面首先提出一种自适应进化策略算法(AES)，该算法利用适应度值控制变异步长的自适应调整，从而提高了进化策略的搜索效率和精度。然后将AES应用于粒子滤波的重采样中，提出基于自适应进化策略采样的粒子滤波算法。

2.1 自适应进化策略算法

考虑一个连续参数优化问题:

式中，f为适应度函数，S⊆Rn为Rn空间上的闭集。假设种群规模为μ，(Xi(t)，ηi(t))为第t代种群的第i个个体(i=1，2，…，μ)，n维向量Xi(t)=［xi1(t)，xi2(t)，…，xin(t)］，步 长 向 量 ηi(t)=［ηi1(t)，ηi2(t)，…，ηin(t)］，则求解式(18)的 ES步骤为:

1)初始化。产生μ个个体的初始群体，(Xi(t)，ηi(t))(i=1，2，…，μ)，当前代数t=1。

2)适应度计算。计算当前种群中所有个体的适应度值。

3)突变。进化策略的突变是在旧个体基础上添加一个随机量，从而形成新个体:

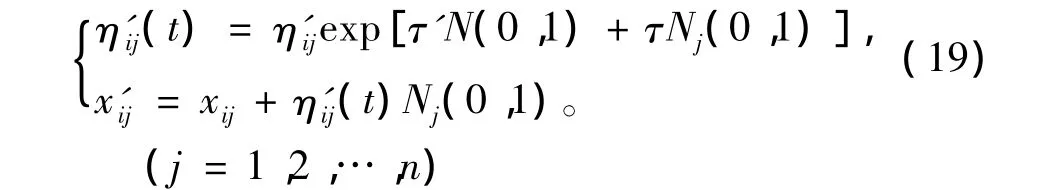
4)选择。进化策略中的选择类似于遗传算法的复制，但是进化策略中的选择是确定型操作，它严格根据适应度的大小，将劣质个体完全淘汰。选择中不采用轮盘法那种随机方式，而是使优质个体100%地保留，劣质个体100%地被淘汰。进化策略的选择有2种:一种为(μ+λ)选择，另一种为(μ，λ)选择。(μ+λ)选择是从μ个父代个体及λ个子代新个体中确定性地择优选出μ个个体组成下一代群体。(μ，λ)选择是从λ个子代新个体中确定性地择优选出μ个个体(要求λ＞μ)组成下一代群体。

从式(19)可以看出，影响进化策略搜索精度和结果的主要是变异步长的选择，变异步长越大，个体变异的幅度越大。增大变异步长，会提高全局搜索能力和搜索效率，但搜索精度会变差;减小变异步长，则会提高搜索精度，但容易陷入局部极小。因此变异步长的大小必须根据搜索过程中的实时要求进行自适应调整。由于适应度反映了个体的目标函数值与最优解的距离，本文通过适应度来控制变异步长的自适应调整:当适应度较大时，说明需要提高精度，应减小变异步长;当适应度较小时，需要扩大搜索范围时，则应增大变异步长。具体调整方法如下:

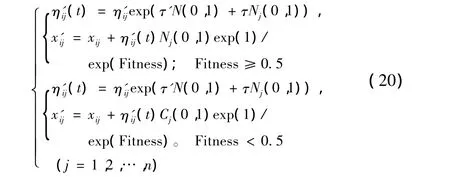
式(20)中，Fitness表示适应度值，为了使算法有效运行，其值控制在0和1之间。C(0，1)表示参数分别为0和1的柯西分布。这里之所以采用柯西分布是由于它比高斯分布产生的随机变量的范围大，从而提高了搜索能力［12］。将式(20)代替式(19)就是本文提出的自适应进化策略(AES)。

2.2 算法步骤

基于自适应进化策略采样的粒子滤波算法步骤如下:

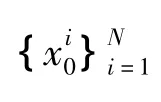
3)自适应进化采样。

①计算每个粒子的适应度值

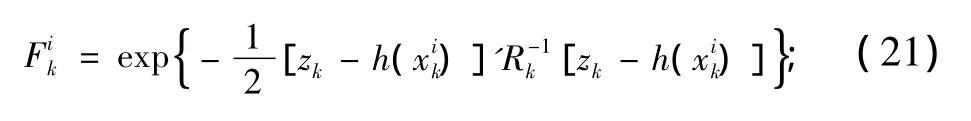
②突变。根据Fik对每个粒子按式(20)进行突变操作。

③选择。计算子代新粒子的适应度值，然后(μ+λ)选择方法进行粒子优选。

3 仿真结果与分析

为了验证本文算法的有效性，通过2个仿真实例比较本文提出的 AESPF，PF以及文献［3］提出的ESPF的滤波结果。

仿真实例1的系统状态方程和量测方程为:

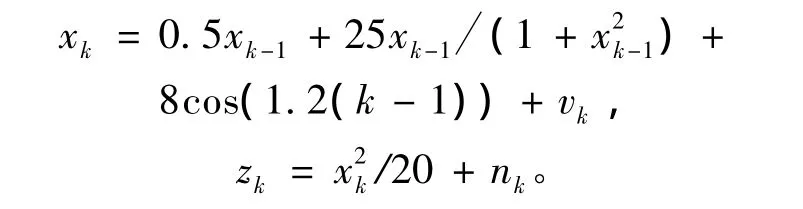
其中，过程噪声和量测噪声均为0均值白高斯噪声，方差分别为10和1。蒙特卡罗仿真次数为50次，仿真步长为60 s，每步采样间隔1 s。表1给出了不同粒子数目情况下，3种滤波算法对实例1的滤波平均均方根误差(RMSE)［13］。

式中:MC为仿真次数;L为仿真长度;x(k)为真实值;x^j(k)为估计值。

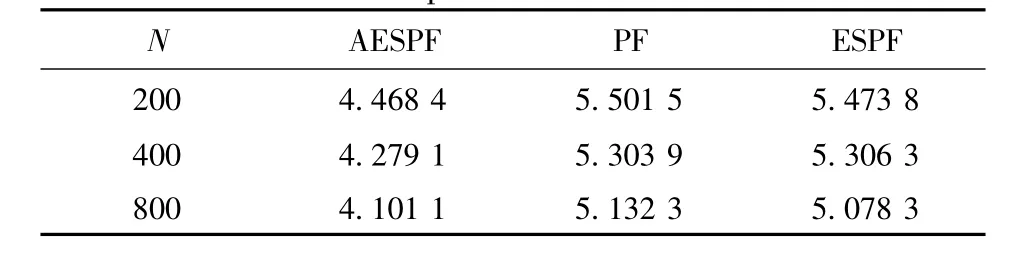
表1 不同粒子数目情况下仿真实例1的平均RMSE比较Tab.1 The mean comparison of RMSE of example 1 for different sample size

从表1给出的数据可知，AESPF的滤波精度明显优于PF和ESPF。

仿真实例2的系统状态方程和量测方程为:

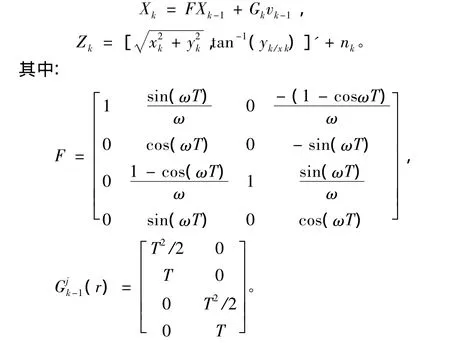
图1和图2分别表示粒子数N取400时，实例2基于X轴方向和Y轴方向目标位置的RMSE曲线。表2分别给出了不同粒子数目情况下，3种滤波算法对实例2的滤波平均RMSE。

从图1和图2看出，本文提出的AESPF无论在收敛速度还是滤波精度都优于PF和ESPF。而综合表1和2的数据可以进一步看出，在高维非线性且粒子数目受限的情况下，AESPF相对于PF和ESPF具有更好的跟踪效果。

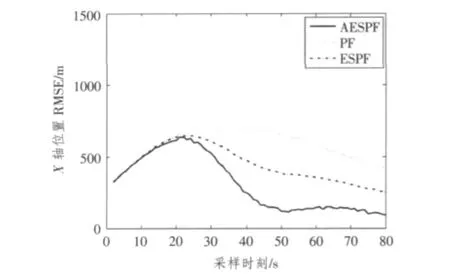
图1 实例2的X轴方向位置RMSE曲线Fig.1 RMSE in position on X axis for example 2

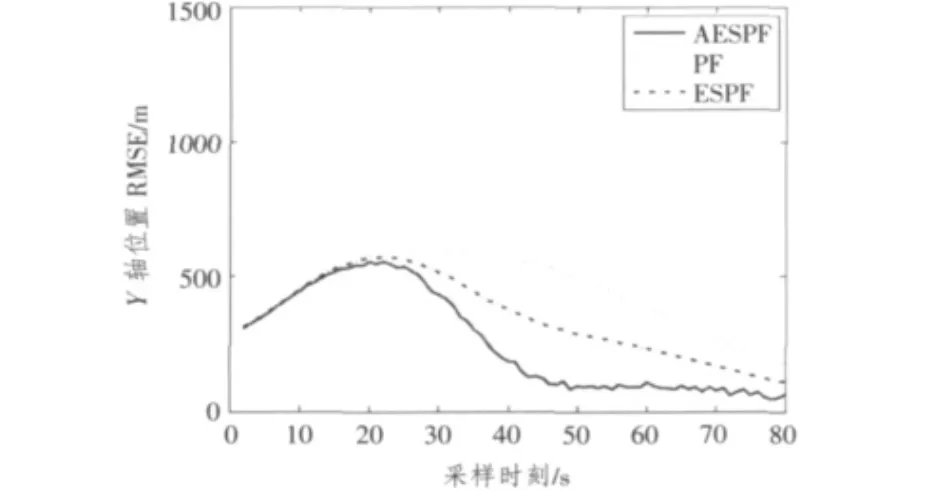
图2 实例2的Y轴方向位置RMSE曲线Fig.2 RMSE in position on Y axis for example 2

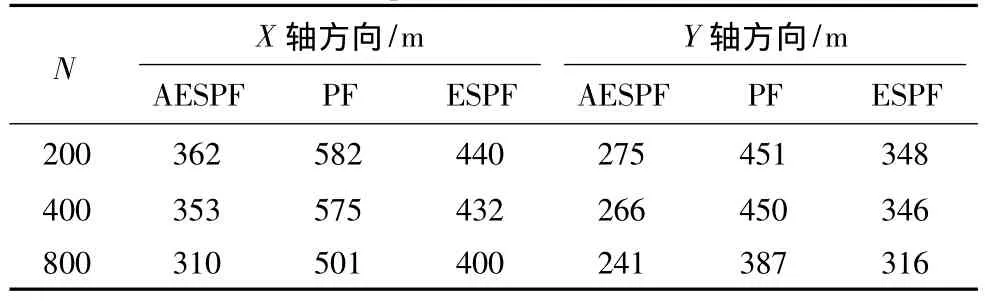
表2 不同粒子数目情况下仿真实例2的位置估计平均RMSE比较Tab.2 The mean comparison of RMSE in position of example 2 for different sample size

4 结语

本文首先提出了一种自适应进化策略算法(AES)，该算法利用适应度值控制变异步长的自适应调整，从而提高了进化策略的搜索效率和精度。然后将AES算法与粒子滤波相结合，提出基于自适应进化策略采样的粒子滤波算法(AESPF)。该算法将AES应用于粒子重采样，以保证粒子的有效性和多样性。最后通过仿真计算表明，提出的算法可以有效提高滤波性能。

［1］GORDON N J，SALMOND D J，SMITH A F M.Novel approach to nonlinear/non-Gaussian Bayesian state estimation［J］.IEE Proceedings－ F，1993，140(2):107 －113.

［2］朱志宇.粒子滤波算法及其应用［M］.北京:科学出版社，2010.

ZHU Zhi-yu.Particle filter algorithms with applications［M］.Beijing:Science Press，2010.

［3］胡振涛，潘泉，梁彦，等.基于进化采样的粒子滤波算法［J］.控制理论与应用，2009，26(3):269 －273.

HU Zhen-tao，PAN Quan，LIANG Yan，et al.The particle filter algorithm based on evolution sampling［J］.Control Theory ＆ Applications，2009，26(3):269 －273.

［4］李翠芸，姬红兵.快速Metropolis-Hastings变异的遗传重采样粒子滤波器［J］.系统工程与电子技术，2009，31(8):1968－1972.

LI Cui-yun，JI Hong-bing.Genetic resampling particle filter based on fast Metropolis-Hastings mutation［J］.Systems Engineering and Electronics，2009，31(8):1968 －1972.

［5］李翠芸，姬红兵.新遗传粒子滤波的红外小目标跟踪与检测［J］.西安电子科技大学学报，2009，36(4):619－644.

LI Cui-yun，JI Hong-bing.IR dim target tracking and detection based on new genetic particle filter［J］.Journal of Xidian University，2009，36(4):619 －644.

［6］RONGHUA L，BINGRONG H.Coevolution based adaptive Monte Carlo localization［J］.International Journal of Advanced Robotic Systems，2004，1(3):183 －190.

［7］叶龙，王京玲，张勤.遗传重采样粒子滤波器［J］.自动化学报，2007，33(8):885 －887.

YE Long， WANG Jing-ling，ZHANG Qin.Genetic resampling particle filter［J］.Acta Automatica Sinica，2007，33(8):885 －887.

［8］PARK S，HWANG J，ROU K，et al.A new particle filter inspired by biologicalevolution:genetic filter［C］.Proceedings of World Academy of Science，Engineering and Technology，Bangkok，Thailand:IEEE，2007，21:459 －463.

［9］UOSAKI k，HATANAKA T.Evolutionstrategiesbased particle filters for fault detection［C］.Proceedings of the IEEE Symposium on Computational Intelligence in Image and Signal Processing.Hawaiian，USA:IEEE，2007，58 －65.

［10］王正志，薄涛.进化计算［M］.长沙:国防科技大学出版社，2000.

WANG Zheng-zhi，BO Tao.Evolutionary computing［M］.Changsha:NationalUniversityofDefenceTechnology Press，2000.

［11］李广文，贾秋玲，刘小雄，等.基于反馈和混沌变异的自适应进化策略［J］.计算机应用研究，2009，26(6):2056－2061.

LIGuang-wen，JIA Qiu-ling，LIU Xiao-xiong，etal.Adaptive evolutionary strategy based on feedback and chaotic mutation［J］.Application Research of Computers，2009，26(6):2056 －2061.

［12］YAO X，LIU Y，LIN G M.Evolutionary programming made faster［J］.IEEE transactions on evolutionary，1999，3(2):82－102.

［13］胡士强，敬忠良.粒子滤波原理及其应用［M］.北京:科学出版社，2010.

HU Shi-qiang，JING Zhong-liang.Particle filter theory with application［M］.Beijing:Science Press，2010.

A particle filter algorithm based on adaptive evolution strategies sampling

DANG Ling1，JI Kai1，XU Jiang-hu2
(1.Dalian Naval Academy，Dalian 116018，China;2.College of Electronics Engineering，Naval University of Engineering，Wuhan 430033，China)

An adaptive evolution strategies(AES)algorithm is first proposed.In the algorithm，Adaptive adjustment of mutation step is controlled by fitness to improve searching efficiency and precision.Then a particle filter based on adaptive evolution sampling(AESPF)is proposed by combining AES and particle filter(PF)，AES is applied to particle resampling to keep the validity and variety of particles in the algorithm.Simulation results indicate the algorithm can effectively improve the filter performance.

adaptive evolution strategies;resampling;particle filter

TB11

A

1672－7649(2012)03－0054－05

10.3404/j.issn.1672－7649.2012.03.011

2011－06－14;

2011－07－07

中国博士后科学基金资助项目(20090461460);湖北省自然科学基金资助项目(2009CDB301)

党玲(1964－)，女，副教授，研究方向为信号与信息处理技术。