基于模糊加权的分布式IMMJPDA算法

党 玲，许江湖

(1.海军大连舰艇学院，辽宁 大连 116018;2.海军工程大学电子工程学院，湖北 武汉 430033)

基于模糊加权的分布式IMMJPDA算法

党 玲1，许江湖2

(1.海军大连舰艇学院，辽宁 大连 116018;2.海军工程大学电子工程学院，湖北 武汉 430033)

提出了一种基于模糊加权的分布式交互多模型联合概率数据互联算法。该算法在融合中心采用模糊加权方法对不同传感器关于同一目标的模型概率、状态估计及其协方差进行融合，而模糊权值为各传感器关于各目标的状态估计协方差的迹的隶属度。最后通过计算机仿真验证了该算法的正确性和有效性。

分布式多传感器多目标跟踪;交互多模型;模糊加权

0 引言

多传感器多目标跟踪是一项备受关注的研究课题，无论在军事领域还是在民用领域，都具有十分重要的理论意义和工程应用价值。多传感器多目标跟踪的关键问题是状态滤波估计和数据互联，其中有效方法主要集中在多模型(MM)算法和联合概率数据互联(JPDA)算法上。

自从文献［1］将交互多模型(IMM)算法和JPDA相结合，提出了IMMJPDA算法后，由于其能较好地解决多目标跟踪中的2个关键问题，即数据互联和状态滤波估计［2］，国内外学者对该算法进行了相当多的研究和改进［3－8］。然而，只有文献［8］提出的基于D－S理论的分布交互式多传感器联合概率数据互联算法可以应用于分布式多传感器多目标跟踪的问题。该算法对每个传感器应用交互式联合概率数据互联法跟踪多目标，并将状态估计、状态估计协方差、模型概率、各模型状态估计、组合新息、新息协方差等虑波结果送至融合中心。融合中心首先对各目标进行航迹关联相关判别并应用D－S证据理论对不同传感器关于同一目标的各模型概率进行融合，然后依此概率计算各目标状态估计并反馈至各传感器使之获得更精确的状态预测。但是研究发现，该算法在对复杂机动目标的跟踪中容易失去对目标的跟踪。为此，本文提出了一种基于模糊加权的分布式交互多模型联合概率数据互联算法(DIMM-MSFJPDA)，该算法在融合中心采用模糊加权方法对不同传感器关于同一目标的模型概率、状态估计及其协方差进行融合，而模糊权值为各传感器关于各目标的状态估计协方差的迹的隶属度。通过仿真计算比较了该算法和基于D－S理论的算法的跟踪性能。结果显示，该算法可以提高跟踪性能，特别是预先设计的模型集合和目标实际机动模式匹配程度不高时。

1 问题描述

假设用q个传感器跟踪杂波环境中的N个目标，模型集合为 M={m1，m2，…，mJ}，J表示模型集合的长度。对于模型集合M中第j个模型，目标r的状态和量测方程为:

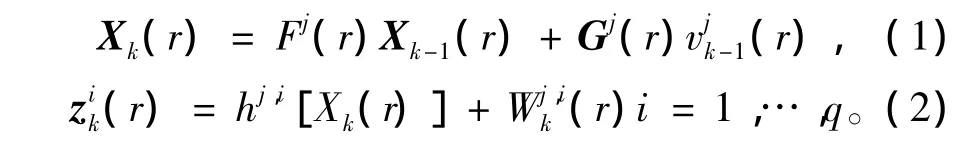
2 基于模糊加权的分布式交互多模型联合概率数据互联算法

分布式多传感器系统中，各传感器将各自的滤波结果传送至融合中心进行融合处理。本文提出的DIMM-MSFJPDA对各传感器应用单传感器的IMMJPDA算法，并将各目标基于模型的状态估计及其相对应的估计协方差阵，模型概率送至融合中心进行航迹关联。在融合中心，首先对这些滤波结果进行关联判决，然后采用基于模糊加权的方法对各传感器对应于同一目标的模型概率、基于各模型的状态估计及其协方差阵进行融合，从而得到各目标的总体状态估计及其相应的估计协方差阵，而模糊权值为各传感器关于各目标的状态估计协方差的迹的隶属度。最后，将各目标的总体状态估计反馈至各传感器以期获得更为精确的状态预测。

设在k时刻第 i个传感器传送至融合中心关于目标r的信息向量为

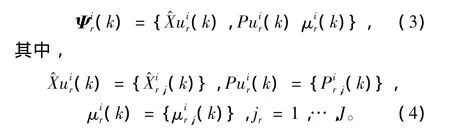
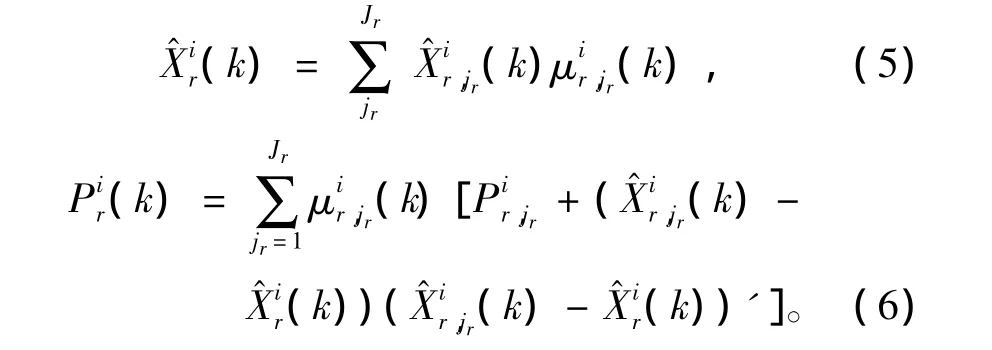
对于已经确认为关于同一目标的信息向量，融合中心采用模糊加权方法对不同传感器关于同一目标的模型状态估计，相应的估计协方差阵，模型概率进行融合。由于各传感器关于各目标的状态估计协方差阵(由式(6)计算)反应了该传感器对该目标的滤波精度，而滤波精度应该决定该传感器对目标的状态估计、协方差阵和模型概率在融合中心进行融合时的权重。因此这里的模糊加权方法将各传感器关于各目标的状态估计协方差阵的迹看作1个模糊集中的元素，迹的大小将决定隶属度的大小，而隶属度由模糊集的隶属函数映射而得。这里的隶属函数定义为:

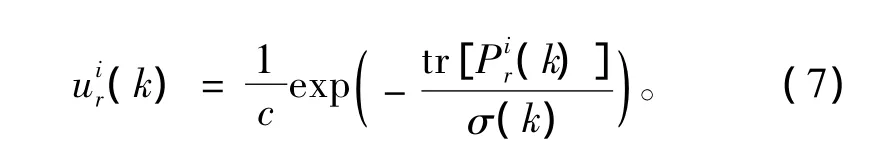
式中:c为归一化因子;σ(k)为尺度参数。定义分别为

令k时刻融合中心对目标r基于模型j的状态估计、相应的估计协方差阵，模型概率分别为 X^r，j，Pr，j和 μr，j，则有

利用式(10)～式(12)的计算结果，可得融合中心对目标r的总体状态估计及相应的状态估计协方差阵:最后融合中心将X^r，j(r=1，…，N;j=1，…，J)反馈至各传感器，以期获得更为精确的状态预测。

3 计算机仿真

为了验证本文算法的有效性，通过杂波环境下对2个强机动目标的跟踪来比较本文算法和基于D－S理论的分布交互式多传感器联合概率数据互联算法(DIMM-MSDSJPDA)的性能。仿真中采用的机动模型为协同转弯模型［9］，这样式(1)中:

目标1的初始状态为［31851，－8.3，28638，－ 399.9］'，机动想定为:在1 ～ 40 s，56 ～ 75 s，88 ～130 s，目标1作匀速直线运动;在41～55 s，76～87 s，目标1分别作了2个转弯，转弯速率分别为－ 8.6，5.7°/s。

目标 2的初始状态为［47240，－380，4712，124.9］'，机动想定为:在1 ～ 70 s，91 ～ 130 s，目标1作匀速直线运动;在71～90 s，目标2作了1个转弯，转弯速率为 －4.3°/s。2个目标的机动航迹如图1所示。

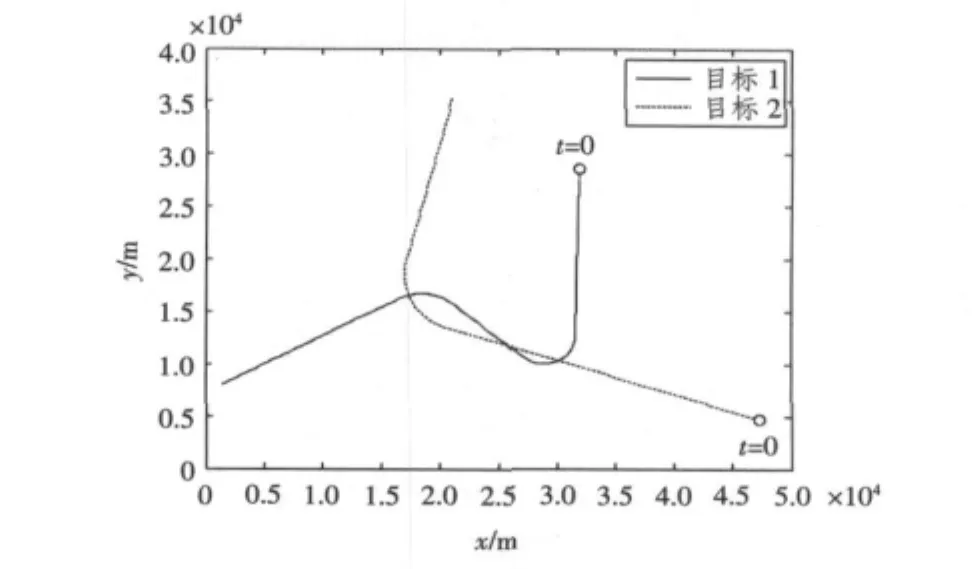
图1 目标航迹图Fig.1 The true trajectories of the targets

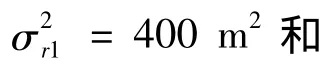
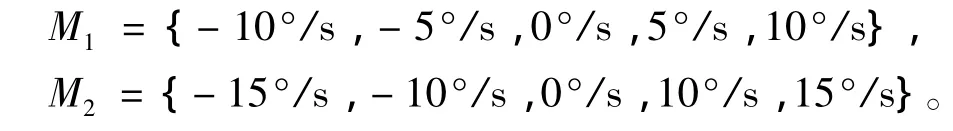
显然，M1比M2更匹配目标的实际机动模式。

为了比较2种算法的性能，将进行50次Monte Carlo仿真后的位置和模型估计均方根误差。而k时刻模型估计均方根误差的定义为［10］:

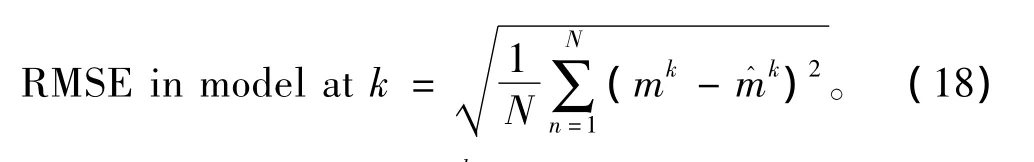
式中:N为仿真次数;mk为目标真实的机动模式;m^k为估计的机动模型，其定义为:

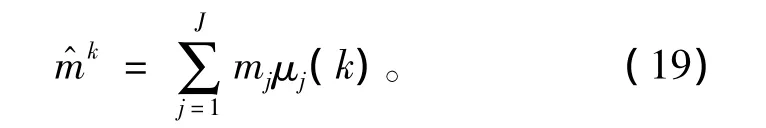
其中:μj(k)为k时刻模型mj的模型概率。由于模型mj(j=1，…，J)是预先确定的，因此模型估计均方根误差反映了多模型算法为了匹配目标真实机动模式而调整其模型概率的准确性，从而也从另一个方面反映了多模型算法的跟踪性能。

进行50次Monte Carlo仿真。图2和3分别为DIMM-MSFJPDA、DIMM-MSDSJPDA采用模型集合M1时对目标1和目标2滤波的位置均方根误差;图4和图5则分别是采用模型集合M2时对目标1和目标2滤波的位置均方根误差;图6和图7分别是对目标1和目标2的模型估计均方根误差。

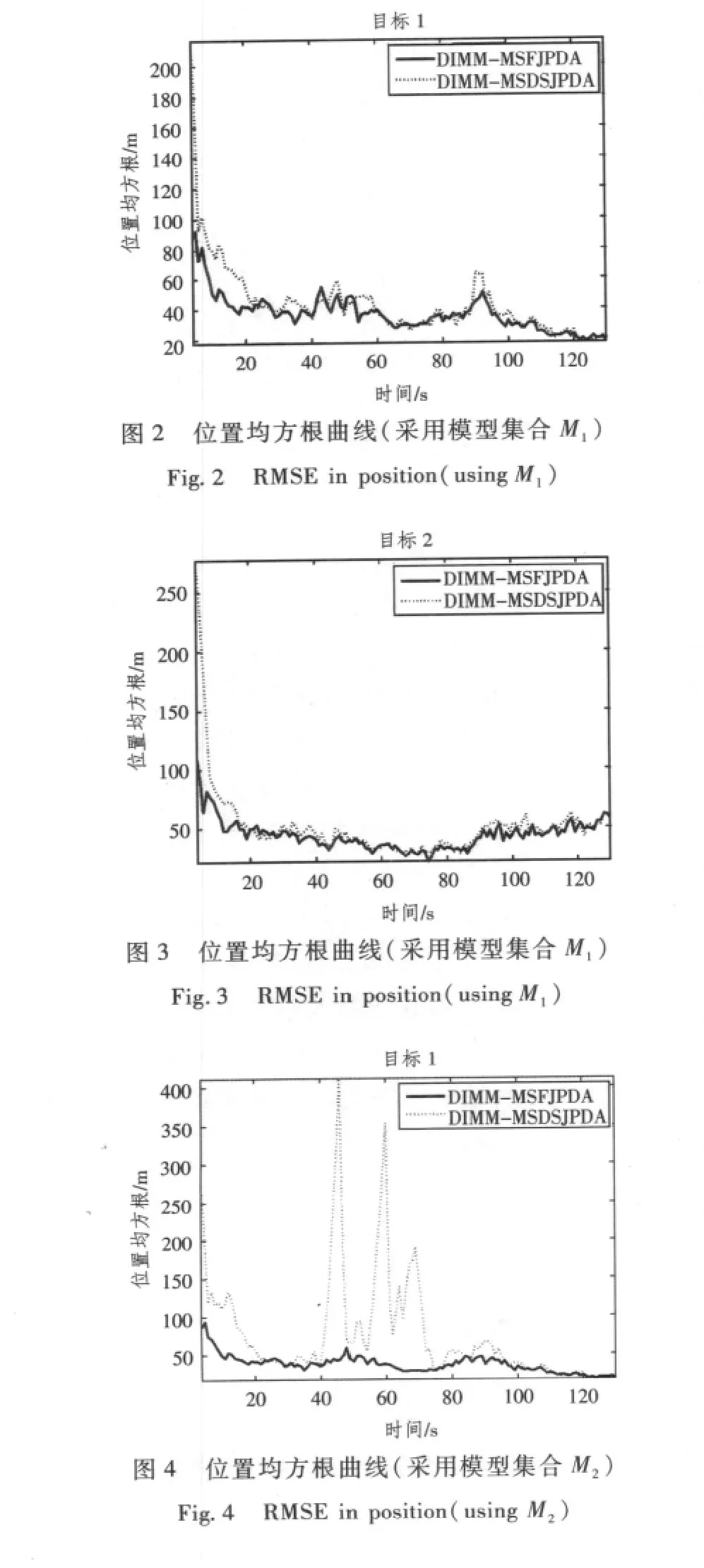
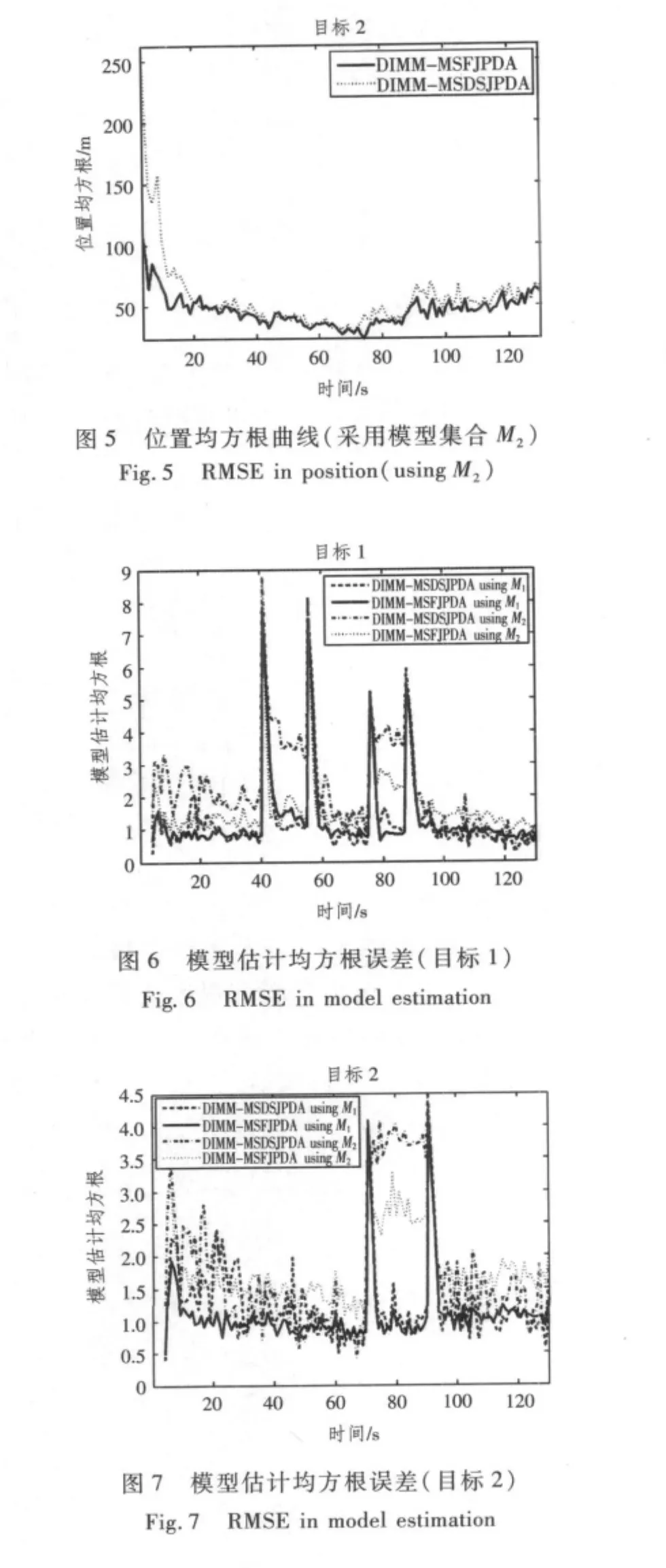
从图2和图3可以看出，当采用模型集合M1时，DIMM-MSFJPDA对2个目标的跟踪性能略好于DIMM-MSDSJPDA。从图4和图5可以看出，当采用模型集合M2时，DIMM-MSFJPDA对2个目标的跟踪性能明显优于DIMM-MSDSJPDA。图6和图7进一步说明了上述事实。

4 结语

本文提出了一种基于模糊加权的分布式交互多模型联合概率数据互联算法(DIMM-MSFJPDA)，该算法在融合中心采用模糊加权方法对不同传感器关于同一目标的各模型概率进行融合，而模糊权值为各传感器关于各目标的状态估计协方差的迹的隶属度。通过仿真计算比较了该算法和基于D－S理论的分布交互式多传感器联合概率数据互联算法的跟踪性能。结果显示，该算法可以提高跟踪性能，特别是在预先设计的模型集合和目标实际机动模式匹配程度不高时。

［1］De FEO M，GRAZIANO A，MIGLIOLI R，et al.IMMJPDA versus MHT and Kalman filter with NN correlation:performance comparison［J］.IEE Proc-Radar Sonar Navig.，1997，144(2):49 －56.

［2］李辉，沈莹，等.交互式多模型目标跟踪的研究现状及发展趋势［J］.火力与指挥控制，2006，31(11):1 －4.

［3］CHAN B，TUGNAIT J K.Tracking of multiple maneuvering targets in clutter using IMM/JPDA filtering and fixed-lag smoothing［J］.Automatica，2001，37:239 －249.

［4］TUGNAIT J K.Tracking of multiple maneuvering targets in clutter using multiple sensors，IMM，and JPDA coupled filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，2004，40(1):320 －330.

［5］PURANIK S，TUGNAIT J K.Tracking ofmultiple maneuvering targetsusingmultiscan JPDA and IMM filtering［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(1):23 －35.

［6］张晶炜，熊伟，何友.集中交互式多传感器联合概率数据互联算法［J］.光电工程，2006，33(11):26 －30.

［7］张晶炜，何友，熊伟.集中交互式多传感器模糊联合概率数据互联算法［J］.电子学报，2008，36(8):1655 －1659.

［8］张晶炜，修建娟，何友，等.基于D－S理论的分布交互式多传感器联合概率数据互联算法［J］.中国科学(E辑:信息科学)，2006，36(2):182 －190.

［9］LI X R，BAR-SHALOM Y.Design ofan interacting multiple model algorithm for tracking in air traffic control systems［J］.IEEE Transactionson ControlSystems Technology，1993，1(3):186 －194.

［10］LI X R，ZHANG Y M.Multiple-model estimation with variable structure part V:likely-model set algorithm［J］.IEEE Transactions on Aerospace and Electronic Systems，2000，36(2):448 －466.

Distributed interacting multiple model joint probabilistic data association algorithm based on fuzzy weighted method

DANG Ling1，XU Jiang-hu2

A distributed interacting multiple model joint probabilistic data association algorithm based on fuzzy weighted method is presented in this paper.The model probabilities，state estimation and its covariance of same target corresponding to different sensors are fused in the fusion centre using fuzzy weighted method in the algorithm.The fuzzy weight is membership degree of trace of covariance of same target corresponding to different sensors.The validity and effectivity of the algorithm are tested by computer simulation.

distributed multisensor multitarget tracking;interacting multiple model;fuzzy weight

TN957

A

1672－7649(2012)04－0067－04

10.3404/j.issn.1672－7649.2012.04.015

2011－11－19;

2011－12－05

中国博士后科学基金资助项目(20090461460)

党玲(1964－)，女，副教授，研究方向为信号与信息处理技术。

(1.Dalian Naval Academy，Dalian 116018，China;2.College of Electronics Engineering，Naval University of Engineering，Wuhan 430033，China)