发电用燃气轮机动态性能仿真

栾永军，孙 鹏，李东明，俞世康，董 斌

(中国船舶重工集团公司第七○三研究所，黑龙江 哈尔滨 150078)

发电用燃气轮机动态性能仿真

栾永军，孙 鹏，李东明，俞世康，董 斌

(中国船舶重工集团公司第七○三研究所，黑龙江 哈尔滨 150078)

针对发电用燃气轮机，基于Matlab/Simulink仿真平台构建其仿真模型。使用仿真模型，计算在电网负荷波动以及机组甩负荷的情况下燃气轮机的动态特性。参照电网指标，通过优化控制策略，给出电网负荷变化时燃气轮机的响应特性。

燃气轮机;发电;仿真

0 引言

燃气轮机作为供能设备已广泛应用于诸多领域，尤其用作发电动力设备，无论是军用还是民用，装机数量逐渐增多。当燃气轮机用于发电时，其输出转速为恒定值。当电网负荷波动或机组甩负荷时，燃气轮机输出转速需快速稳定回恒定值，以防电力系统输出频率长时间内不稳定而造成用电设备损坏。

本文建立某型燃气轮机用作发电时的仿真模型，通过模型仿真计算结合我国电网指标，给出电网负荷变化时燃气轮机的响应特性。

1 发电控制策略

为确保电网负荷波动或机组甩负荷时，燃气轮机输出转速能快速稳定回恒定值。转子平衡方程式为:

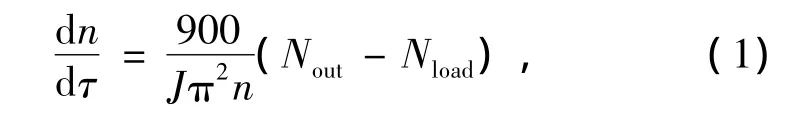
式中:n为输出转速;Nout为输出功率;Nload为电网功率;J为转动惯量。

参照式(1)可分析得出:

当Nload减少或为0时，dn/dτ＞0，输出转速上升，为使n快速稳定到恒定值，需迅速降低输出功率Nout。迅速降低Nout可通过快速降低工质燃气的总焓实现。降低燃气总焓，有2种方法:一是减少用于燃烧的空气量;二是减少喷入燃烧室内的燃油量。为实现快速降低总焓的目标，需2种方法综合作用。实现手段为在压气机后设有放气阀用于放空气，在燃料系统需装备调速器用于根据转速变化快速切油并且保障燃烧室内不会发生贫油熄火。

当Nload增大时，dn/dτ＜0，输出转速降低，为使n快速稳定到恒定值，需迅速增加喷入燃烧室内燃油量进而增加输出功率Nout。迅速增加Nout，需防止快速增加喷油量而导致的富油熄火，还要防止燃气温度过高触发涡轮叶片的超温保护进而导致机组故障停机。

因此，为使燃气轮机输出转速能快速稳定回恒定值，需针对上述分析开展燃气轮机动态性能仿真研究，并通过相应控制策略实现。

2 建模方法

基于容积惯性法建立燃气轮机非线性仿真模型，该方法避免了微分方程右函数计算中的迭代，简化了仿真计算流程，提高了模型的灵活性和通用性。

在建模过程中，将燃机看作由压气机、涡轮等转动部件和包括燃烧室在内的流动连接段串联而成。连接压气机和涡轮的转轴建立了机械联系，而流动连接段则基于容积惯性建立了各转动部件间的气动关系。容积惯性法示意图如图1所示。

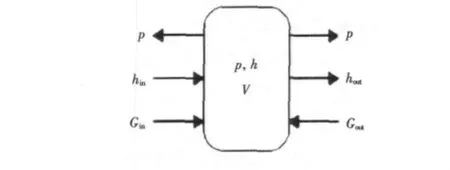
图1 容积惯性法示意图Fig.1 Schematic drawings of volume inertia

假定容积内压力均匀，用1个集总压力p来表示，做功流体为理想气体，忽略流体间的动量。质量守衡如下式:

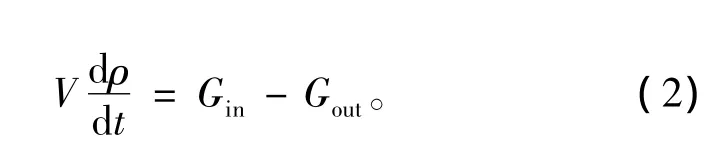
式中:ρ为容积中气体密度;V为容积体积;Gin为流经容积进口截面的气体的质量流量;Gout为流经容积出口截面的气体的质量流量。

将工质近似为理想气体处理，有

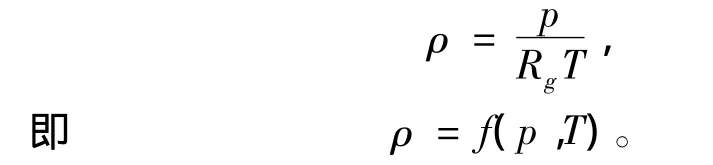
因此，式(2)化为:

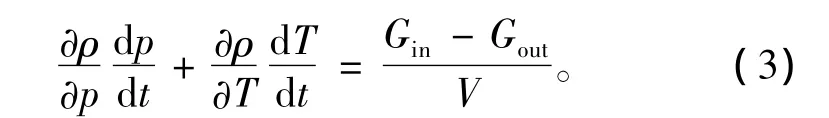
对于纯容积连接段，忽略容积内工质同外界的传热及进出口的压差，有

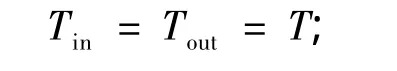
又因为

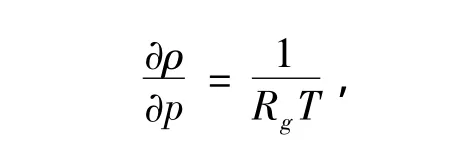
式(3)可化简为:

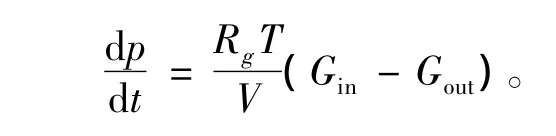
式中:p，T，Gin，Gout，分别为纯容积连接段内压力，温度，进、出口工质的质量流量;Rg为工质的气体常数。

3 数学模型

基于容积惯性法，建立燃气轮机部件数学模型以及部件间匹配原则。

3.1 压气机模型

已知压气机输入端参数(入口压力Pin，出口压力Pout，入口温度Tin，转速n)，计算输出端参数(入口空气流量Gin，出口空气流量Gout，出口温度Tout，消耗功率NC)的步骤如下:

1)π =Pout/Pin，π为压气机压比;

3)(Gz，η)=f(π，nz)，Gz为入口空气折合流量，η为压气机绝热效率，f可通过压气机特性曲线求解;

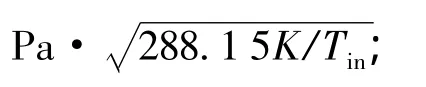
5)Gin－Gcq=Gout，Gcq为压气机抽出的空气流量;

6)由物性计算可得:

入口比焓 Hin=f(Tin，0)，入口熵函数 ψin=f(Tin，0)，理想熵函数 ψ2，i= ψin+lgπ，由二分法求出 T2，i，H2，i=f(T2，i，0);

比功 wC=(H2，i－ Hin)/η;

出口比焓Hout=Hin+wC，出口温度由二分法求出 Tout=f(Hout，0);

7)消耗功率

NC=Gin·wC－ Gcq·wcq，Gcq·wcq为压气机因抽气而少消耗的功率;

对于不同的压气机模型，只需进行更换特性曲线及设置抽气情况等操作即可。

3.2 涡轮模型

已知涡轮输入端参数(入口压力Pin，出口压力Pout，入口温度Tin，转速n)，计算输出端参数(入口空气流量Gin，出口空气流量Gout，出口温度Tout，输出功率NT)的步骤如下:

1)π =Pin/Pout，π为涡轮膨胀比。

3)(Gz，η)=f(π，nz)，Gz为入口燃气折合流量，η为涡轮绝热效率，f可通过涡轮特性曲线求解。

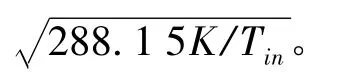
5)Gin+gch，2=Gout，gch，2为非入口导叶处引入的冷却涡轮叶片空气量。

6)由物性计算可得:

入口比焓Hin=f(Tin，f)，入口熵函数ψin=f(Tin，f)，理想熵函数 ψ2，i= ψin－ lgπ，由二分法求出 T2，i，H2，i=f(T2，i，f);

比功 wT=(Hin－ H2，i)·η;

出口比焓Hout=Hin－wT，出口温度由二分法求出 Tout=f(Hout，f)。

7)输出功率NT=Gout·wT。

8)需要注意的是，计算中的Tin实际上并不等同于前一部件出口的温度，而是涡轮入口导叶气流掺混后的温度，即

式中:f－1代表二分法由比焓求温度。

9)gch，1+gch，2=Gcq－ gfq，其中:gch，1为涡轮入口导叶处掺混空气量;gch，2为涡轮其他注气位置掺混;gfq为压气机中放气量;Gcq为压气机中抽气量。

10)物性计算步骤6)中，变量f为油气比;当有冷却空气掺混时，涡轮模型进出口油气比有差异。

11)对于不同的涡轮模型，只需进行更换特性曲线及设置注气掺混情况等操作即可。

3.3 纯流动连接段模型

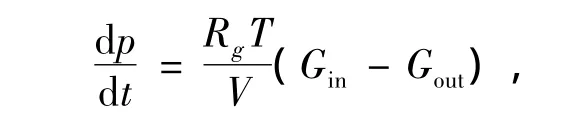
式中:Rg为工质的气体常数。

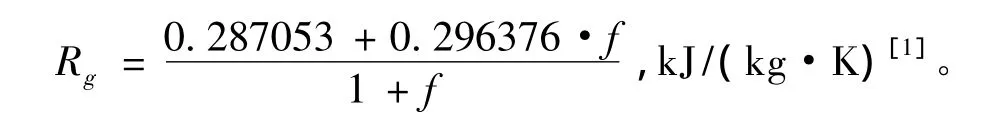
当工质为空气时，油气比f为0。

3.4 燃烧室模型

燃烧室模型可看成是纯流动连接段模型和燃烧放热模型，燃烧放热模型基于下式:

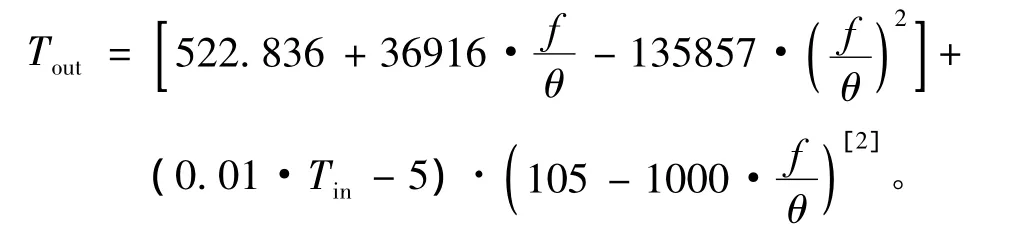
式中:Tin为燃烧室入口空气温度;Tout为燃烧室出口燃气温度;f为油气比;θ=41613/(η·Hu)为修正系数，η为燃料的完全燃烧系数，Hu为燃料低热值。

3.5 转子模型

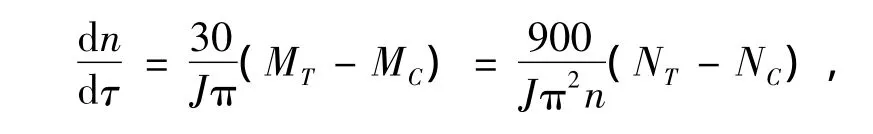
式中:n为转子的转速，r/min;J为为转子的转动惯量，kg·m2;NT为涡轮输出功率，W;NC为压气机消耗功率，W。

3.6 放气模型

进行放气时，数学模型如下:

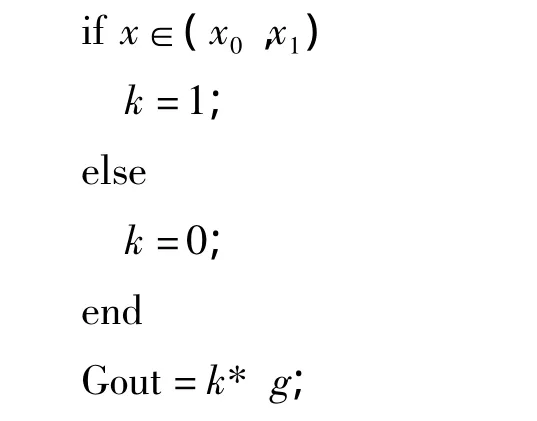
值域(x0，x1)代表某种放气机制，g为放气量，Gout为实际放气效果。当参数x满足放气机制时，输出k=1，实现放气;不满足时则输出k=0，不放气。

3.7 调速器模型

调速器主要由调速控制器与调速执行器2部分组成，输入为给定转速与反馈转速，经比较后送控制器(P，PD，PI或PID)运算后输出油门位置给定值，再经执行器放大后输出油门位置信号至喷油泵。根据其各元部件之间的相互关系可分解为如图2所示的模块结构。

图2 调速器模块化结构Fig.2 Modularized model of speed controller

3.8 部件匹配原则

当燃气轮机发电模块稳定运行时，部件间的匹配需满足如下原则:

1)压气机与涡轮的功率平衡，即高、低压涡轮的输出功率×机械效率－附件耗功=高、低压压气机消耗功率;

2)压气机与涡轮的转速平衡，即高、低压压气机转速=高、低压涡轮转速;

3)流经整个燃气轮机发电模块原动机的质量流量平衡，即压气机入口空气流量+燃油流量－放气量=涡轮出口燃气流量;

4)压气机增压比与涡轮膨胀比的平衡，即增压比×压力恢复系数=膨胀比;

5)动力涡轮与负荷的平衡，动力涡轮输出功率×机械效率=负荷消耗功率。

4 仿真模型

依据已建立的数学模型，构建某型发电用燃气轮机仿真模型，部件模型如图3～图9所示。

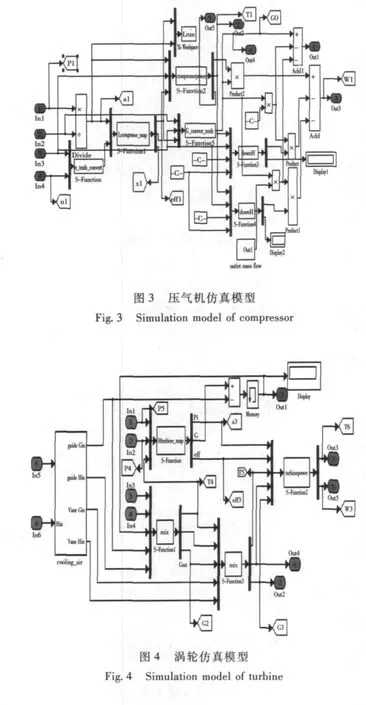
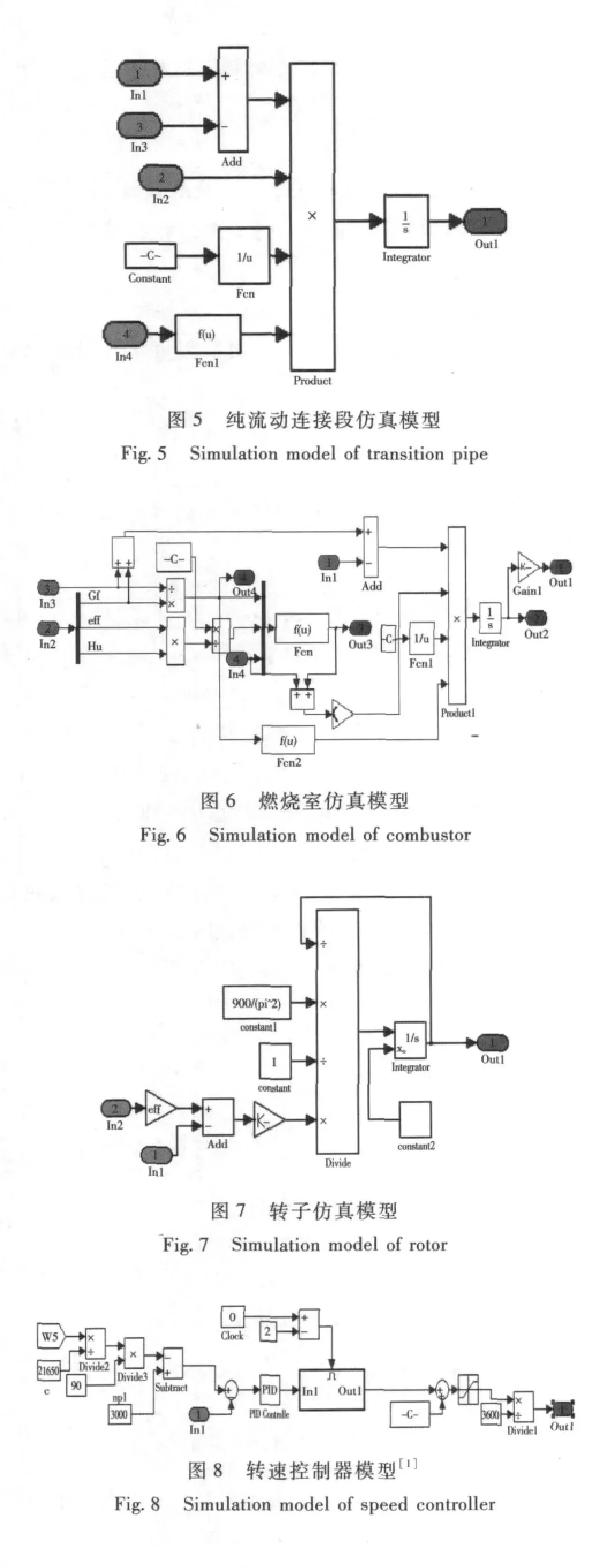
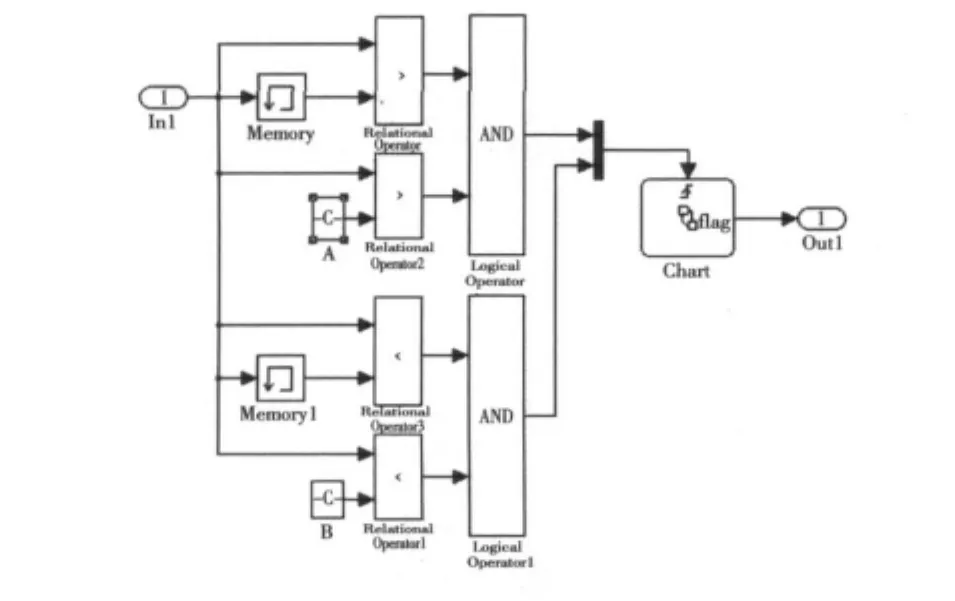
图9 放气阀模型Fig.9 Simulation model of bleed value

5 计算结果

使用仿真模型和已制定的控制策略，对某型发电用燃气轮机动态特性进行计算。

1)电网负荷由额定工况突降4 MW，而后增至额定工况。

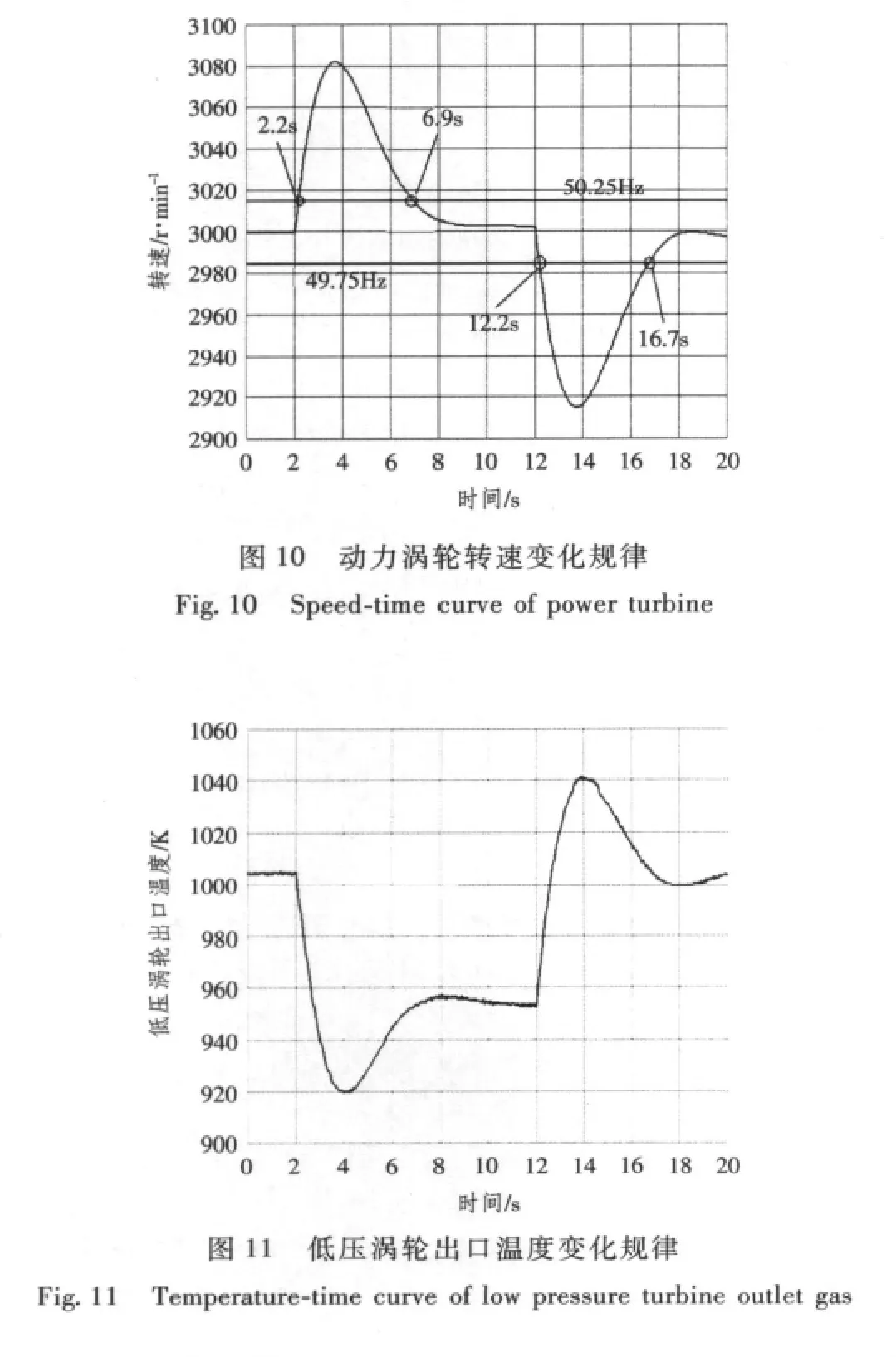
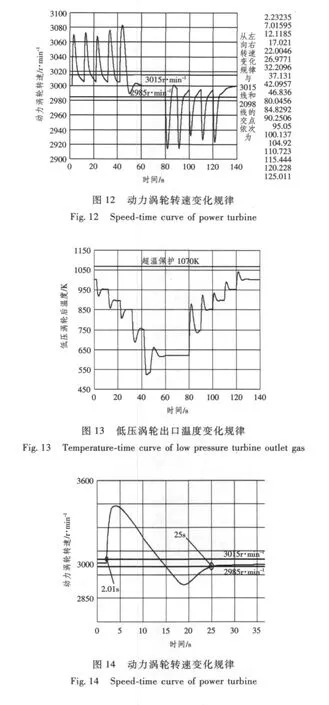
2)电网负荷连续增减4 MW

由计算结果可看出，负荷突增4 MW，4.5 s稳定回3 000 r/min±0.5%，瞬态调速率2.8%;负荷突减4 MW，4.7 s可稳定回3 000 r/min±0.5%，瞬态调速率2.8%。

由计算结果可看出，负荷连续突增、突减，在不同的负荷功率等级条件下，动力涡轮转速稳定到3 000 r/min±0.5%所需的最短时间为4.72 s，最长稳定时间为4.97 s，瞬态调速率最大值为3.3%。

3)机组甩负荷

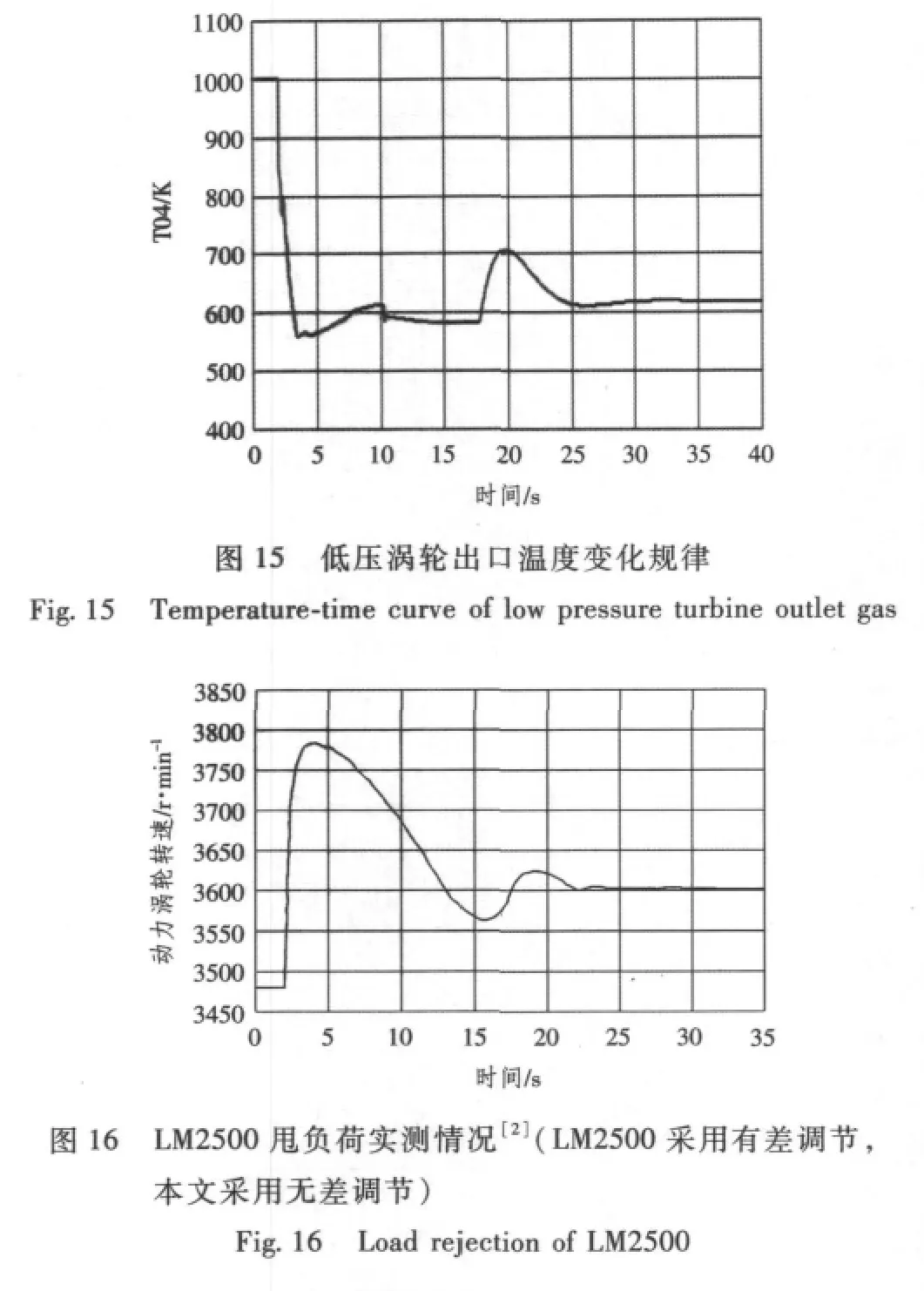
由计算结果可看出，机组甩负荷，22.99 s稳定回3 000 r/min±0.5%，瞬态转速调速率为14%。

6 结语

我国电网指标:转速波动率不超过0.5%;负荷波动时，稳定时间不超过5 s，瞬态调速率不超过7%;机组甩负荷时，稳定时间不超过25 s，瞬态调速率不超过20%。

参照电网指标，在既定控制策略下，通过仿真模型模拟燃气轮机发电时动态特性。

当电网负荷波动±4 MW时，稳定时间近乎5 s，因此电网负荷波动不宜超过4 MW。机组甩负荷时，稳定时间为22.99 s，瞬态调速率为14%。

本文的动态特性是基于仿真计算得出，通过与LM2500发电机组甩负荷实测数据比较可看出，计算结果趋势与实测情况基本一致，可认为文中采用的性能仿真方法具有一定参考价值，但仍需在条件成熟时结合实际机组运行情况对研究方法进行修正。

［1］KINGSLE Y J，STAUFFER M. United States Navy Integrated Power System Testing Experience with a LM 2500 Generator Set Utilizing a MicroNet Controloller［A］.2000，ASME IGTI Conference.

［2］HARVAY E，KINGSLEY J.United States Navy Integrated Power System Gas Turbine Generator set test experience［A］.2002 ASME.

Research on transient simulation of gas turbine generator set

LUAN Yong-jun，SUN Peng，LI Dong-ming，YU Shi-kang，DONG Bin
(The 703 Research Institute of CSIC，Harbin 150078，China)

A simulation model was carried on with Matlab/Simulink software for gas turbine generator set performance analysis.Transient gas turbine behavior is calculated for electrical load acceptance and rejection by using this model.Base on electric power system standard and control scheme，an optimization result can be achieved.

gas turbine;generate electricity;simulation

U664.131

A

1672－7649(2012)04－0051－06

10.3404/j.issn.1672－7649.2012.04.011

2011－03－28;

2011－04－25

栾永军(1983－)，男，工学硕士，工程师，研究方向为燃气轮机控制及仿真等。