含间隙碰撞振动系统的非线性振动特性

卢绪祥， 刘正强， 黄树红， 李录平

（1.华中科技大学 能源与动力工程学院，武汉430074；2.长沙理工大学 能源与动力工程学院，长沙410114）

现代机械结构系统中内部或边界上的间隙使在外界激励作用下不同零部件间产生碰撞振动，从而对系统的动力特性、可靠性和寿命等技术指标产生重要影响，如航天器伸展机构和涡轮机械转子系统等机械系统中的运动副间隙引起的碰撞振动导致系统效率和工作精度降低［1］.然而，碰撞（冲击）阻尼器和透平机械叶片的碰撞减振结构却可以利用零部件的相互碰撞来快速传递和耗散能量，从而提高该类结构系统的可靠性和寿命［2－5］.同时，含间隙的碰撞振动系统具有复杂的非线性和不连续性，因此对其进行研究既具有工程实际意义又有较大的理论价值.

一般，含间隙和碰撞的机械振动系统为多参数高维系统，并且碰撞或冲击等因素造成的非线性与奇异性使系统具有很强的非线性动力特性.目前，许多研究者借助非线性振动理论的数值解法获得了该类系统的非线性振动规律：不仅存在着多种周期运动，而且随着参数的变化出现各种分岔（周期倍化分岔、Hopf分岔等），进而演变成概周期、非周期或混沌运动［6－9］.但在研究中全面考虑碰撞中的所有物理过程十分困难，因此需对碰撞条件和碰撞过程进行合理简化，从而建立起比较符合实际的碰撞模型.笔者采用广义Hertz接触理论将该碰撞振动系统等效为无质量弹簧－阻尼器，建立含对称间隙结构的碰撞振动系统动力学模型，然后通过数值求解对该结构模型在不同参数条件下的非线性振动特性进行分析.

1 含间隙碰撞振动系统的动力学模型

含双侧间隙结构的对称碰撞振动系统可简化为如图1所示的动力学模型.将碰撞振子简化为由刚度为k的线性弹簧和阻尼系数为C的阻尼器连接而成的集中质量块m，在简谐激振力Fe＝F0sin wt的作用下发生振动.

当振动位移x大于间隙d或小于间隙－d时，碰撞振子分别与左右两侧质体发生接触碰撞.接触碰撞力用广义Hertz接触碰撞力FR进行描述，因而可以得到其运动方程：

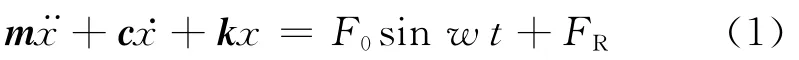
式中：m、c、k分别为碰撞振子的质量矩阵、阻尼矩阵以及刚度矩阵；F0为外界激振力幅值；w为激励圆频率.

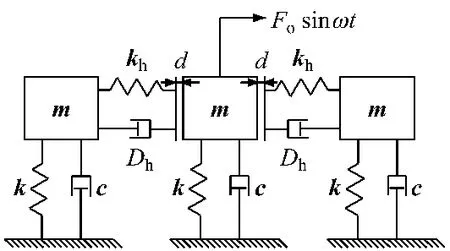
图1 含双侧间隙结构的碰撞振动模型Fig.1 Dynamic model of the impact－vibration system with double－side clearance

为研究碰撞过程中碰撞力的变化，大多学者采用考虑变形的等效弹簧阻尼模型，用弹簧来模拟碰撞中系统构件的变形，用与之串联的阻尼器来考虑接触过程中碰撞体弹性波的影响并反映出碰撞时能量的损耗特性，其中大多数科研工作者采用Hertz接触模型［10］.广义的Hertz接触碰撞力可表示为：

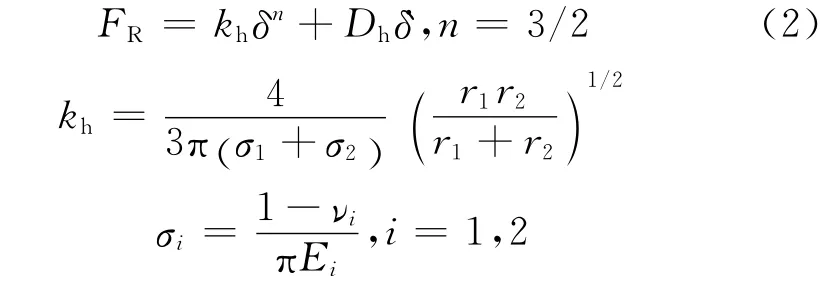
式中：δ为两个质体沿接触面法向相对位移；δ·为相对速度；Dh为阻尼函数，Dh＝λδn；λ为滞后阻尼系数；kh为弹性力学中的Hertz接触刚度，它取决于材料特性和曲率半径；r1和r2分别为两个质体接触点的曲率半径；Ei和νi分别为两个质体的弹性模量和泊松比.

借助于Newton恢复系数e＝－ν／ν0确定碰撞前、后速度，并结合由试验结果拟合的恢复系数对于碳钢和青铜材料，系数ai＝0.08～0.32s／m，一般取一阶近似），再根据碰撞接触过程中的能量守恒可得滞后阻尼系数λ：

故广义Hertz接触碰撞力可表示为：

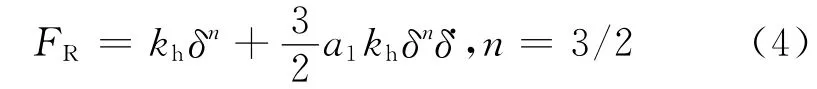
考虑到间隙对动力学模型的影响，故碰撞力可表示为：

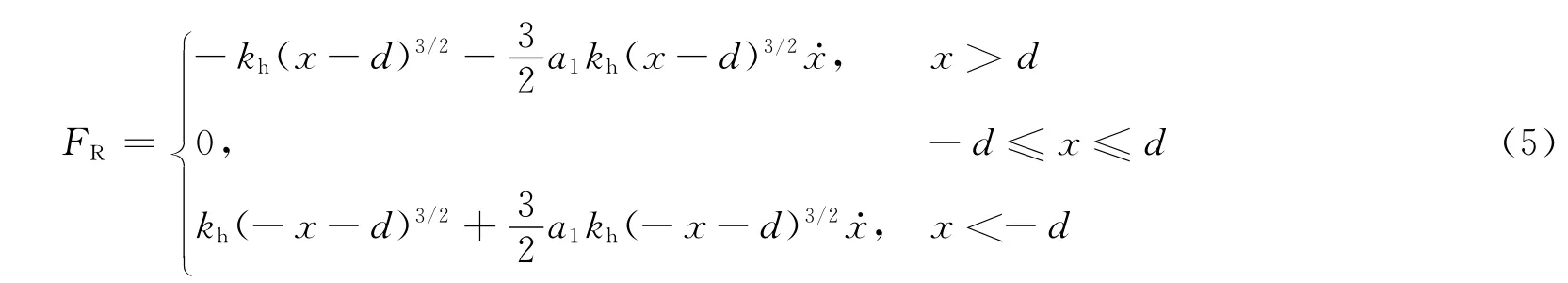
为便于微分方程的数值求解，引入以下参数：无量纲时间τ（τ＝ωnt）、激振力频率ω、固有频率ωn阻尼因子无量纲频率比并引入新变量或新状态量

则可将该动力学模型化成以下状态空间形式：

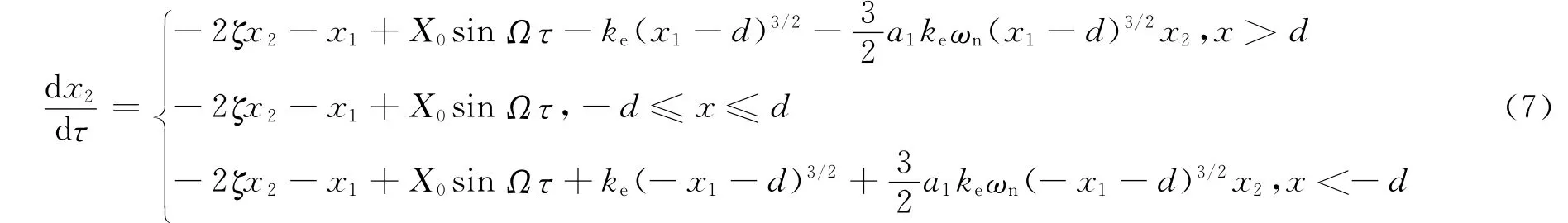
2 数值求解方法与模型相关参数

含间隙碰撞动力学模型中引入了非线性的Hertz接触力，很难直接用解析方法进行求解，因此笔者采用具有良好计算精度和稳定性的四－五阶Runge－Kutta法对该模型的运动微分方程进行数值求解.通过数值仿真得到该含间隙碰撞模型在不同频率比、间隙和激振力幅值下非线性响应的分岔图、时域波形图、相图、Poincaré图和功率谱图，并以此进一步研究该模型的非线性振动特性.

笔者以长沙理工大学振动实验室叶栅碰撞试验台上获得的自带冠叶片参数作为模拟参数进行数值求解.各模拟参数分别为：m＝0.16kg，ζ＝0.02，a1＝0.1，ωn＝2πf1＝421rad／s，kh＝108N／m.在进行频率比变化分析时，其余参数的取值分别为：F0＝20N，d＝0.1mm，Ω＝0.55～1.5；在进行激振力幅值变化分析时，其余参数分别取值如下：d＝0.1mm，Ω＝1.02，F0＝20～50N；在进行间隙变化分析时，其余参数分别取值为：F0＝20N，Ω＝1.02，d＝0～5mm.

3 数值模拟结果与非线性振动特性

3.1 频率比变化对振动特性的影响

图2为在一定激振力幅值F0和间隙d下该模型系统的振动响应振幅x随频率比Ω变化的分岔图.由图2（a）可知：x随频率比Ω 变化经历了周期运动、倍周期运动、拟周期运动以及混沌运动等各种复杂的运动形式，且宽、窄的混沌带随频率比变化交替出现；在频率比约为1时，非线性振动特性变化较为显著.由图2（b）可知：当1＜Ω＜1.031时，系统响应主要以周期运动为主；在Ω＝1.031时，系统响应经过一个倍周期分岔为周期2运动；当1.031＜Ω＜1.034时，进入参数域极窄的混沌运动状态；当频率比Ω达到1.034时，又进入周期2运动；随后在1.048＜Ω＜1.072时，系统响应又进入周期运动，但在Ω达到1.072之后，系统响应由周期运动阵发性进入参数域较宽的混沌运动.

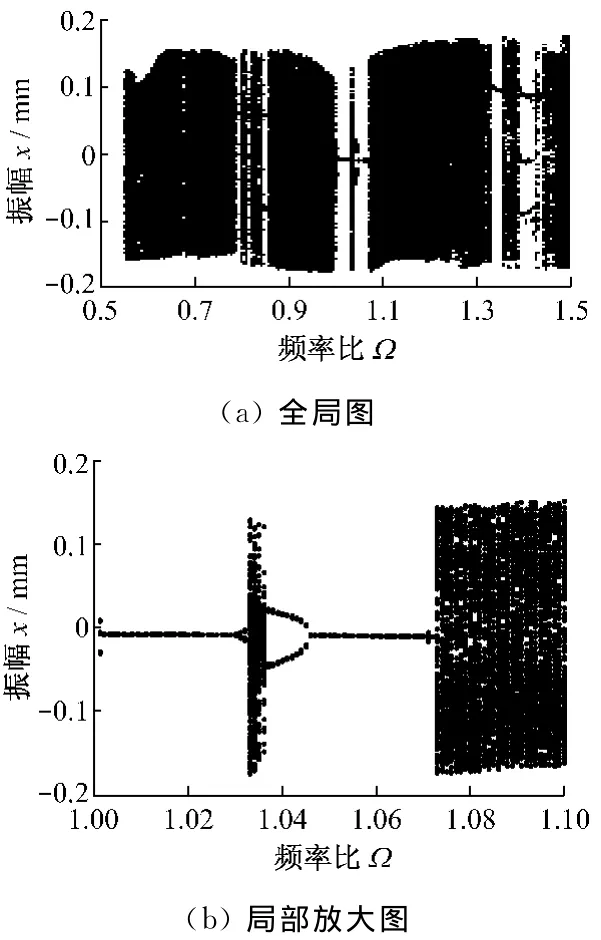
图2 当F0＝20N、d＝0.1mm时模型系统响应振幅x随Ω变化的分岔图Fig.2 Bifurcation diagram of system response xvarying with frequency ratioΩ （F0＝20N，d＝0.1mm）

图3给出了频率比Ω分别为1.02、1.04和1.2时的时域波形图、相平面图、Poincaré截面图和功率谱图.由图3（a）的波形图和相平面图可知：每个周期内碰撞振子在左右两端各碰撞2次；同时，在Poincaré截面图上出现1个孤立点，在功率谱图上只出现了无量纲频率Ω倍频时的孤立谱峰.由此可见，系统在此频率比下呈周期运动状态；当频率比为1.04时，虽然碰撞振子每周期也在左右两端各碰撞2次，但相邻两周期内的碰撞运动情况不同，因此出现了图3（b）中相平面的运动形式，同时在Poincaré截面图上出现2个孤立点，在功率谱图上也出现了除无量纲频率Ω倍频的孤立谱峰以外的分频谱峰，说明系统此时进入了周期2的倍周期运动状态；当频率比为1.2时，从时域图看出系统响应的波形出现了紊乱的峰线，看不出明显的周期波形线，在周期内的碰撞次数变化不定，在相应的相平面图中也呈无规律运动，同时Poincaré截面图呈现分散性堆积的散点图，在功率谱图上出现连续的谱线，说明系统发生了混沌运动.

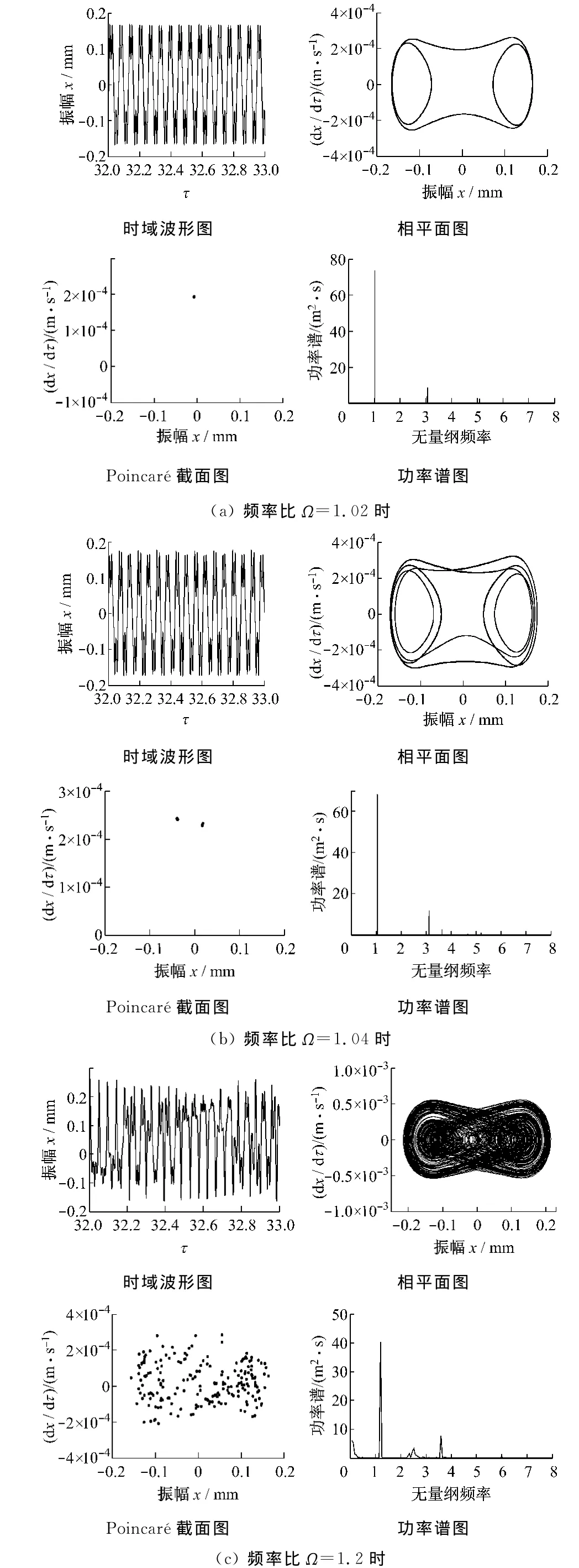
图3 不同频率比时的振动特性Fig.3 Vibration characteristics at various frequency ratios

3.2 激振力幅值变化对振动特性的影响

图4给出了频率比为1.02、间隙为0.1mm时碰撞振动系统响应振幅x随激振力幅值变化的分岔图.由图4可知：在一定条件下，激振力幅值的变化对碰撞振动系统的振动特性有很大影响，在较大的激振力幅值范围内存在着较宽的混沌带，变化范围较长的周期运动和倍周期运动（周期2）只出现在激振力幅值为20～22N、33～35.8N和43～46.7 N内，且其中依然掺杂着混沌运动状态，许多情况下都是由周期运动阵发性进入混沌运动.图5给出了激振力幅值为33.5N和50N时的时域图、相平面图、Poincaré截面图和功率谱图.由图5可知：在激振力幅值为33.5N时出现了周期2的倍周期运动，但碰撞振子在每周期内左右两端碰撞次数各不相同，且在左端的碰撞情况比右端复杂；而在激振力幅值为50N时出现了明显的混沌运动，Poincaré截面图上出现了无规律的散点，且在功率谱图上出现连续的谱线.

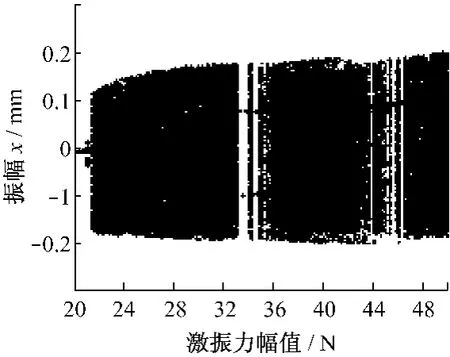
图4 频率比为1.02、间隙为0.1mm时系统响应振幅x随激振力幅值变化的分岔图Fig.4 Bifurcation diagram of system response xvarying with amplitude of exciting force（Ω＝1.02，d＝0.1mm）

3.3 间隙变化对振动特性的影响

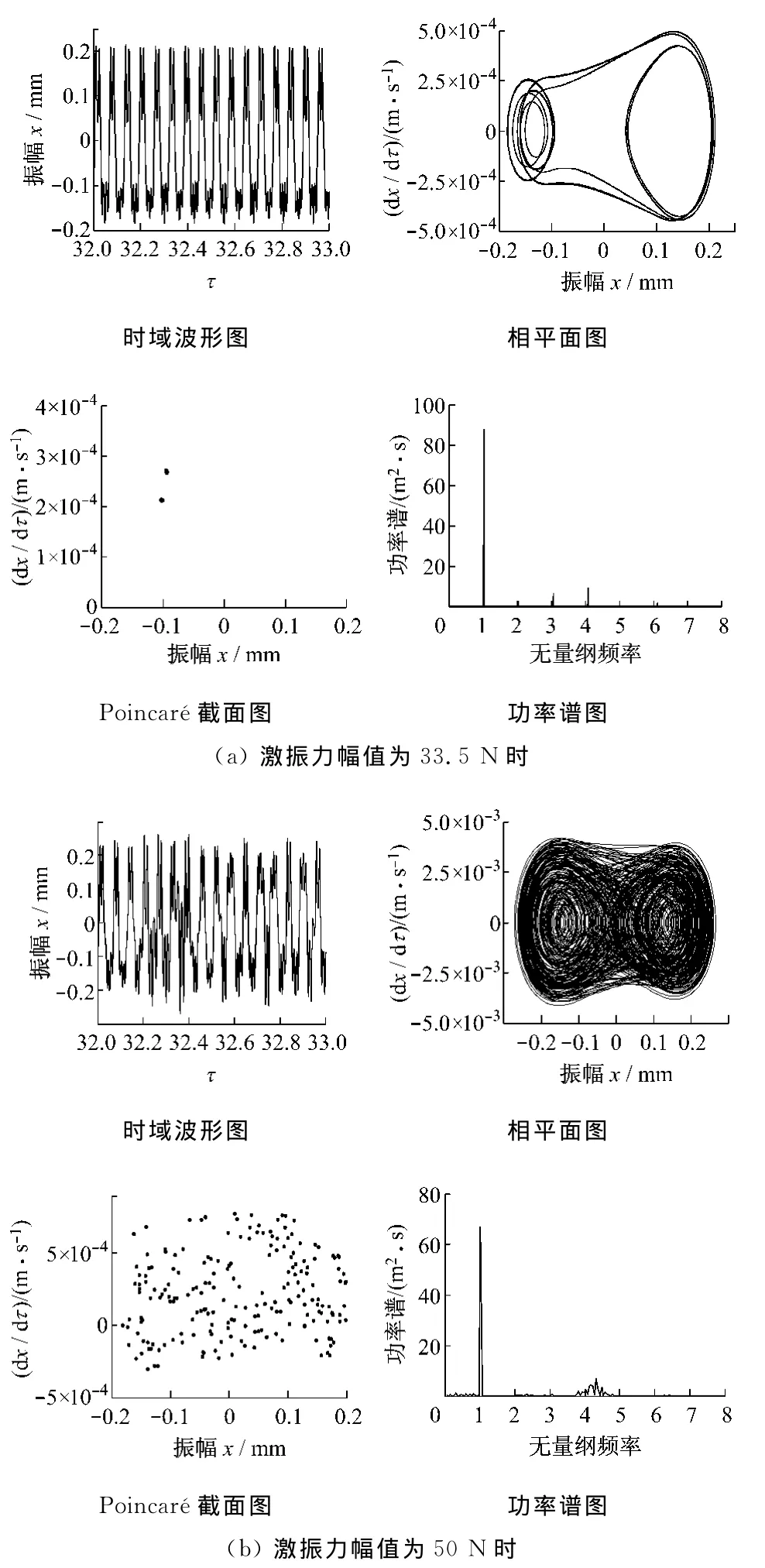
图5 不同激振力幅值下的振动特性Fig.5 Vibration characteristics at various amplitudes of exciting force

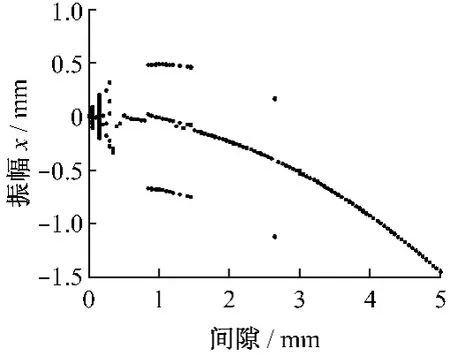
图6 当F0为20N、Ω为1.02时系统响应振幅x随间隙变化的分岔图Fig.6 Bifurcation diagram of system response xvarying with clearance（F0＝20N，Ω＝1.02）

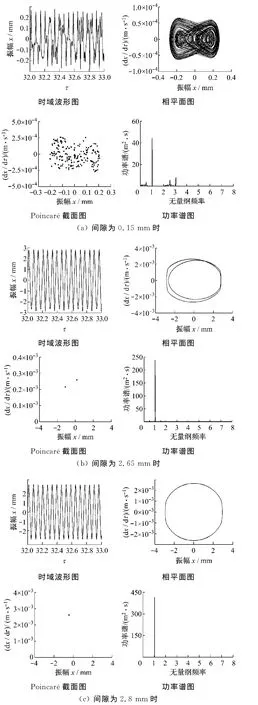
图7 不同间隙下的系统振动特性Fig.7 Vibration characteristics at various clearances

图6为在一定频率比和激振力幅值下系统振动响应振幅x随间隙变化的分岔图.图7为不同间隙下的系统振动特性.由图6可知：当频率比和激振力幅值一定，即外部激振力一定时，间隙变化对系统响应振幅的影响较小，但间隙较小时变化较为复杂，即在间隙d为0～0.4mm时，系统响应振幅出现了周期、倍周期（如间隙为0.2mm时的周期2、0.25mm时的周期3和0.3mm时的周期5运动）和混沌运动；当间隙为0.85～1.45mm时出现了较宽参数域的周期3运动，而在间隙大于1.45mm后，除了在间隙为2.65mm时出现了周期2的倍周期运动外，其余间隙情况下都出现单周期运动，且随着间隙的增大，系统振动响应振幅的幅值也增大.由图7可知，当系统处在不同间隙时，其振动特性不同：当间隙为0.15mm时，碰撞振动系统显现混沌运动，不同周期内碰撞振子在两端的碰撞次数也不同；在间隙为2.65mm时，碰撞振动系统出现周期2运动，碰撞振子在每个周期内都只在一端碰撞1次，功率谱上也出现了1／2分频振动；当间隙增大到2.8 mm或更大的间隙时，系统响应进入了规则的单周期运动，此时在相平面图上呈现椭圆形状，而在功率谱图上则只出现了工频振动的谱峰，说明此时系统已无碰撞.同时，由图7中的各分图还可以看出：碰撞振动系统通过碰撞可以起到良好的碰阻减振作用，且随着间隙的增大，碰撞振动系统的功率增加，这也说明自带冠叶片的冠间间隙大小对其振动特性影响较大，间隙较小时碰撞减振效果较好.

4 结 论

（1）采用广义的Hertz接触理论，将含双侧间隙的谐对称碰撞振动系统的碰撞特性等效为无质量弹簧－阻尼器，建立了一类含对称间隙的碰撞振动动力学模型，可以比较客观地描述该结构的力学特性.

（2）频率比、激振力幅值和间隙对含间隙碰撞振动系统的振动特性均有影响，并随着这些参数的改变，碰撞振动系统出现了周期、倍周期和混沌运动.

（3）频率比和激振力幅值对系统响应的影响很大，出现了较宽的混沌带.而间隙对碰撞振动系统响应的影响相对较小，但在较小的间隙变化范围内，系统的振动特性变化较大.因此，在工程上如要使碰撞振动系统能够处于稳定运动状态，需先研究这些参数在不同情形下的振动特性，以便获得较好的碰撞减振效果，从而提高碰撞振动系统的可靠性.

［1］俞武勇，季林红，阎绍泽，等.含间隙机构运动的动力学模型［J］.机械科学与技术，2001，20（5）：665－670.YU Wuyong，JI Linhong，YAN Shaoze，et al.A survey of dynamics model of pairs with clearances in mechanism ［J］.Mechanical Science and Technology，2001，20（5）：665－670.

［2］陈志坚，吴惠军，叶明，等.复杂非线性隔冲减振系统计算分析［J］.海军工程大学学报，2006，18（4）：34－38.CHEN Zhijian，WU Huijun，YE Ming，et al.A practical method for calculating complexity shock－isolating system with nonlinear stiffness［J］.Journal of Naval University of Engineering，2006，18（4）：34－38.

［3］赵文礼，周晓军.碰撞阻尼器系统的分岔、混沌与控制［J］.振动工程学报，2007，20（2）：161－166.ZHAO Wenli，ZHOU Xiaojun.Bifurcation，chaos and control of vibration systems with impact damper［J］.Journal of Vibration Engineering，2007，20（2）：161－166.

［4］徐大懋，李录平，须根发，等.自带冠叶片碰撞减振研究［J］.电力科学与技术学报，2007，22（1）：1－6.XU Damao，LI Luping，XU Genfa，et al.Research on impact damping of integrally shrouded blades［J］.Journal of Electric Power Science and Technology，2007，22（1）：1－6.

［5］卢绪祥，黄树红，刘正强，等.基于谐波平衡法的带冠叶片接触碰撞减振特性研究［J］.动力工程学报，2010，30（8）：578－583.LU Xuxiang，HUANG Shuhong，LIU Zhengqiang，et al.Study on contact－impact damping characteristics of shrouded blades based on harmonic balance method［J］.Journal of Chinese Society of Power Engineering，2010，30（8）：578－583.

［6］LUO Guanwei. Period－doubling bifurcations and routes to chaos of the vibratory systems contacting stops［J］.Physics Letters A，2004，323（3／4）：210－217.

［7］HAN R P S，LUO A C J，DENG W.Chaotic motion of a horizontal impact pair［J］.Journal of Sound and Vibration，1995，181（2）：231－250.

［8］乐源，谢建华.一类三自由度碰撞振动系统的Poincaré映射的对称性、分岔及混沌［J］.四川大学学报：工程科学版，2008，40（1）：27－31.YUE Yuan，XIE Jianhua.Symmetry bifurcation and chaos of the Poincarémaps in a three－degree－of－freedom vibro－impact system ［J］.Journal of Sichuan University：Engineering Science Edition，2008，40（1）：27－31.

［9］丁旺才，张有强，谢建华.含对称间隙的摩擦振子非线性动力学分析［J］.摩擦学学报，2008，28（2）：155－160.DING Wangcai，ZHANG Youqiang，XIE Jianhua.Analysis of nonlinear dynamics of dry friction oscillators with symmetric clearance［J］.Tribology，2008，28（2）：155－160.

［10］金栋平，胡海岩.碰撞振动与控制［M］.北京：科学出版社，2005.