基于梯度有限元的异质材料实体优化设计

吴振华， 赵 韩， 董玉德， 柳吉庆

（合肥工业大学机械与汽车工程学院，安徽 合肥 230009）

异质材料实体（HO）是指由两种或两种以上材料组成的实体，若材料组分和属性在空间光滑变化则也称为梯度功能材料（FGM），其作为一种新型复合材料在化工、电子、机械、生物医学工程等领域得到日益广泛的应用[1-2]。近年来，随着超声波固结（UC）、激光近净成形（LENS）、直接金属沉积（DMD）等快速成型工艺技术的发展，允许材料组分以区、层、点为单位变化，异质材料实体的制备更具有灵活性和经济性[3-4]。相应的异质材料实体的计算机图形学表示、设计和分析技术也日趋成熟[5]，吴晓军等[6]提出了一种基于CAD零件离散体素模型的异质材料建模方法，寇欣宇等[7]提出了一种基于非流形几何与特征树的异质材料实体可视化方法，Yang等[8]提出了基于 B样条曲线和图形放样的异质材料实体设计和有限元分析流程，Kim等[9]提出了梯度有限元的概念和理论模型，用以表示各向同性或正交异性的非均质梯度功能材料。

对材料的空间分布进行优化则以拓扑优化为代表，主要采用均匀化方法、水平集方法和渐进结构优化方法等[10-11]。Guest等[12]将节点变量引入拓扑优化，但采用邻域映射法将节点解转换为单元解进行后续计算。优化异质材料实体本质上就是确定组成材料在空间中的体积分数的分布。Huang等[13]基于复合材料微观结构分析空间点的有效属性并通过优化微观结构单元的几何尺寸和偏置角度来优化宏观材料的分布。Carbonari等[14]设计了压电梯度材料致动器、分类进行灵敏度分析并运用均匀化方法对材料分布进行优化。本文提出了基于节点变量和梯度有限元的材料优化模型、运用结构优化移动渐近线算法实现异质材料实体功能最优的完整设计流程。

1 梯度有限元方法

建立计算模型首先需要建立复合材料的有效属性与组分材料体积分数的映射关系。异质材料实体的每一个点都是各向同性的复合材料，本文采用Hashin-Shtrikman下边界作为插值模型来拟合由快速成型（RP）技术制备出来的梯度材料的弹性模量[15-16]。拟合的复合材料的有效杨氏模量算式为

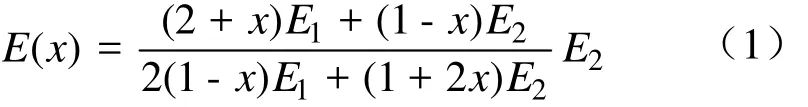
式中， x ∈ [0 ，1]为组分材料的体积分数，E1≥E2分别为两相组分材料的杨氏模量，该公式适用于二维弹性问题。钢、铝复合材料有效杨氏模量的几种插值函数与体积分数变量关系，如图1所示。Voigt边界和Reuss边界适用于每一个点都是各向异性材料的结构体。

以一阶拉格朗日四边形单元（Q4）对二维实体空间划分网格，每个节点处的体积分数向量作为优化变量，即 x =[x1， …，xnn]，式中nn为网格总节点数。其函数在空间 C0连续，单元内的体积分数分布由双线性插值决定，保证了函数的协调性和连续性，这种有限元即称为梯度有限元。节点处的杨氏模量ki由节点处的体积分数xi代入式（1）进行计算，则网格第e个单元内的杨氏模量分布函数为

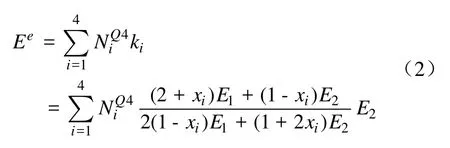
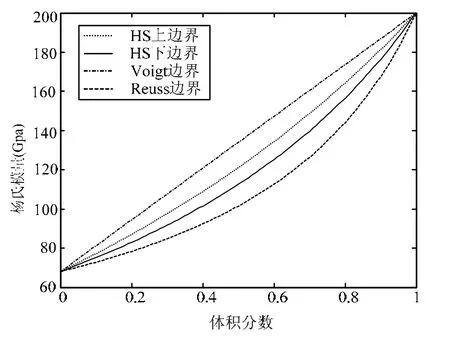
图1 钢、铝复合材料有效杨氏模量的拟合曲线

式中，ν即泊松比，将式（2）代入即可求解。平面应力问题的梯度有限元的总体刚度矩阵为

式中，ne为网格总单元数， Le为第e个单元的离散关系矩阵， Ke为第e个单元的刚度矩阵，Be为形函数第e个单元的空间偏导数矩阵，将式（3）代入即可求解。此时，根据Ku=f可求解有限元模型得出位移向量u并进行后处理。

拓扑优化通常采用单元变量进行分析和优化，即每个单元内材料是均质的。图2比较了基于单元变量的均质四边形单元(a)和基于节点体积分数变量的梯度四边形单元(b)的可视化效果。

图2 均质单元和梯度单元的可视化

2 材料分布优化模型

材料分布的优化问题可抽象为以下数学模型

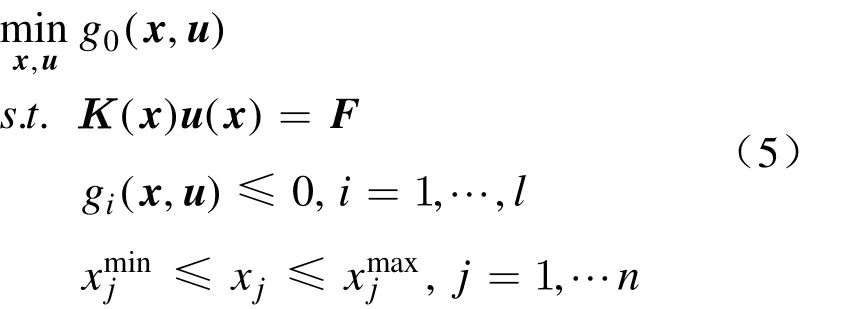
本文求解计算基于节点变量、梯度单元的有限元模型，上述优化问题以及设计异质材料实体的过程如图3所示。

2.1 灵敏度分析

移动渐近线算法是一阶方法，需要目标函数和约束函数的一阶偏导数即灵敏度。本文用解析方法求解灵敏度。由式（1）计算得复合材料有效杨氏模量函数对节点变量体积分数xj的灵敏度为

①北京市委组织部把生态清洁小流域建设、农村治污达标率作为各区县委、政府领导班子届中考核的指标，明确了地方政府责任。政府出台《关于推进山区小流域综合治理和关停废弃矿山生态修复的意见》（京政办发〔2006〕66 号），市发改委、市财政局每年从基本建设资金、水资源费和土地出让金中安排一定比例资金用于生态清洁小流域建设；投资标准从25万元/km2提高到 50万元/km2；制定废弃矿山治理规划，实现全市现有3 667 hm2废弃矿山全部生态修复，裸露矿山重新披绿；2014年标准又提高到 65万元/km2。

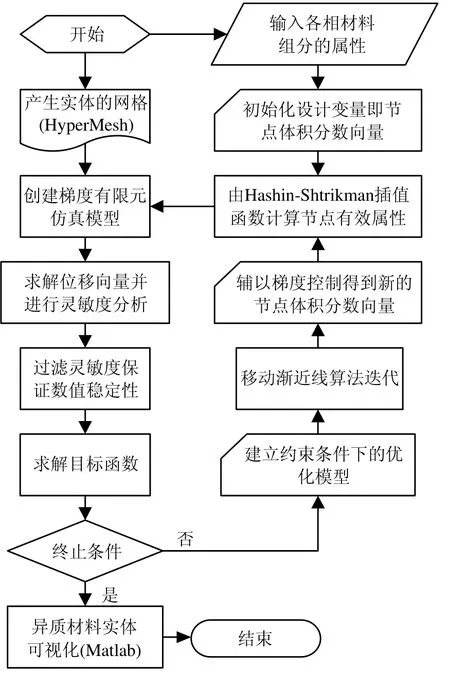
图3 异质材料实体设计优化流程图

由式（4）计算得有限元模型总体刚度矩阵对节点变量体积分数xj的灵敏度为

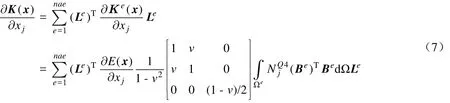
式中，nae为包含全局第j个节点的单元数，将式（6）代入即可求解。对平衡方程K(x)u(x ) =F求偏导数得

式中，k为优化迭代次序号，此式具有平衡方程的形式，右边项视为假载[17]（pseudo-load），将式（7）代入并使用求解有限元模型的同一求解器即可解得

由二维Q4单元划分网格的异质材料实体的重量写作

式中， Ae为第e个单元的面积，t为厚度。由此可计算重量对节点变量体积分数xj的灵敏度为

2.2 移动渐近线算法

Svanberg[18]提出移动渐近线（MMA）算法后该算法因能适应结构优化问题的特性而得到广泛应用，其在广义结构优化问题上近似精确度高于序列线性规划（SLP），运算量低于序列二次规划（SQP），收敛速度快于凸线性化方法（CONLIN）[10]。本文基于梯度单元节点变量的异质材料分布优化问题设计变量数目庞大，适于以MMA算法进行优化。

移动渐近线算法引入如下中间变量

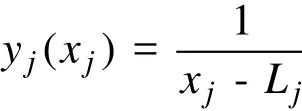
式中Lj及Uj即所谓的移动渐近线，随着迭代而变化，且对第k次迭代来说始终满足算法对目标函数和约束函数gi,i = 0,… ,l 在第k次迭代的迭代解 xk处的近似为

式中， r ik为残值，且有

则优化问题（5）在第k次迭代处的移动渐近线近似可写作

式中， μ ∈ (0,1)，则原优化问题（5）在第k次迭代处被近似为一个具有显式、可分特性的简单的凸优化问题（14），利用拉格朗日对偶可得出在第k次迭代处的最优解并代入下一次迭代，直至满足优化终止条件。

3 梯度控制算法

在异质材料实体设计方法中，材料的体积分数和物理属性通过Q4单元的双线性形函数实现了在二维设计空间中的0C 连续，避免了材料空间分布突变造成应力集中[1]，为了提高该设计优化方法的鲁棒性和自主性，有必要使设计者可以直接控制异质材料在空间中的梯度大小。Petersson等[19]将基于均质单元和单元变量的邻域单元梯度约束引入拓扑优化，提供了一种直接控制局部材料梯度的方法，并且因此减少了数值计算中的棋盘模式和网格依赖现象，但这种算法大大增加了运算量。本文将该局部材料梯度控制方法应用于梯度单元和节点变量，并演化成一种新算法提高计算性能。

图4为梯度控制算法的网格示意图，Ωi为节点i的邻域，邻域半径为r，d(i,j)为节点i与节点 j的距离， Ωij∈ ，梯度约束可表示为

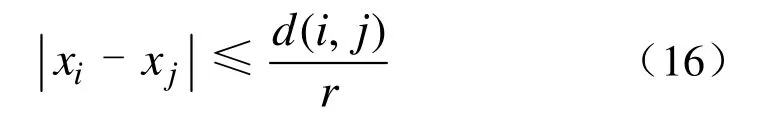
图4 节点邻域梯度控制示意图

式中，xi和xj分别为节点i和节点 j处的设计变量， 此式引入了个线性约束函数，直接计算不具备经济性，因此提出实施如下设计变量自适应下界来实现式（16）的约束

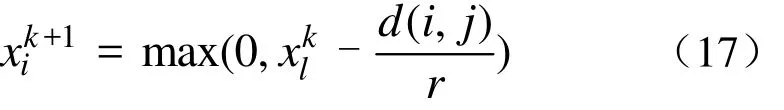
4 优化设计实例

本文以金属夹钳为例来验证说明前述的异质材料实体设计优化方法。以钢、铝为两相组成材料设计如图5所示的夹钳，设厚度t=1mm。设定钢和铝的杨氏模量分别为200GPa和68GPa，密度分别为7.85g/cm3和2.64g/cm3，两者泊松比差别细微，简便起见均设为 0.3。将该夹钳划分为Q4单元的网格，以重量为目标函数，A节点和B节点的Y方向位移为约束函数建立优化数学模型如下

式中，W为夹钳重量，uyA和uyB分别为A点和B点的Y方向位移，x为设计变量，设为各节点处钢的体积分数向量，初始化为，按前文所述方法进行灵敏度分析、移动渐近线优化，得到的最优材料分布如图6(a)所示，与图6(b)所示的由商业软件 Optistruct计算得到的相同结构的载荷路径拓扑图相比，可看到强度较高的钢的分布与载荷路径拓扑有异曲同工之处。

图5 夹钳的尺寸及载荷工况

图6 夹钳的梯度材料最优分布与载荷路径对比

表1对比了不同材料组成的夹钳在载荷工况下的重量和位移，钢、铝最优分布的异质材料夹钳在满足位移约束的前提下重量达到了极值，而位移值又比同样材料比例组成的均质合金的位移值要小。

表1 不同材料金属夹钳重量和位移对比

5 结 论

本文在简明的梯度有限元概念基础上提出的启发式异质材料实体设计优化方法，流程清晰，运算量合理，可以在二维空间得出实体材料的最优分布，从而使设计目标和设计约束达到最优的均衡。这种设计方法避免了基于单元变量的材料分布优化所导致的材料突变，具有材料梯度可控且控制方法运算量小的特点。因为利用了有限元自身的形函数对材料分布进行空间插值从而使得计算过程大大简化，并且同时达到了材料分布的C0连续。这种设计方法可以向三维空间扩展并广泛应用到梯度功能材料的分布设计中去。该方法的缺点是只能设计两相材料实体，如何处理两相以上的材料的分布优化成为了下一步工作的重点。

[1] Miyamoto Y. Functionally graded materials: design,processing,and applications [M]. Chapman & Hall,1999: 1-27.

[2] Pompe W,Worch H,Epple M,et al. Functionally graded materials for biomedical applications [J].Materials Science and Engineering A,2003,362(1-2):40-60.

[3] Hu Yuna,Blouin V,Fadel G M. Design for manufacturing of 3D heterogeneous objects with processing time consideration [J]. Journal of Mechanical Design,2008,130(3): 371-379.

[4] Zhan Y B,Lin D J,An Q. Slicing method for reverse engineering based on image mosaic [J]. Computer Aided Drafting,Design and Manufacturing,2008,(02):33-38.

[5] Hung SKFC,Deng Z M. Thermal design and optimization of heat pipe radiator for satellites [J].Computer Aided Drafting,Design and Manufacturing,2010,(01): 56-64.

[6] 吴晓军,刘伟军,王天然. 三维 CAD零件异质材料建模方法[J]. 机械工程学报,2004,40(5): 111-117.

[7] 寇欣宇,王以忠,彭一准. 基于非流形几何与特征树的异质材料实体可视化方法[J]. 计算机辅助设计与图形学学报,2008,20(4): 532-539.

[8] Yang Pinghai,Qian Xiaoping. A B-spline-based approach to heterogeneous objects design and analysis [J]. Computer-Aided Design,2007,39(2):95-111.

[9] Kim J H,Paulino G H. Isoparametric graded finite elements for nonhomogeneous isotropic and orthotropic materials [J]. Journal of Applied Mechanics,2002,69(4): 502-514.

[10] Bendsøe M P,Sigmund O. Topology optimization:theory,methods,and applications [M]. Berlin:Springer Verlag,2003: 10-30.

[11] Rozvany G. A critical review of established methods of structural topology optimization [J]. Structural and Multidisciplinary Optimization, 2009, 37(3):217-237.

[12] Guest J K,Prévost J H,Belytschko T. Achieving minimum length scale in topology optimization using nodal design variables and projection functions [J].International Journal for Numerical Methods in Engineering,2004,61(2): 238-254.

[13] Huang Jinhua,Fadel G M,Blouin V Y,et al.Bi-objective optimization design of functionally gradient materials [J]. Materials & Design,2002,23(7): 657-666.

[14] Carbonari R C,Silva E,Paulino G H,et al. Topology optimization design of functionally graded bimorph-type piezoelectric actuators [J]. Smart Materials and Structures,2007,16: 2605-2620.

[15] Walpole L J. On bounds for the overall elastic moduli of inhomogeneous systems—I [J]. Journal of the Mechanics and Physics of Solids,1966,14(3):151-162.

[16] Bendsøe M P,Sigmund O. Material interpolation schemes in topology optimization [J]. Archive of Applied Mechanics (Ingenieur Archiv),1999,69(9):635-654.

[17] Christensen P W,Klarbring A. An introduction to structural optimization[M]. Springer Verlag,2008:93-99.

[18] Svanberg K. The method of moving asymptotes: a new method for structural optimization [J].International Journal for Numerical Methods in Engineering,1987,24(2): 359-373.

[19] Petersson J,Sigmund O. Slope constrained topology optimization [J]. International Journal for Numerical Methods in Engineering,1998,41(8): 1417-1434.