基于弧长参数化的曲面W-M分形插值

刘远东， 王清辉， 刘 林， 熊 巍

（1. 华南理工大学设计学院，广东 广州 510006；2. 华南理工大学机械与汽车工程学院，广东 广州 510640）

有研究表明，机械加工表面的微观粗糙形貌具有统计意义上的自仿射分形特性[1]，对机加表面可以像描述自然界的非规则结构一样，使用分形几何对表面微观形貌进行表征建模。假设机加工表面微观轮廓具有连续性，尽管这个假设在原子尺度时是不成立的，但对于机加工表面而言，一直到零长度尺度的极限情况，连续性假设都是成立的。据观察，如果表面微观轮廓被重复放大时，更加精细的结构会不断出现，而且轮廓永远是不光滑的，在任何点均不存在切线，所以轮廓是处处不可微性。另外，当轮廓被放大时，放大后的表面和原始表面的概率分布非常相似，因此大多数轮廓具有自仿射性。Mandelbrot于1982年在Weierstrass函数基础上提出了一种分形曲线的函数表达形式，称为Weierstrass- Mandelbrot函数（简称W-M分形）。分形几何学中的W-M函数满足连续性、处处不可微、自仿射性这些数学特征，因此Majumdar A用它来表征机械加工表面的微观轮廓[2]。

Chen[3]等利用W-M分形模型和理论分析了微流道的层流表面，指出微流道的表面微观形貌可以利用分形几何的方法予以描述，而且自仿射的分形维数反映了表面粗糙形貌的微观特征，自仿射分形维数越大，表面结构变化就越大，从而压力损失也越大。Bobji[4]等利用用W-M分形理论建立了岩石表面结构的三维仿真模型，研究了分形维数D和均方根rms对岩石硬度的影响，从而利用W-M分形理论来进行岩石硬度的测量。李成贵[5]等指出工程表面的几何特征与零件的摩擦、磨损、接触、润滑、磨削机理、金属结构等机械或物理性能有着密切的联系，通过计算W-M三维分形表面形貌的分形维数，并进行精密加工试件实验，研究了各种分形维数与工程表面的形貌、加工参数、机械性能等的关系。He[6]等利用分形理论，对摩擦的合金表面进行取样，通过分形参数D和G的分析，从而研究合金表面摩擦特性。吕建国[7]等研究了不同分形维数Ds的W-M分形曲面多重分形谱的变化规律，用分形参数定量表征分形曲面的分布特征，并指出多重分形谱很好地表征了W-M分形曲面的高度分布规律。张毅[8]将分形理论应用在扫描隧道显微镜测量的一组微镜的表面形貌的分析中，指出W-M 函数可用于微镜表面的建模和形貌分析。

然而，以上研究的都是基于直线上或平面上的W-M分形，在众多的工程应用中，机械表面的微观形貌往往是叠加在自由曲线或曲面上的。因此，对这些机械表面微观形貌不能直接采用W-M分形进行模拟，而需要研究将W-M分形与自由曲线曲面合成的有效计算方法。本文针对具有自由曲面形状的机械加工表面微观形貌建模，研究将弧长参数化引入参数曲面上的W-M分形插值的计算方法。

1 W-M分形模拟

1.1 W-M二维曲线模拟

分形几何学中W-M函数的数学表达式为[9]

式中，x表示轮廓的位置坐标，D为分形维数，它描述函数z(x)在所有尺度上的不规则性，但不能确定z(x)的具体尺寸；G是特征尺度系数，反映 z(x)幅值大小，它决定 z(x)的具体尺寸；γn表示轮廓的空间频率，γ为大于1的常数，对于服从正态分布的随机轮廓，γ=1.5可适用于高频谱密度及相位的随机性，由于粗糙度轮廓是非稳定的随机过程，轮廓结构的最低频率与粗糙度样本长度关系为 γn1≈1/L1；n1是W-M函数的初始项，为整数；L1为粗糙度样本取样长度。

图1是基于上述W-M分形公式得到的一段分形曲线轮廓。

图1 W-M二维分形插值曲线

1.2 W-M三维曲面模拟

W-M 函数实际上是空间不同层次不同频率的正弦/余弦曲线叠加而成，其中一种常用的产生随机分形表面的典型函数由式（2）表示[10]

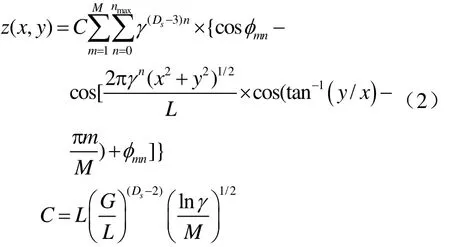
其中，C是表面的高度系数，Ds是空间分形维数且有 Ds=D+1，D是截面的分形维数，Φ是一系列0到π之间的随机相位，γ是控制表面起伏密度的参量，M是空间起伏的数量，L为拟图像的大小，G则是调整粗糙度的一个系数。对于一个完全分形的表面，有nmax→∞ 。图2是在Object ARX环境下运用W-M三维模拟公式得到的一张分形插值曲面模型。

图2 W-M三维分形插值曲面

2 弧长参数化

2.1 弧长参数化的定义

弧长参数化是指基于曲线自身的累积弧长建立参数方程。在许多实际问题中，需要对曲线进行弧长参数化。例如，数控加工中要求实现刀具运动轨迹的弧长到空间位置的“时空”转换，这里要求弧长作参数，这样只要给出弧长即可立刻计算刀具的位置。

以 sin(t)曲线的弧长参数化为例，插值时以均匀递增的累积弧长作为W-M分形插值的参数变量，可得到W-M分形曲线与sin(t)曲线叠加的分形模型。图3是利用弧长参数化得到的 sin(t)曲线上的W-M分形曲线例子。

图3 sin(t)曲线上的W-M分形曲线

2.2 弧长参数化必要性

对参数方程为P(t)的曲线进行W-M分形插值时，如果直接以均匀递增的参数 t作为 W-M分形插值的参数变量，必然导致W-M分形插值沿曲线表面分布的不均匀。在曲线参数密度大的地方，分形插值点会相对密集；在参数密度小的地方，W-M分形插值点相对稀疏。

图4(a)是直接基于曲线参数变量驱动得到的一条NURBS曲线上的W-M分形插值曲线，该曲线左边参数密度大处，W-M分形插值点密集；而曲线右边参数密度较小，造成W-M分形插值分布稀疏。图4(b)是采用弧长参数作为驱动变量得到的NURBS曲线上的W-M分形插值曲线，插值点是均匀的，它不随曲线的参数密度变化而变化。由于机械表面的微尺度形貌特征是独立与其宏观几何形状而存在的，而更多地受到表面微分几何特征的影响，因此，采用弧长参数作为驱动变量对于实现参数曲线上的W-M分形插值是必要的。

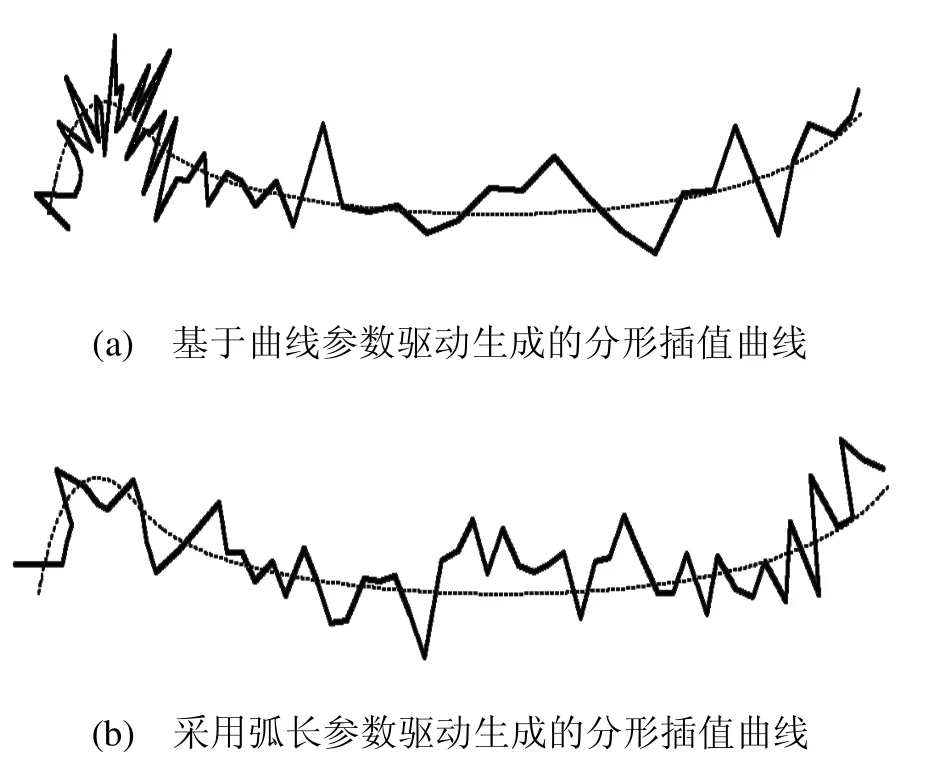
图4 两种参数驱动生成的W-M分形插值曲线对比

3 曲面W-M分形模拟

3.1 弧长参数化的实现

本文以AutoCAD环境下的一张NURBS拉伸曲面为例，说明弧长参数化的实现方法。假设，W-M分形插值模拟分辨率为m_nCol×m_nRow个插值点，且曲线的拉伸方向插值点个数为m_nCol，弧长参数化方法如下：

步骤1将曲线的参数区间(ts，te)分为n等份（n=m_nRow×Pric，Pric为设定的弧长参数化精度），利用微分法求出每一ti(i=0,1,…,n-1)所对应累积弧长si，故曲线总弧长为sn-1。

步骤2反求出m_nRow个等弧长点ks～对应的参数tk，其中m_nRow-1。让ks ～在弧长区间 ( s0,sn-1)内由s0开始搜索，若判得，则认为si≈ks ～，保存此时的参数值tk。由于本插值问题不同于一般的弧长参数化，对每一个进行搜索时，不必均从s0开始搜索，因为弧长S(t)是单调递增函数，所以，若上一次迭代得(k-1)对应的值为sj，那么ks ～在区间(sj,sn)从sj开始搜索，这将大大减少弧长参数化的算法实现时间。

步骤3前面已求得等递增的累积弧长对应的参数值tk，由Object ARX的求值函数可求出tk对应的坐标Pk和曲线法向量Vk，再求出W-M分形插值的高度值Hk，根据Pk、Vk和Hk可求出最后的W-M分形插值点。对于二维W-M分形插值，把ks ～作为x值代入式(1)求Hk；对于三维W-M分形插值，若拉伸曲面沿y方向拉伸，则y方向的值不变，ks ～代替x，代入式(2)求Hk。

3.2 W-M分形模拟对比

对于曲线上的二维 W-M 分形插值模拟对比，图4给出了模拟结果，其中插值点个数为40。对于曲面上的三维 W-M 分形插值，图 5(a)是一张NURBS拉伸曲面，图5(b)显示了直接以曲面参数进行插值得到的分形曲面，而图5(c)则是以弧长参数化方式得到的分形插值曲面，其中插值分辨率均为45×15。从图形对比可以观察到，采用弧长参数驱动生成的分形插值曲面其分形形貌分布均匀。

图5 两种参数驱动生成的W-M分形插值曲面对比

4 两向异性的W-M分形

在对上述表面微观形貌进行模拟时，我们假设其微观形貌特征的分布是各向同性的。但事实上，很多机械加工过程产生的表面其微观形貌特征呈很强的方向性[11]。工程一般认为，各向异性表面的加工纹理，就是加工痕迹的线条方向。纹理的种类有平行、垂直、相交、微粒状、圆形、放射状[12]。这里我们先以沿x方向和y方向的两向异性情况为例研究其数学模型的表示。

本文提出以x方向的二维W-M分形和y方向的二维W-M分形相叠加的方法来实现这种两向异性的W-M分形模拟，公式如下

其中，Gx和Dx为沿x方向的分形比例系数和分形维数；Gy和Dy为y方向的分形比例系数和分形维数。

由式(3)可知，当x或y为一定值时，z(x,y)演变为二维W-M分形轮廓线。这也表明，利用该式模拟的曲面，在x方向或y方向上的任意轮廓线均具有分形特征。

图6(a,b)分别是由式(3)进行W-M插值得到曲面，两插值曲面的尺度范围不同，其中图6(a)为 100×100，图 6(b)为 10×10。从图中可看出，曲面的x方向和y方向是异性的，且两曲面具有自相似性。图 6(c)表明当 Gx和 Gy相等、Dx和Dy相等时，插值曲面在x和y两方向同性。图6(d,e)则显示在 Gx、Gy相等的情况下，由于 Dx和 Dy不同得到x方向和y方向两向异性的分形曲面。

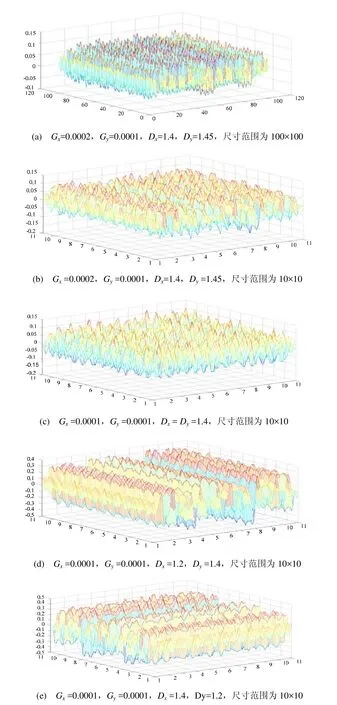
图6 两向异性W-M分形模拟曲面

通过前面提出的弧长参数化方法以及各向异性W-M分形插值公式，可以在参数曲面上合成具有的各向异性W-M分形插值曲面。图7展示了两张在NURBS拉伸曲面上合成的各向异性W-M分形曲面。

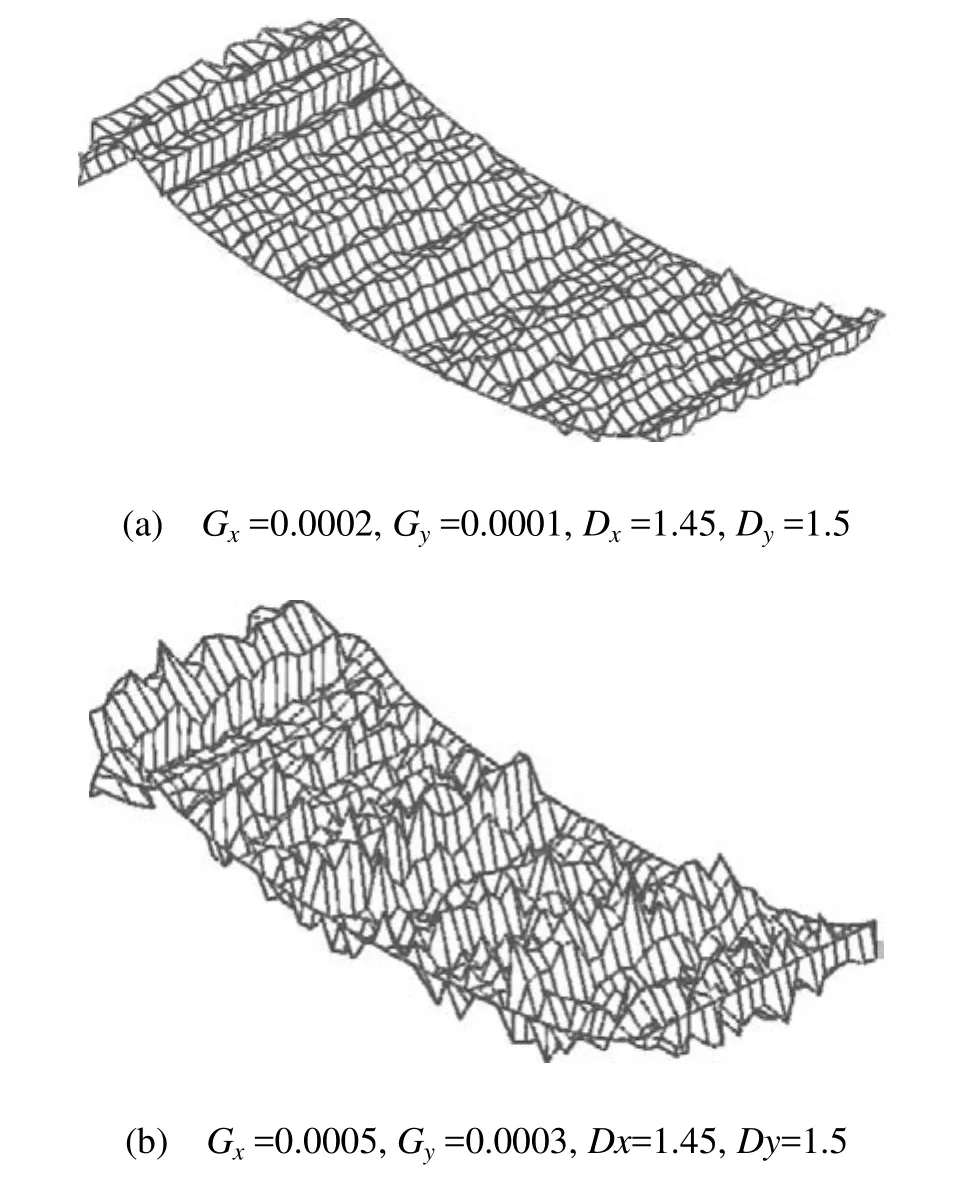
图7 曲面的两向异性W-M分形模拟曲面

5 结 论

本文论述了在参数曲面上合成W-M分形在机械加工表面微观形貌建模中的意义，指出了弧长参数化在该建模过程中的必要性，并提出了具体实现方法。通过该方法，利用 AutoCAD ObjectARX开发包实现了曲线和曲面的W-M分形插值模拟。在此基础上,提出了一种两向异性W-M 分形曲面的数学建模方法，实现了在参数曲面生成两向异性W-M分形插值模拟。

[1] 董 霖,王 艳,王 霜. 机械加工表面分形特征的数学表征[J]. 机械,2001,28: 52-53.

[2] Majumdar A,Tien C. Fractal characterization and simulation of rough surfaces [J]. Wear,1990,136:313-327.

[3] Chen Y P,Zhang C B,et al. Role of surface roughness characterized by fractal geometry on laminar flow in microchannels [J]. Physical Review,2009,80(026301):1-7.

[4] Bobji M S,Shivakumar K,et al. Influence of surface roughness on the scatter in hardness measurements-a numerical study [J]. International Journal of Rock Mechanics and Mining Sciences,1999,36: 399-404.

[5] 李成贵,董 申. 三维表面形貌的分形维数计算方法[J]. 航空精密制造技术,2000,(8):36-40.

[6] He L,Zhu J. The fractal character of processed metal surfaces [J]. Wear,1996,208(197): 17-14.

[7] 吕建国,戴结林,宋学萍. Weierstrass-Mandelbrot分形曲面的多重分形谱[J]. 功能材料,2008,(9):1574-1576.

[8] 张 毅,罗 元,徐晓东. 基于分形理论的 MEMS光开关微镜分析与模拟[J]. 半导体光电,2006,(6):672-674.

[9] Majumdar A,Bhushan B. Fratal model of elasticplastic contact between rough surfaces [J]. Journal of Tribology,1991,113: 1-13.

[10] Yan W,Komvopoulos K. Contact analysis of elastic-plastic fractal surfaces [J]. Journal of Applied Physics,1998,84(7): 3617-3624.

[11] 喻志清,戴泽西,陈志祥. 外圆磨削表面轮廓的分形行为研究[J]. 华中理工大学学报,1998,(3):49-50.

[12] Thomas T R,Rosen B G,Amini N. Fractal characterization of the anisotropy of rough surfaces [J]. Wear,1999,232: 41-50.