基于蚁群改进BP算法的组合预测模型

李 连，孙 聪，苏 涛

(海军航空工程学院 a.控制工程系;b.研究生管理大队，山东 烟台 264001)

随着计算机科学与技术的发展以及社会经济系统的日益复杂，众多学者探索了各种预测技术。发展至今，实际应用中较常使用的预测方法已有几十余种。每种预测方法都具有自身的特点，都是对系统内部某方面特征的刻画，揭示了部分的变动规律，因此不能单纯绝对的评价某种方法的优劣，比如神经网络对于复杂因素具有很强拟合能力，但是对于不同结构的数据样本，预测差异性较大，稳定性不足;灰色预测有较强的趋势项模拟能力，但当序列数据变化急剧时往往会产生较大误差;ARMA 时序模型用于非平稳数据建模能够较好地处理随即扰动因素。为了综合利用各项预测方法的优势，Bates 和Granger 建议使用组合预测方法来综合反映系统内部全部信息，从而提高预测精度和效率［1］。在组合预测的研究中已经证实非线性组合预测比线性组合预测的精度要高，但是非线性组合预测中的非线性函数形式的选择和参数估计等问题始终是困扰建模者开展预测工作的关键所在。本文提出基于蚁群算法优化BP 神经网络的组合预测模型，首先用灰色预测和ARMA 时序预测利用历史数据进行预测，将其结果作为改进BP 网络的输入，从而构建组合预测模型，并将其最终结果与其他预测方法进行对比。

1 单项预测模型

1.1 灰色预测模型

灰色系统理论主要是通过对“部分”已知信息的提取、分析，得到较为有价值的信息，从而实现对系统行为趋势进行较正确地描述和较有效地控制。灰色系统理论分析问题的主要思想是:尽可能有效、积极地发挥系统已知信息和规律，尽可能准确地提取灰色信息中有效信息，尽可能成功地规避被分析系统中的黑色信息，其过程就是将灰色系统从知之较少到知之较多转变［2］。

GM(1，1)模型法是该理论中的重要方法之一。建立GM(1，1)模型的实质就是对原始序列进行1次累加，使生成的序列呈现一定规律，然后建立一阶线性微分方程模型，求得拟合曲线来对系统进行预测。GM(1，1)模型是最常用的一种灰色模型，是由一个只包含单变量的一阶微分方程构成的模型。建立GM(1，1)模型的方法是［3-5］:

1)累加生成:设数据样本的时间序列X(0)有n 个样本值，X(0)={X(0)(1)，X(0)(2)，…，X(0)(n)}，通过累加生成新序列:X(1)={X(1)(1)，X(1)(2)，…，X(1)(n)}，累加生成的方法是:x(1)(k)=∑ki=1x(0)(i)，k=1，2，…，n。

2)建立模型:假定X(1)序列变化过程呈指数特性，则GM(1，1)模型相应的微分方程为其中α为发展灰数，μ 为内生控制灰数。将上式离散化，微分方程变为差分方程:x(0)(k)+αz(1)(k)=μ。式中

z(1)(k)= 0.5x(1)(k)+0.5x(1)(k -1)，k = 2，3，…，n Z(1)(k)为背景值，表示

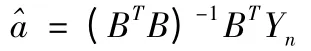
3)建立预测方式:求出参数α，μ 后，求解微分方程，即可得预测模型

1.2 ARMA 预测模型

ARMA 建模基本思路:将预测对象随时间迁移而形成的数据序列视为一个随机序列，用一定的数学模型来近似描述这个序列，模型通过识别后就可以从时间序列的过去值和现在值预测未来值。其一般形式为［6］

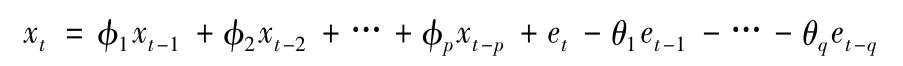
其中:p，q 分别为模型自回归和滑动平均部分的阶数;xt不仅包括自身t 时刻以前的有限项的加权和，还包括t 时刻以前有限项白噪声干扰量的加权和。此时，xt与它自身过去时刻值的相关参数不再是线性关系，而是非线性关系。当确定一个平稳随机序列可以用ARMA 模型进行描述以后，就需要对模型的阶数和参数进行辨识。为了便于在计算机上编程实现，参数的辨识通常采用递归的最小二乘法。

2 蚁群改进BP 神经网络

2.1 蚁群算法模型

蚁群算法(ant colony algorithm，ACA)是由意大利学者M.Dorigo［7］在20 世纪90 年代受到真实蚂蚁的觅食机制的启发而提出的一种新的群智能优化方法，是一种随机搜索算法。其算法模型为［8-9］

1)定义并且初始化人工蚁群集合Ω。

2)设定迭代次数或终止条件，开始循环迭代。

3)策略选择:将遵循一定状态转移规则。

4)局部信息更新规则:蚂蚁k 在每次周游中对它所经过的弧更新信息素:

5)全局信息更新规则:每次循环结束，所有的蚂蚁都完成一次周游，此时若产生新的最优解，则对当前最优解上的弧更新信息素:

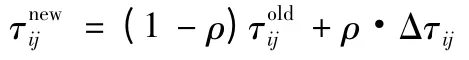
式中:Δτij为增加的信息素为更新后的弧上信息素为以前弧上的信息素;ρ 为［0，1］区间的常数，为信息素的挥发度系数。

6)满足迭代终止条件，输出结果。

2.2 BP 神经网络

BP 神经网络是指基于误差反向传播算法(BP 算法)的多层前向神经网络，其神经元采用的激活函数通常是Sigmoid 型可微函数，所以可以实现输入和输出间的任意非线性映射。BP 神经网络具有较好的非线性和自学习能力，目前研究结果显示了神经网络在非线性预测中的效果优于传统的时间序列建模技术［10-13］。但是它也有缺陷，如易出现振荡、陷入局部极值、收敛速度慢、初始权值、阈值和隐含层神经元个数难以确定等问题。为优化BP 算法，应用蚁群算法对其进行改进。

2.3 蚁群改进BP 神经网络

具体方法为:首先确定神经网络结构，输入层个数为n，隐层神经元数为m，输出层为p 个神经元。定义人工蚁群的可行解向量Xi，包括BP 神经网络的隐层单元m，输入和隐层连接权值W ∈Rn(m+1)及隐层与输出层的连接权值W ∈Rp(m+1)，输入节点阈值bki和输出节点阈值bko。然后用动态调整人工蚁群算法搜索最优可行解，选取N 个人工蚂蚁构成蚁群，每个人工蚂蚁都是D 维向量。人工蚂蚁初始群体随机产生后，以后各代人工蚂蚁的可行解根据人工蚂蚁完整周游的遍数而变化。用以下公式衡量每个人工蚂蚁的适应值

式中:yi是第i 个样本第j 个网络输出节点的理想输出值;yk是第i 个样本第j 个在BP 神经网络中输出节点的实际输出值;p 是输出节点数;n 是训练集样本数。该函数是一个具有多个极小点的非线性函数，则对该BP 神经网络的训练过程为调整BP 神经网络输入权值ωij、输出权值ωi0、输入节点阈值bki和输出节点阈值bko，直至解的适应度不再有意义地增加为止，此时即可得到精确的最优参数组合，也确定了最佳网络结构。

图1 蚁群算法优化神经网络

3 组合预测模型

1)分析数据，选择合适的单项预测模型与方法。本文选用了灰色预测和ARIMA 预测。

2)利用单项预测模型进行预测。

3)建立3 层BP 神经网络。输入层的节点数是单项预测模型的个数，输出层的节点数是问题目标的个数，隐层的节点数采取试错法来确定。

4)以单项模拟结果作为输入、实际数据作为目标输出，利用蚁群改进的BP 算法来训练并测试已建立的神经网络。

5)输入单项预测结果，利用训练好的神经网络进行预测。

图2 组合预测模型

4 应用对比

以某航空公司某航材历年消耗数量为例，取10 年的历史数据作为BP 网络的训练，另外选取4 年的历史数据作为测试数据，分别使用灰色预测方法、ARMA 预测方法、传统线性组合预测方法(利用最小二乘准则确定灰色预测和ARMA的最优权重)和基于蚁群改进BP 算法的组合预测方法进行预测，其预测误差曲线如图3 所示。其中曲线1 到4 分别表示灰色预测、ARMA 预测、传统线性组合预测、基于蚁群改进BP 算法的组合预测的误差。可以看出，基于蚁群改进BP 算法的组合预测方法在精度上有很大的优势。

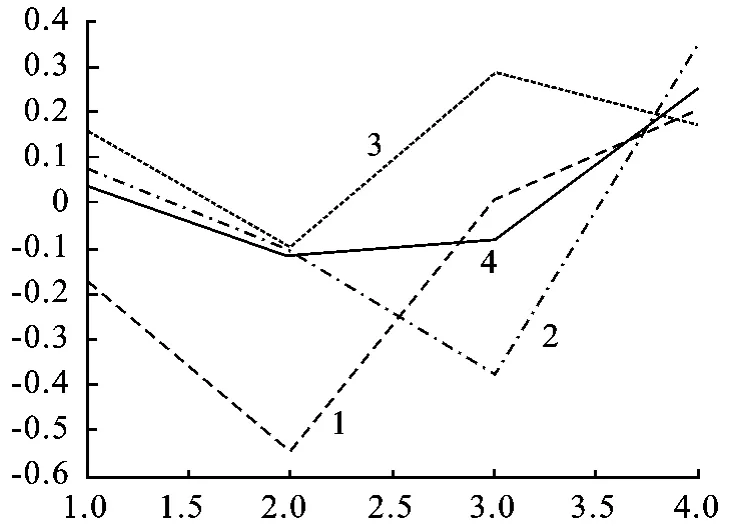
图3 预测误差曲线

5 结束语

本文所提出的蚁群改进BP 神经网络作为组合预测的实施载体，能够很好地发挥组合预测的预测效果，通过实例对比，可以看出基于蚁群改进BP 算法的组合预测方法在预测精度上优于单项预测方法和传统线性组合预测方法。

［1］Bates J M，Granger C W J.The combination of forcasts［J］.Operations Research Quarterly，1969，20(4):451-460.

［2］刘思峰，徐忠祥.灰色系统研究新进展［M］.武汉:华中理工大学出版社，1996:1-10.

［3］Deng J L.Control problems of grey systems［J］.Systems ＆Control Letters，1982，1(5):288-294.

［4］傅立.灰色系统理论及其应用［M］.北京:科学技术文献出版社，1992.

［5］Wen Kun-Li，Huang Yi-Fung，You Mei-Li，et al.The Development of GM(1，1) Error Toolbox［J］.IEEE International Conference on Intelligent and Advanced Systems，2007:276-279.

［6］黄一丹.NET 平台下汽车市场需求预测系统的研究与开发［D］.南京:东南大学，2009:15-18.

［7］Dorigo M，Maniezzo V，Colorni A.Ant system:optimization by a colony of cooperating agents［J］.IEEE Trans On Systems，Man and Cybernetics，Part B，1996，26(1):29-41.

［8］Donald K，Wedding II，Krzysztof J Cios.Time series forecasting by combining RBF networks，certainty factors，and the Box-Jenkins model［J］. Neurocomputing，1996( 10): 149-168.

［9］Victor R Prybutok，Junsub Yi，David Mitchell. Comparison of neural network models with ARIMA and regression models for prediction of Houston’s daily maximum ozone concentrations［J］.European Journal of Operational Research，2000(122):31-40.

［10］Colorni A，Dorigo M，Maniezzo V.The Ant System:Optimization by a Colony of Cooperating Agents［J］. IEEE Trans on Systems，1996，26(1):1-13.

［11］叶强. 基于改进蚁群算法的一类单机调度问题研究［D］.合肥:合肥工业大学，2008.

［12］钟娟，赵彦强，孙富康，等.基于混合蚁群算法的物流配送路径问题［J］.合肥工业大学学报:自然科学版，2009，32(5):686-688.

［13］王金山，杨国超. 基于灰色可变加权系数的组合预测模型［J］.四川兵工学报，2011(12):117-119.