大长径比弹箭流场模拟与气动力分析
2012-07-09彭志凌王志军
彭志凌,王志军
(中北大学 机电工程学院,太原 030051)
弹箭气动力参数一般通过经验计算和风洞吹风取得。经验计算主要借助计算公式和经验数值获得气动力参数,速度快,成本低,但由于所计算的气动力外形往往比较复杂,仅靠现有的计算公式和经验数值不能满足要求。对于型号研发,通过风洞实验获取气动力参数是必不可少的过程,但是风洞实验非常昂贵,很多预研项目难以支付该笔费用,所以利用软件计算和分析气动力是必要的手段。
1 建立火箭弹模型
利用Gambit 建模如图1 所示,火箭弹以超音速飞行,周围流场是三维、有粘的。因此,采用理想可压缩气体模型,为了简化计算,采用层流模型,控制方程采用无量纲N -S 方程,流动为定常流动。

图1 某火箭弹模型
2 非结构化网格划分
为了灵活方便地数值模拟绕复杂外形的流动,在20 世纪80 年代末人们提出了采用非结构网格的技术手段,现已成为研究的热点之一。所谓非结构网格就是指这种网格单元和节点彼此没有固定的规律可循,其节点分布完全是任意的。其基本思想基于这样的假设:任何空间区域都可以被四面体(三维)或三角形(二维)单元所填满,即任何空间区域都可以被四面体或三角形为单元的网格所划分。
弹箭外形比较复杂,在这种情况下,非结构化网格是一个很好的选择。将流场分为内外两层,如图2 ~图4 所示。

图2 某火箭弹流场网格示意图

图3 某火箭弹内层流场网格示意图

图4 流场网格示意图
由于该火箭弹是轴对称的,为了减少计算时间,提高计算效率,取火箭弹的一半进行计算。图2 中的外层流场区域是直径3.6 m,长度7.2 m 的圆柱区域。内层区域是直径1.080 m,长度为3.6 m 的圆柱形区域。内层区域网格划分较细,外层区域网格划分较粗。这样既保证了计算的准确性,又减少了计算量。
3 数学模型
划分网格后,用Fluent 软件进行计算。此处的湍流模型采用三维k-ε 双方程模型。连续方程

动量方程即雷诺平均的Navier-Stockes 方程

k-ε 双模型方程标准型如下:
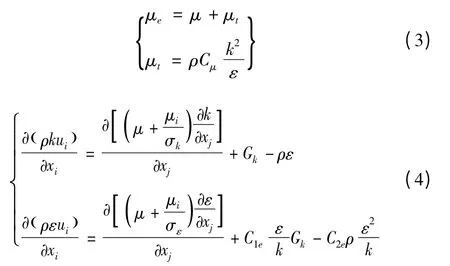
4 计算方法
为了节省内存,在此选用显示格式求解器。湍流模型选用Spalart-Allmaras,这是因为Spalart-Allmaras 模型是一个相对简单方程模型,只求解有关涡粘性的输运方程,计算量相对较小。比较适合于具有壁面限制的流动问题,在对飞行器、翼型等绕流的流场分析中能够给出很好的计算结果。
考虑到大长径比弹箭的飞行速度超过音速,所以流体应为可压缩气体。为了满足气体状态方程,选取流体类型为ideal-gas;壁面条件为无滑移条件,壁面粗糙度为0.5;数值计算过程中差分格式选用standard 方法。压力-速度耦合采用SIMPLEC;动量、湍流动能、湍流耗散率选用二阶迎风格式second order upwind scheme;松弛因子为0.3,密度、质量力为1,动量项为0.5,湍流能项为0.6,湍流耗散率项为0.6,湍流粘性项为0.6;以气动力的收敛情况来控制收敛。
5 气动力仿真迭代收敛过程和弹体压力分布
经过5 000 次迭代后,力和力矩的监视曲线基本不再变化,计算基本收敛,见图5 ~图7 所示,弹体压力云图见图8。
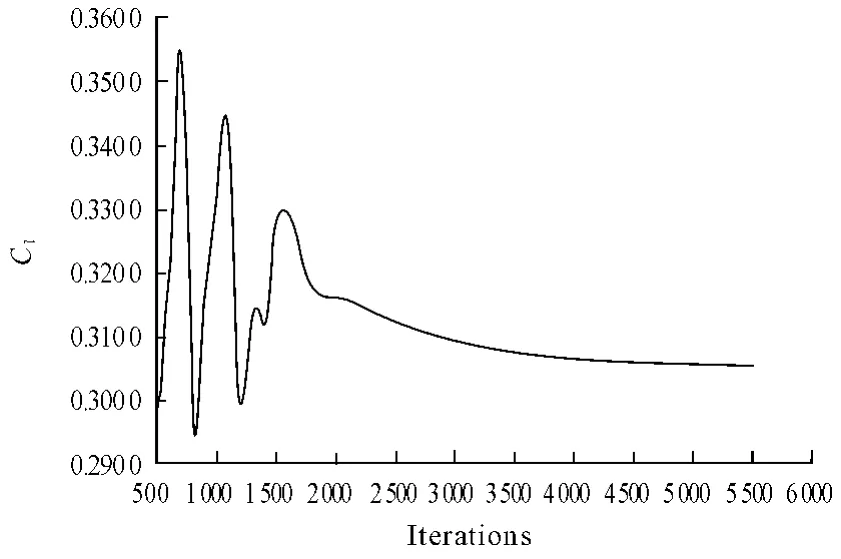
图6 升力系数随迭代过程变化曲线

图7 俯仰力矩系数随迭代过程变化曲线

图8 弹体压力分布云图
6 结果分析
以长径比为20 的火箭弹为例,运用Fluent 软件对不同攻角和不同飞行速度下的阻力系数、升力系数和俯仰系数进行了仿真,见图9 ~图11 所示。
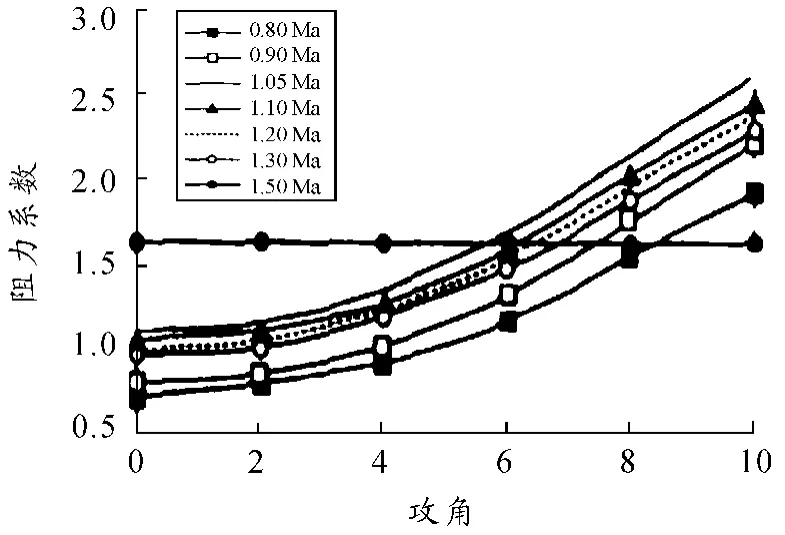
图9 阻力系数曲线

图10 升力系数曲线

图11 俯仰力矩系数曲线
7 结束语
本文以长径比为20 的火箭弹为研究对象,利用CFD 软件模拟了弹箭流场情况,通过仿真,分析了该火箭弹的气动力,并得出了不同攻角和不同飞行速度下的阻力系数、升力系数和俯仰系数的变化规律。
[1]张来平,呙超,张涵信,等.任意平面域的三角形网格和混合网格生成[J].空气动力学报,1999,17(1):8-14.
[2]孙少鹏,杨炸生.非结构网格生成技术的研究[J].空气动力学报,1996(1):19-25.
[3]王福军.计算流体动力学分析一软件原理与应用[M].北京:清华大学出版社,2004.
[4]蒋跃文,张伟伟,叶正寅.基于CFD 技术的流场/结构时域耦合求解方法研究[J].振动工程学报,2007,20(4):396-400.
