反潜机雷达离散搜潜效率建模

朱伟良，野学范，胡 轶

(海军潜艇学院，山东 青岛 266042)

反潜机使用雷达搜潜时通常采用检查性搜索，其飞行速度快，搜索海域广，效率高，对潜攻击能力强，是潜艇的“天敌”［1-2］。常规潜艇由于必须定期浮起充电和通风，极易被敌反潜机雷达发现［3-4］。反潜机搜潜时通常有离散搜索和连续搜索2 种工作方式。为防止雷达信号被潜艇雷达侦察仪截获，反潜机在使用雷达搜潜时一般采用离散搜索［5］。其一次发射雷达信号，搜索面积一定，由雷达自身装备性能决定。研究雷达搜潜效率的关键是计算反潜机雷达在单位时间内离散搜索的有效面积。有效搜索面积除受雷达自身装备性能制约外，还与潜艇与反潜机的相对位置密切相关，并随着反潜机速度、雷达探测距离和相邻2 次发射信号之间的距离变化而变化。本文基于上述分析，从反潜机雷达有效搜潜面积入手建立了离散搜潜效率数学模型，可为潜艇海上作战规避搜索，保持隐蔽性提供参考依据。

1 反潜机雷达搜潜特点分析

反潜机使用雷达发现潜艇的必要条件是，在雷达探测范围内，潜艇处于可被雷达发现的状态，即通气管航行状态、潜望状态、半潜状态或水面状态。如果潜艇的活动海域足够大，潜艇处于其他隐蔽状态下，则潜艇与反潜机不能相互发现。对反潜机而言，潜艇何时何地处于暴露性状态是随机现象，而且这种随机性在时间上是均匀的［6］。在反潜机使用雷达搜潜期间，潜艇处于雷达可发现状态的时间系数Kt可由式(1)计算

式中:ti表示反潜机雷达搜索期间，潜艇处于潜望状态(i =1)、半潜状态(i=2)、通气管状态(i =3)和水面状态(i =4)的时间。

设反潜机搜索航速为V，雷达发现潜艇距离为Dlf，潜艇位置在反潜机搜索海域S 内服从均匀分布，潜艇雷达侦察仪截获反潜机雷达信号的距离为Dj(通常认为潜艇雷达侦察仪截获到反潜机雷达信号即代表潜艇发现了反潜机)，此时潜艇与反潜机之间的水平距离为Dqf(即潜艇发现反潜机的距离)，潜艇速度为v。

为防止反潜机雷达信号被潜艇雷达侦察仪截获，反潜机一般进行离散型搜索，即间断工况搜索，如图1 所示。通常情况下，Dqf＞Dlf。假设反潜机在A 点发射雷达信号，一次发射信号的搜索面积为πD2lf，此时:①若潜艇在以A 为圆心，Dlf为半径的圆内将被反潜机发现;②若潜艇与反潜机之间的距离大于Dlf且小于Dqf，则潜艇将可截获反潜机雷达信号而潜入水下，反潜机不能探测到潜艇;③若潜艇与反潜机之间的距离大于Dqf，则双方互不发现。

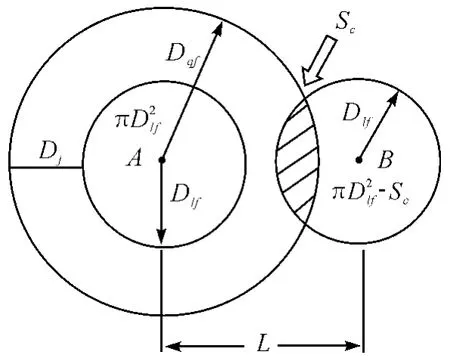
图1 雷达离散搜索示意

2 反潜机雷达搜潜效率模型

2.1 有效搜潜面积

假定选择下一个雷达发射点为B 点，A 与B 之间的距离为L，如图1 所示。若2 点之间的距离L 小于Dqf+Dlf，位于阴影区SC内的潜艇在前1次雷达发射信号后即潜入水下，阴影区SC成为无效的搜索区域，则本次发射信号的有效搜索面积为πD2lf-SC;反之，如果L 大于Dqf+Dlf，则反潜机会遗漏一部分海区，且L 增大，反潜机雷达的搜潜效率越低［7］。综上所述，单位时间内雷达的有效搜索面积是反潜机速度、雷达探测距离和相邻2 次发射信号之间距离的函数。

设雷达一次发射搜索的有效面积为A(L)，令Dlf= r，Dqf=R，如图2 所示，则一次发射搜索的有效面积可记为

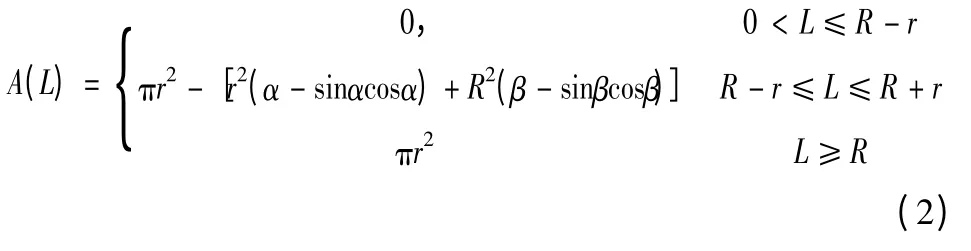
其中:

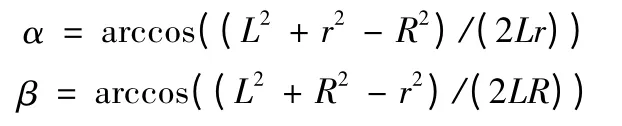
图2 雷达一次发射信号搜索面积示意图

设单位时间内雷达搜索的有效面积为B(L)，由于反潜机搜索速度远大于潜艇速度，则反潜机与潜艇之间的相对速度V'可近似为反潜机速度Vj，令V' =v，则有

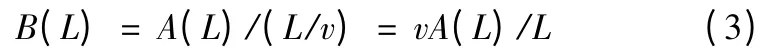
从式(3)可以看出，当反潜机搜索速度和雷达发现距离固定时，单位时间内有效搜索面积仅取决于相邻2 次发射信号时反潜机之间的距离L。令b(L)=A(L)/L，则有

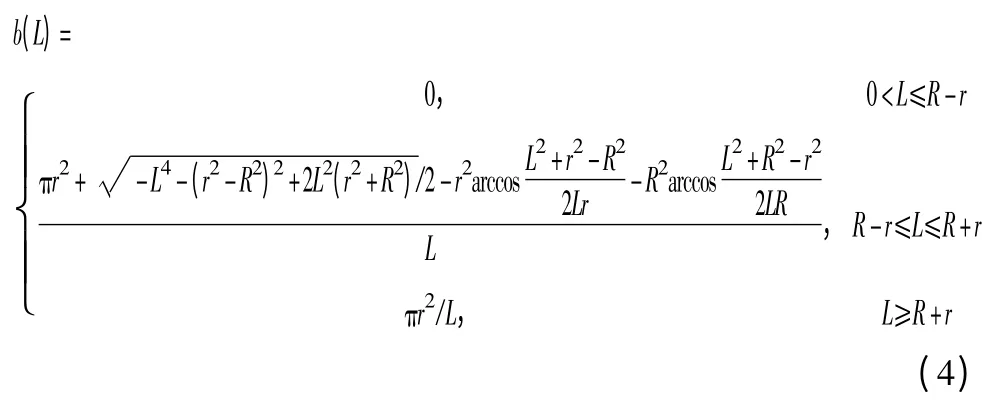
式中，b(L)为L∈［0，+∞)上的连续函数，从而:

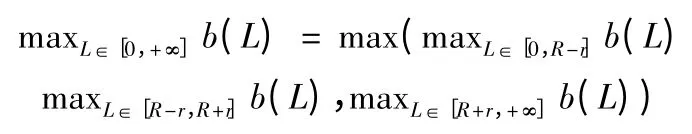
化简可得

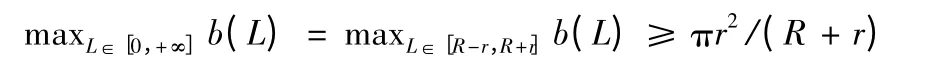
记R/r=k，L/r=x，当R-r≤L≤R+r 时，记g(x，k)=b(L)，则有

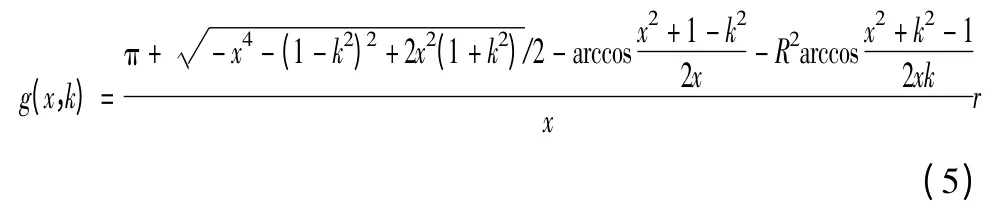
其中，k-1≤x≤k+1，令f(x，k)=g(x，k)/r，对于具体型号的反潜机雷达和潜艇雷达侦察仪，一般R，r 为常数，即k 为固定值，且k≥1，则f(x，k)值仅取决于x。令f(x，k)在x=x0处取得极大值a(k)，即

则反潜机雷达单位时间内有效搜索面积U 的最大值Q(r，R，v)为

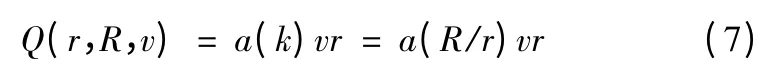
2.2 近似简化

由于上述函数过于复杂，难以直接给出a(k)的表达式，因此可先采用计算机解算出不同k 值下函数f(x，k)的近似极大值f(x0，k)，再用数据拟合的方法得出a(k)的表达式。采用计算机解算出k—f(x0，k)近似值，见表1;将近似值用Matlab 绘出a(k)的曲线，如图3 所示。

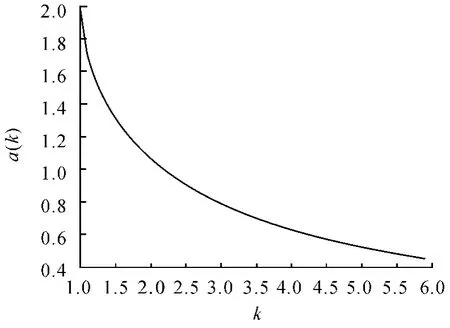
图3 a( k) 的近似曲线

设a(k)的表达式为

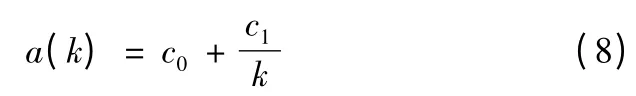
采用最小二乘拟合，结果为

将式(9)代入式(7)，表达式不够简练，为此拟找出a(k)的近似表达式。当L=R+r 时，即x=k+1，从式(5)可以看出，此时函数f(x，k)的最大值z(k)为

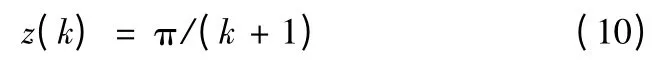
因此可进行以下近似

2.3 数值比对

对比不同k 值时的z(k)与a(k)值，结果如表2 所示。当k 为1.5 时，绝对误差约为7%，相对误差约为5%;而当k ＞2.5时，绝对误差与相对误差均小于1.2%。

表1 计算机解算的k—f( x0，k) 近似值

表2 不同k 值下z( k) 值与a( k) 值及差值

采用Matlab 绘出z(k)、a(k)曲线，如图4 所示。

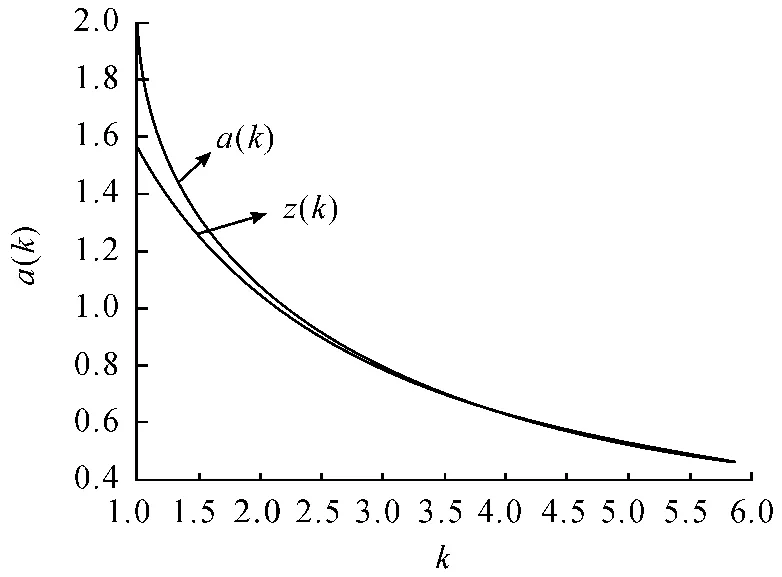
图4 z( k) 与a( k) 曲线

由图4 可以看出:当k ＞2.5 时，2 条曲线几乎吻合，完全可以用z(k)代替a(k);而当1.5 ＜k ＜2.5 时，也可用z(k)近似代替a(k)。由于通常潜艇雷达侦察仪发现反潜机距离大于雷达发现潜艇距离的1.5 倍以上，因此式(11)的近似误差很小，可忽略不计。

当反潜机采用近似最优搜索间距(k +1)r = R + r 时，则有

2.4 效率模型

由于反潜机雷达搜潜效率受天气影响较大，因此模型必须考虑天气影响系数Kw。同时，当潜艇位于雷达探测范围时，雷达并非一定能与潜艇建立接触，所以还必须考虑雷达与潜艇接触概率P。综合以上因素，反潜机使用雷达在离散方式下搜潜效率U 为

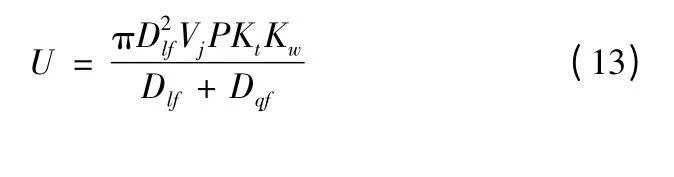
3 结束语

本文从反潜机雷达有效搜潜面积入手，建立了离散搜索方式下反潜机雷达搜潜效率数学模型，并在一定误差范围内对模型进行了简化，使之更便于计算。该模型为潜艇海上作战，尤其是潜艇在通气管航行状态、潜望状态等暴露性状态中，灵活规避反潜机雷达搜索，保持潜艇隐蔽性提供了重要的参考依据。通过该模型还可以进一步建立反潜机雷达发现潜艇概率数学模型。因此，反潜机雷达搜潜效率模型具有较大的战术价值。

［1］周贺，吴勇.某型潜用雷达侦察机对反潜反潜机雷达信号侦察方法初探［J］. 潜艇学术研究，2001，19(4):35-36.

［2］薛涛，楼晓平，张文玉.潜艇应对高空反潜作战的对策分析［J］.潜艇学术研究，2009(4):31-34.

［3］吴芳，吴铭，杨日杰.反潜机吊放声纳扩展螺旋线形搜潜建模［J］. 北京航空航天大学学报，2011，37(9):1137-1141.

［4］谭安胜，胡峥涛，贺凯.驱护舰编队对海作战中舰载无人机任务规划［J］.指挥控制与仿真，2011，33(5):1-3.

［5］胡轶.常规潜艇规避反潜直升机搜索研究［J］.潜艇学术研究，2005，23(2):10-12.

［6］陆铭华.舰艇作战模拟理论与方法［M］.北京:海洋出版社，2002:21-23.

［7］赵绪明，孙明太.吊放声纳搜索效率模型探讨［J］.电光与控制，2005，12(2):37-41.