立式U型管自然循环蒸汽发生器1次侧流体流经U型管段重力压降计算
2012-07-09饶彧先张杨伟
饶彧先,蔡 琦,张杨伟
(海军工程大学 船舶与动力学院,武汉 430033)
自然循环因其结构简单、换热能力强、非能动等特点,在核动力领域有着重要的应用前景。尤其对核动力舰船来说,反应堆装置自然循环能力高时,可保证舰船在中、低速下不使用主泵,从而可免去由主泵引起的一系列问题,如主泵断电事故和衰变热导出等,保证堆芯不产生过热而烧毁。在含有立式U型管自然循环蒸汽发生器的循环回路中,能否准确计算流体流经U型管段的重力压降对确定自然循环工况下回路自然循环能力至关重要。在使用现有一些大型电站系统分析程序(如RELAP5 等)处理此类问题时,常按固定网格法将U型管直管段按等长度进行控制体划分[1],弯管段等效成直管段[1]或者等效成与水平方向夹角为45°的斜管段[2]进行处理。由于U型管管内温度随U型管管长分布是非线性的[3],如果在温度变化较大处控制体长度划分过大,再加上对弯管段的近似处理,这样计算得到的重力压降准确性将降低。为此,文献[4]和文献[5]采用移动边界法将控制体长度按变量处理,但是却将每1 换热区域只划分为1 个控制体,没有进一步对换热区域进行控制体划分。
本文借鉴移动边界法,将蒸汽发生器1次侧U型管内各换热区域按等温度差值进行控制体划分,按实际的几何关系处理U型管弯管段,建立蒸汽发生器1次侧流体流经U型管段的重力压降计算模型,并输入大亚湾核电厂蒸汽发生器热工参数值进行计算分析。此外,还对U型管束直管段高度、内径和管间距进行了参数敏感性分析,为合理选择参数以提高回路自然循环驱动压头和自然循环能力提供参考。
1 数学模型
如图1 所示,每根U型管沿轴向从中间分开,分为热侧和次热侧;将蒸汽发生器2 次侧热力区划分为3 个区域,即热侧单相换热区、次热侧单相换热区和两相沸腾换热区[6];U型管内1次侧流体相应也划分为3 个区域,分别为Ⅰ区、Ⅱ区和Ⅲ区。在上述区域划分的基础上,对计算进行了如下简化和假设:①U型管传热简化为直管段传热,蒸汽发生器内的传热和流动均为稳态,各U型管换热面积、管内1次侧流体质量流量均相等,单管与流体的传热遵从对数温差传热规律[7];②循环水与给水在蒸汽发生器底部均匀混合,热侧单相换热区与次热侧单相换热区内2 次侧流体质量流量相等,且两区之间无能量交换;③热侧单相换热区与次热侧单相换热区只考虑流体横掠管束换热,两相沸腾换热区仅考虑大空间饱和核态沸腾换热,不考虑传热在径向上的分布;④2 次侧排污及其他流量损失忽略不计,1次侧流量损失忽略不计,蒸汽发生器与周围环境之间的热损失忽略不计。
1.1 U型管内一次侧流体温度分布计算
U型管内1次侧流体温度分布计算是进行蒸汽发生器1次侧流体U型管段重力压降计算时需首先解决的问题。给定2 次侧边界条件及U型管束换热面积、1次侧压力和流经蒸汽发生器流体质量流量,将1次侧流体U型管入口温度赋初值,根据能量守恒定律计算1次侧流体U型管内Ⅰ、Ⅱ、Ⅲ区段进出口温度,如下:
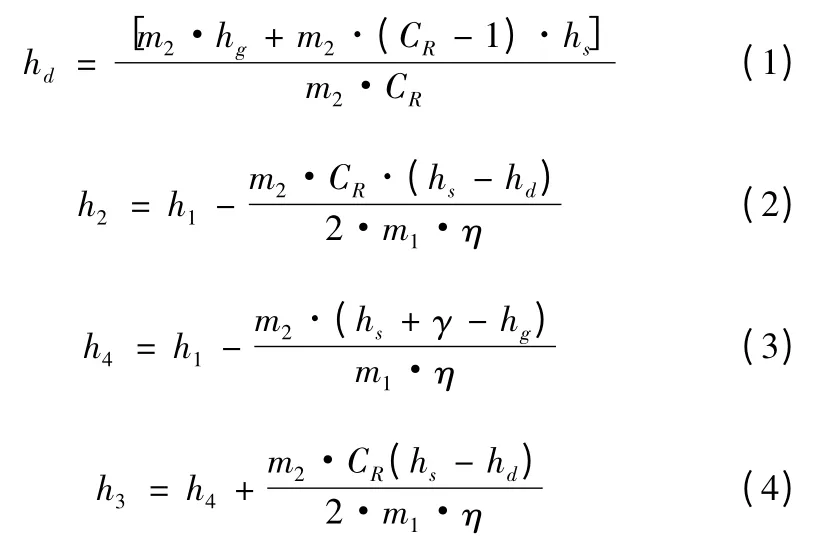
式中:m1为1次侧流体质量流量(kg/s);m2为2 次侧给水质量流量(kg/s);CR为循环倍率;η 为传热效率;h1为U型管入口比焓和Ⅰ区入口比焓(kJ/kg);h2为Ⅰ区出口比焓和Ⅲ区入口比焓(kJ/kg);h3为Ⅲ区出口比焓和Ⅱ区入口比焓(kJ/kg);h4为Ⅱ区出口比焓和U型管出口比焓(kJ/kg);hg为给水比焓(kJ/kg);γ 为2 次侧压力下水的汽化潜热(kJ/kg);hs为2 次侧压力下饱和水的比焓(kJ/kg);hd为蒸汽发生器底部给水与循环水混合后2 次侧水的比焓(kJ/kg)。将上述方程左边的焓值转化为温度值即可完成各换热区进出口温度计算。
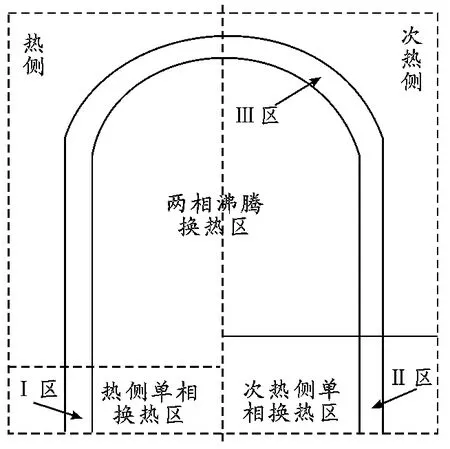
图1 蒸汽发生器热力分区
对U型管内Ⅰ、Ⅱ、Ⅲ区按等温度差值划分控制体,即换热区内各控制体进出口温差相等,但各控制体长度不一定相等;U型管金属,2 次侧热力区划分成与1次侧相对应的控制体;根据能量守恒定律和对数温差传热规律计算U型管内各控制体换热面积并求和得出U型管束换热面积,如下:
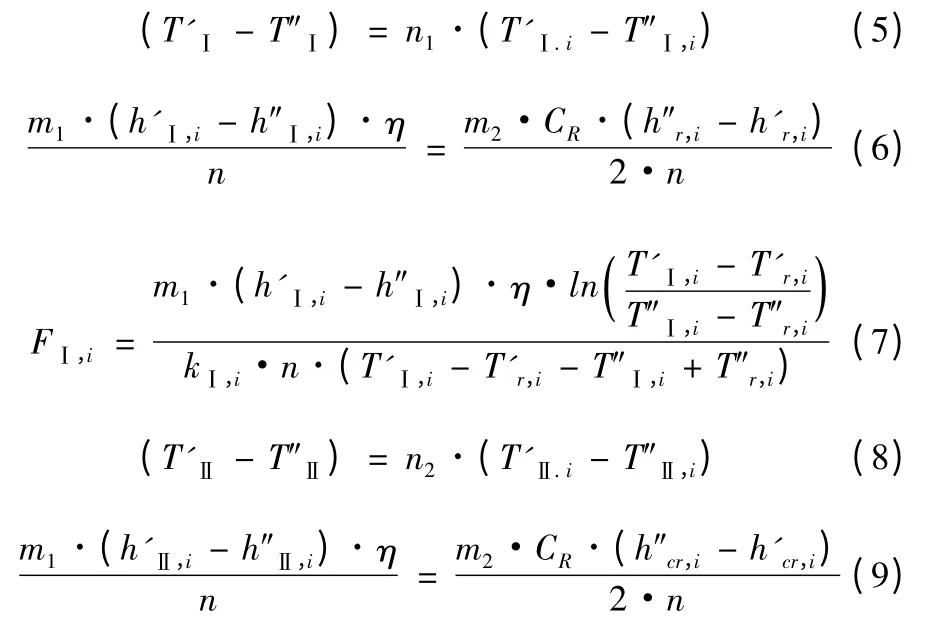
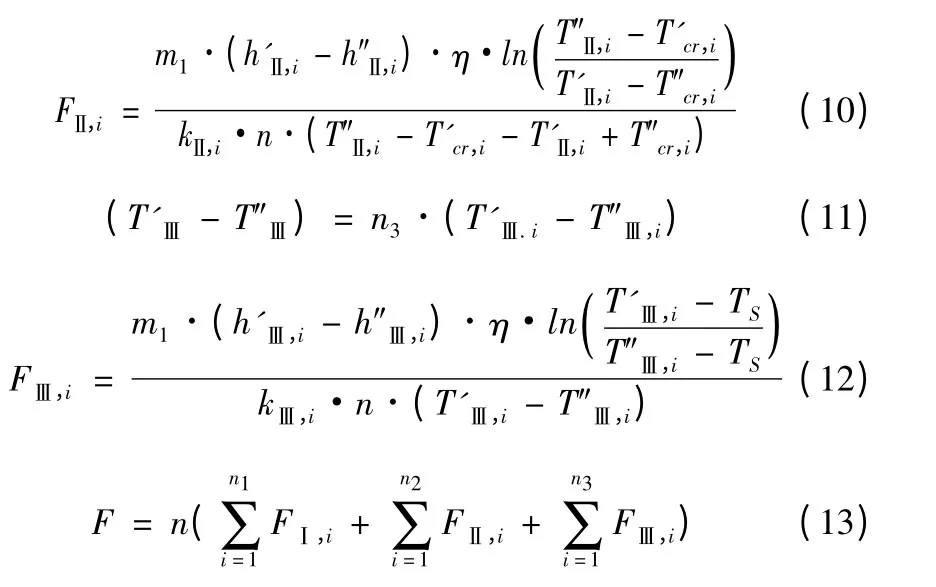
式中:T'Ⅰ,T'Ⅱ和T'Ⅲ分别为Ⅰ、Ⅱ、Ⅲ区进口温度(K);T″Ⅰ,T″Ⅱ和T″Ⅲ分别为Ⅰ、Ⅱ、Ⅲ区出口温度(K);T'Ⅰ.i,T'Ⅱ.i和T'Ⅲ.i分别为Ⅰ、Ⅱ、Ⅲ区第i 个控制体的进口温度(K);T″Ⅰ,i,T″Ⅱ,i和T″Ⅲ,i分别为Ⅰ、Ⅱ、Ⅲ区第i 个控制体的出口温度(K);TS为2 次侧压力下水的饱和温度(K);T'r.i和T'cr.i分别为2 次侧热侧、次热侧换热区第i 个控制体的进口温度(K);T″r.i和T″cr.i分别为2 次侧热侧、次热侧换热区第i 个控制体的出口温度(K);h'Ⅰ.i,h'Ⅱ.i和h'Ⅲ.i分别为Ⅰ、Ⅱ、Ⅲ区第i个控制体的进口比焓(kJ/kg);h″Ⅰ.i,h″Ⅱ.i和h″Ⅲ.i分别为Ⅰ、Ⅱ、Ⅲ区第i 个控制体的出口比焓(kJ/kg);h'r.i和h'cr.i分别为2 次侧热侧、次热侧换热区第i 个控制体的进口比焓(kJ/kg);h″r.i和h″cr.i分别为2 次侧热侧、次热侧换热区第i个控制体的出口比焓(kJ/kg);n 为U型管数目;n1,n2和n3分别为Ⅰ、Ⅱ、Ⅲ区段控制体数目,计算中n1=n2=5,n3=30;FⅠ,i,FⅡ,i和FⅢ,i分别为Ⅰ、Ⅱ、Ⅲ区第i 个控制体对应U型管段换热面积(m2);F 为U型管束换热面积计算值(m2);kⅠ,i,kⅡ,i和kⅢ,i分别为Ⅰ、Ⅱ、Ⅲ区第i 个控制体对应传热系数(kW/(m2·K))。
将U型管束传热面积计算值同实际值相比较,调整U型管入口温度大小,直至U型管束传热面积计算值满足

式中:F'为U型管束换热面积实际值(m2);ε 为迭代收敛常数,计算中ε 取为0.1%。
1.2 U型管内Ⅰ、Ⅱ、Ⅲ区段重力压降计算
将Ⅰ、Ⅱ、Ⅲ区段各控制体进出口温度取算术平均值作为该控制体温度,求出该控制体密度,分别计算出U型管内1次侧流体流经Ⅰ、Ⅱ、Ⅲ区段的重力压降。Ⅰ、Ⅱ区段均为直管段,Ⅰ区段在热侧、Ⅱ区段在次热侧,重力压降计算如下:
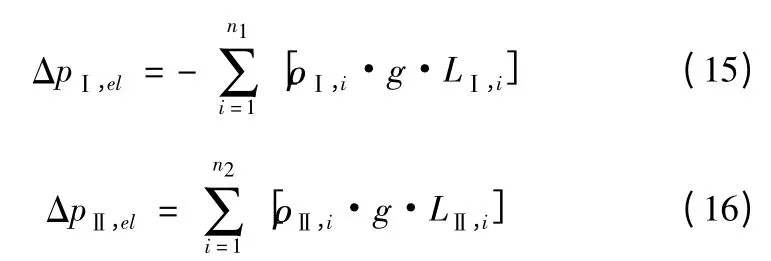
式中:ΔpⅠ,el和ΔpⅡ,el分别为1次侧流体流经Ⅰ、Ⅱ区段的重力压降(Pa);ρⅠ,i和ρⅡ,i分别为Ⅰ、Ⅱ区第i 个控制体密度(kg/m3);LⅠ,i和LⅡ,i分别为Ⅰ、Ⅱ区第i 个控制体长度(m);g 为重力加速度,g=9.8 m/s2。
Ⅲ区段既包括直管段,又包括弯管段。如图2 所示,弯管段第i 个控制体竖直方向上高度变化ΔLi可由几何关系给出:
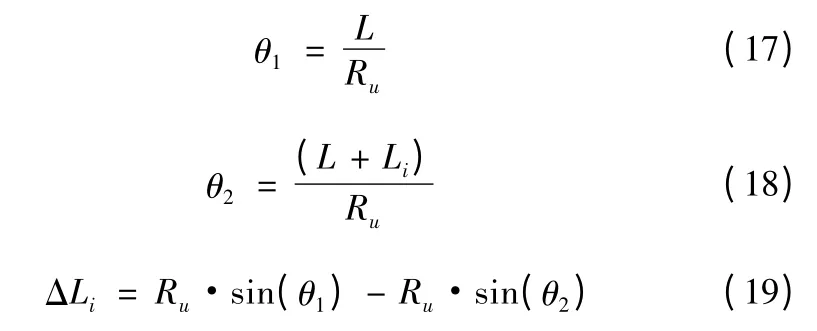
式中:ΔLi为弯管段第i 个控制体竖直方向上的高度变化,正值表示控制体入口位置高于出口位置(m);Li为第i 个控制体长度(m);L 为第i 个控制体入口位置距弯管段起始点弧长(m);Ru为U型管弯曲半径(m);θ1和θ2为圆心角(rad)。
分别计算直管段热侧、直管段次热侧和弯管段的重力压降并求和,Ⅲ区段重力压降计算如下:


图2 U型管弯管段几何关系
对Ⅰ、Ⅱ、Ⅲ区段重力压降求和得出1次侧流体流经U型管段的重力压降:
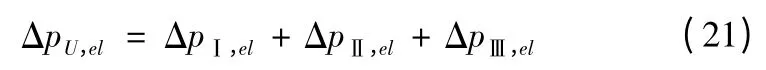
式中:ΔpU,el,ΔpⅠ,el,ΔpⅡ,el和ΔpⅢ,el分别为1次侧流体流经U型管段、Ⅰ、Ⅱ、Ⅲ区段的重力压降(Pa)。
1.3 换热模型
1次侧各区段管内强迫对流换热系数计算采用Gnielinski 公式[7]。与Dittus-Boelter 公式相比,Gnielinski 公式本身已考虑温差及长径比的影响。文献[7]指出,当需要较高的计算准确度时推荐使用Gnielinski 公式;2 次侧热侧、次热侧单相流体横掠管束对流换热系数计算采用Zhukauskas 公式[7],大空间饱和核态沸腾换热系数计算采用Kutateradze 公式[8]。
2 计算结果及分析
在上述数学模型基础上,使用fortran90 语言编制计算程序,选取大亚湾核电厂蒸汽发生器进行计算。大亚湾核电厂蒸汽发生器基本参数见文献[3],将2 次侧相关参数、U型管束换热面积、1次侧压力和流经蒸汽发生器流体质量流量作为输入参数,计算结果如表1 和图3 所示。
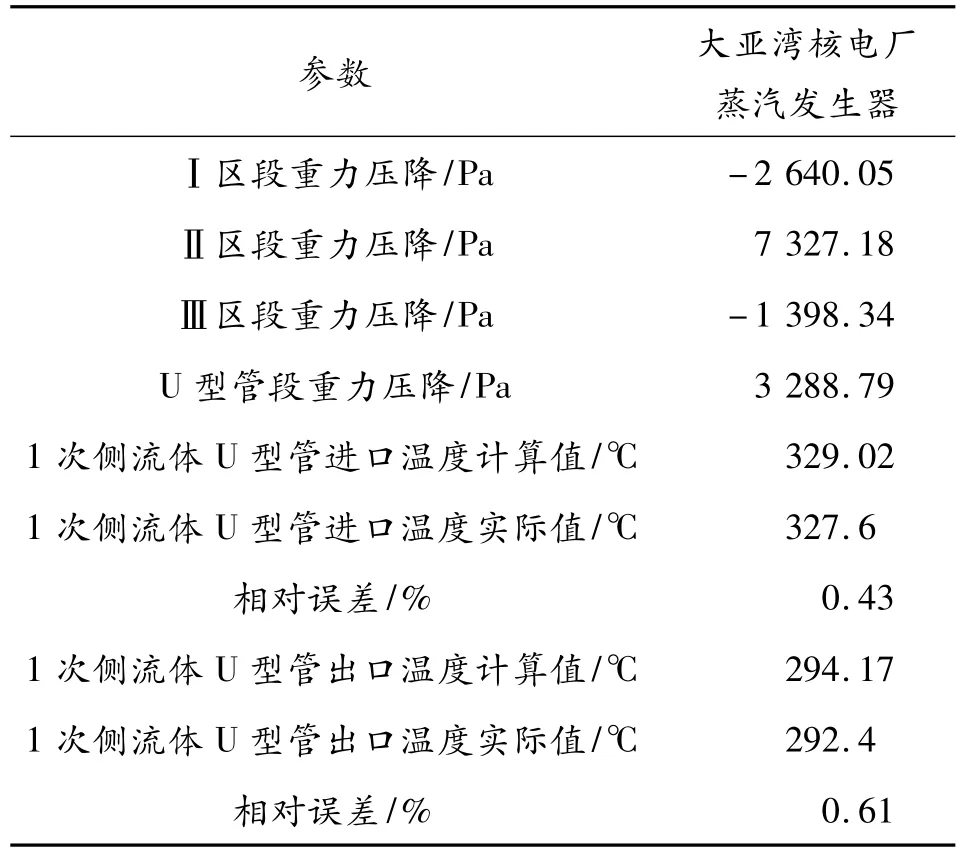
表1 U型管段重力压降计算结果
表1 中,1次侧流体U型管进出口温度计算值与实际值符合良好,验证了计算的正确性。1次侧流体Ⅰ、Ⅲ区段重力压降均为负值,Ⅱ区段重力压降为正值;靠近U型管出口处,1次测流体密度较大,所以Ⅱ区段重力压降在U型管段重力压降中所占比重大。在Ⅰ、Ⅲ区段,各控制体与2 次侧传热温差沿1次侧流动方向逐渐减小,所以如图3 所示,控制体长度沿1次侧流体流动方向逐渐增大;在Ⅱ区段,各控制体与2 次侧传热温差沿1次侧流体流动方向逐渐增大,如图3 所示,控制体长度沿1次侧流体流动方向逐渐减小;计算结果同上述理论分析一致,表明了计算的合理性。
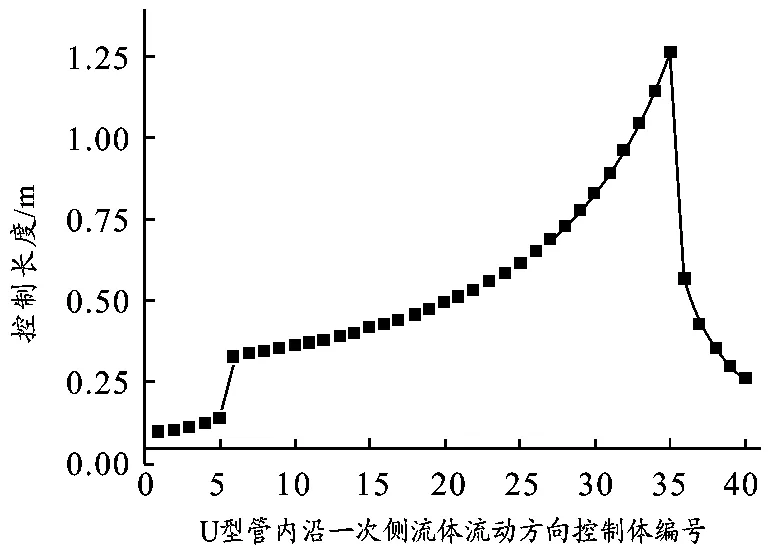
图3 U型管内控制体长度分布
3 参数敏感性分析
在确定的2 次侧相关参数、U型管束换热面积、1次侧压力和流经蒸汽发生器流体质量流量的条件下,选取U型管束直管段高度、U型管内径和管间距进行参数敏感性分析。
由图4 可看出,U型管束换热面积不变,管束直管段高度增加,管束总高增加,U型管段重力压降随之增加。当直管段高度由5 m 增加到8 m 时,U型管段重力压降增加约4.5%。
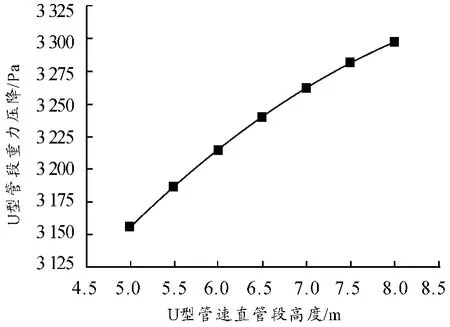
图4 U型管段重力压降随直管段高度的变化规律
U型管内径减小可减小传热系数,增大1、2 次侧传热温差;2 次侧压力不变的条件下,增加1次侧流体平均温度;如图5 所示,U型管段重力压降随U型管内径增加而减小。在图5 所示区间内,U型管段重力压降变化幅度为5.3%。
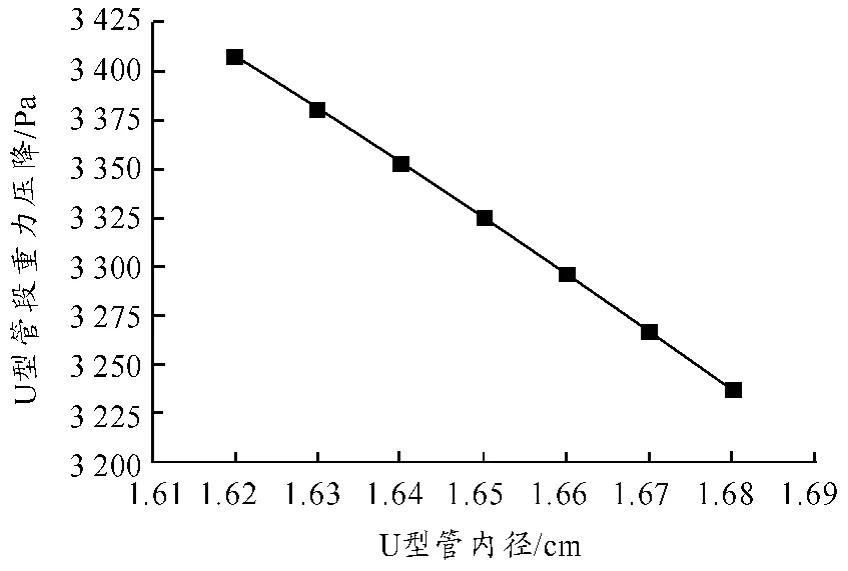
图5 U型管段重力压降随管内径的变化规律
如图6 所示,U型管段重力压降随U型管间距增加而增加。但在图示区间内,U型管段重力压降变化幅度太小,基本不变。在含有立式U型管自然循环蒸汽发生器的循环回路中,提高U型管段重力压降可提高回路自然循环驱动压头,增加回路自然循环能力;U型管束直管段高度、内径的改变对U型管段重力压降的改变较为明显,因此,在2 次侧相关参数、U型管束换热面积、1次侧压力和流经蒸汽发生器流体质量流量已确定的条件下,合理选择U型管管束直管段高度和内径对提高回路自然循环驱动压头,增加回路自然循环能力具有一定意义。
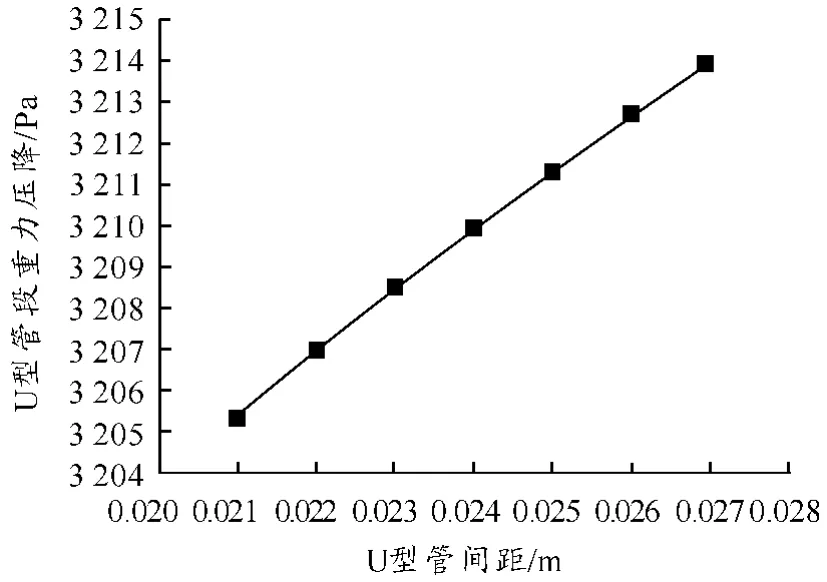
图6 U型管段重力压降随管间距的变化规律
4 结束语
本文建立了准确计算蒸汽发生器1次侧流体流经U型管段重力压降的数学模型,并将大亚湾核电厂蒸汽发生器热工参数作为输入值进行了计算和参数敏感性分析。计算结果与理论分析相一致。敏感性分析结果可为合理选择参数以提高回路自然循环驱动压头和自然循环能力提供参考。
[1]陈国伟,唐胜利,吴小飞.蒸汽发生器的RELAP5 仿真分析[J].机电设备,2009,9(5):23-26.
[2]鄢炳火,于雷,张杨伟,等.简谐海洋条件下自然循环运行特性[J].原子能科学技术,2009,43(3):230-236.
[3]孙中宁.核动力设备[M].哈尔滨:哈尔滨工程大学出版社,2003:83-104.
[4]张贵勤,单建强.整体式预热器U型管蒸汽发生器数学模型及动态模拟[J]. 核动力工程,1995,16( 2): 171-176.
[5]杨晨,唐胜利,何祖威.U型管蒸汽发生器数学模型的建立及其仿真研究[J]. 系统仿真学报,1999,11(3):167-171.
[6]王盟,王建军,孙中宁,等.蒸汽发生器最优化设计[J].核动力工程,2011,32(1):29-33.
[7]杨世铭,陶文铨.传热学[M].4 版.北京:高等教育出版社,2006:112-234.
[8]《蒸汽发生器》编写组.蒸汽发生器[M].北京:原子能出版社,1982:98-99.
