水下固体火箭发动机的负推力现象研究①
2012-07-09唐嘉宁李世鹏王宁飞
唐嘉宁,李世鹏,王宁飞
(北京理工大学宇航学院,北京 100081)
水下固体火箭发动机的负推力现象研究①
唐嘉宁,李世鹏,王宁飞
(北京理工大学宇航学院,北京 100081)
针对水下固体火箭发动机工作环境压强高的特点,结合固体推进剂的燃烧特性,采用UDF方法定义喷管入口边界条件,建立了固体推进剂燃气质量生成与水下超音速气体射流的耦合计算模型。将该模型的计算结果与水下固体火箭发动机的实验测量结果进行对比,验证了该模型的合理性。研究发现,水下固体火箭发动机在点火初期会出现负推力现象,负推力产生的原因是发动机点火初期,喷管内被过度压缩的燃气冲出喷管后,在喷管尾部形成一个超音速燃气泡,超音速流动使泡内压强降低;同时受到流动惯性作用的影响,气泡持续膨胀使泡内压强进一步大幅降低,发动机前后端面上的压差最终导致负推力现象产生。
水下固体火箭发动机;负推力;水下气体射流;多相流
0 引言
固体火箭发动机以其结构简单、操作使用方便、快速反应能力强等突出优点,成为各类主动攻击型深海武器的首选动力。发动机在水下工作时,由于外部水介质的密度大、环境压强高等特点,使其工作过程变得极为复杂[1]。例如,发动机点火后,水环境的惯性作用严重制约喷管内气体的喷出,可能使发动机工作故障或失败;高速燃气射流与周围水环境之间的相互作用,导致推力难以预估;深水情况下推力和阻力存在耦合关系,使得深水工作推进系统的实际推力与理论计算值相差较大;深水发动机推力损失异常,难以用简单的背压变化机理解释等。因此,深入了解水下发动机推力特性,具有十分重要的理论意义和工程应用价值。
在早期研究中,Rogers[2]提出了球形气泡模型,并运用该模型对水下发动机点火瞬间产生的最大推力进行了预测。Labotz[3]在球形气泡模型的基础上,对发动机水下点火后达到平衡压强的最短时间进行了估计。Tang[4]等将球形气泡模型的计算结果与CFD计算结果进行对比,发现球形气泡模型结构简单,计算速度快,并能有效反映发动机点火瞬间的推力峰值特性。但由于该模型假设气体在整个射流过程中以单一气泡结构存在,并沿径向等速无限膨胀,因此不能用于说明较长时间内的压强及推力特性。Lindau[5]等对考虑空泡作用下的高速超空化水下推进过程进行了数值研究,提出了包括燃气、水和水蒸气的三相流计算模型,但没有对水下推进过程中的流动特性和发动机工作性能做进一步分析。
Tang等[6]建立了水下超音速气体射流数学模型,并将数值计算结果与实验结果进行对比,验证了该模型的合理性和准确性,为水下固体火箭发动机工作过程的研究提供了基础。该水下超音速气体射流数学模型中采用固定压力入口边界条件,即喷管入口处的总压从工作开始到结束都保持恒定,不会受到下游流场的影响。然而,在实际的水下发动机工作过程中,一方面存在燃烧室建压延迟过程;另一方面,外部水环境高压可能对燃烧室内工作情况产生影响。因此,喷管入口处的总压并不能保持恒定。例如,外部水介质在点火瞬间产生的惯性作用会对喷管内流动产生阻滞,使燃烧室内部压强升高;高速燃气与水体发生强烈撞击后产生的强激波可能反传入喷管内,使上游燃烧室压强发生振荡,从而导致固体推进剂燃速和燃气生成率发生变化。当发动机所处水深较大、外部水环境压强较高时,此影响更为严重。因此,Tang等[6]提出的水下超音速气体射流数学模型,适用于喷管喉部达到音速流或不考虑发动机点火初期工作特性的情况。
为准确模拟水下固体火箭发动机工作过程,并深入分析点火初期的工作特性,本文将在Tang等[6]提出的水下超音速气体射流数学模型的基础上,结合固体推进剂的燃烧特性,对燃烧室内固体推进剂燃气质量生成过程和水下超音速气体射流过程进行耦合求解。
1 建模与计算方法
1.1 控制方程
在水下固体火箭发动机的工作过程中,将气体视为目标流体,基于Volume of Fluid(VOF)多相流模型的质量、动量、能量守恒方程及体积分数输运方程分别为

其中,φm为混合相的物理性质,由 φm=φgαg+φw(1-αg)计算得到,φ可用来表示密度、粘性系数等物理量;下标w表示水,g表示气体。气液两相的体积分数关系为αw+αg=1。模型中,将气体假设为理想气体,水为不可压缩相。由于水下气体射流过程中的Froude数约为0(103),因此在动量守恒方程(2)中,可忽略体积力Fi的作用。在能量方程(3)中,Sh为源项;keff为有效热传导率(k+kt),其中kt是湍流热传导率,根据所采用的湍流模型定义;能量Ek可由下式决定:

在本文的研究中,假设火箭发动机固定不动,整个射流过程属于高压范畴,不考虑由于超低压作用产生的空泡现象,且不考虑气-液相之间的相变作用。因此,体积分数输运方程(4)右端项为0。
1.2 湍流模型
选用标准k-ε湍流模型,对雷诺平均N-S方程进行封闭。该湍流模型适合完全湍流流动,是针对高雷诺数的湍流计算模型。湍流动能k及湍流能量耗散率ε由以式(6)及式(7)求得:
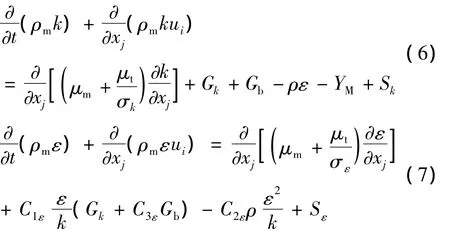
式中Gk和Gb分别表示由时均速度梯度和浮力产生的湍流动能;YM体现了流体可压缩性,定义为YM=,其中Mt=(k/ γRT)1/2为湍流马赫数;Sk和Sε是用户定义的源项。
由于不考虑体积力作用,且流场中无源项存在,所以Gb、Sk和Sε均为0。湍流粘性系数定义为

其中,C1ε、C2ε、Cμ、σk和 σε均为常数,取值如表 1 所示。

表1 湍流模型中的常值参数Table 1 Constant parameters of the turbulence model
1.3 计算域及边界条件
采用二维轴对称模型,对水下固体火箭发动机工作过程进行计算。计算域包括喷管内流动区域和喷管外射流区域。计算域如图1所示,总长度为喷管出口直径的600倍,宽度为喷管出口直径的35倍,以克服边界条件对主射流区流动的影响。计算中,将整个计算区域分解为多个区域,并对各个区域分别生成计算网格。同时,根据流动物理特征分析,在壁面、喷管喉部及射流核心区等物理量变化梯度较大区域进行网格加密。

图1 轴对称计算域及水下发动机结构Fig.1 The axis-symmetric computational domain together with the geometry of the underwater engine
由于在水下发动机的工作过程中,固体推进剂燃速会影响发动机燃烧室压强的变化过程;同时,燃烧室压强又将反过来影响推进剂燃速,引起喷管质量流量和下游气-液两相流场的变化。因此,为了结合固体推进剂的燃烧特性,研究中借助用户自定义函数(UDF),使用C语言编写扩展FLUENT的程序代码,然后动态加载到FLUENT环境中,对喷管入口边界条件进行定义。喷管入口处采用质量入口边界条件,入口质量流量为

式中表示喷管入口处气体的质量流量为固体推进剂燃气质量生成率,由推进剂燃烧特性和燃烧室压强共同决定;为固体推进剂燃速;表示入口处水的质量流量,因为入口处介质为燃气,所以=0;燃烧室压强pc会受到发动机外部气-液两相流场的影响,并不保持恒定。
在自由出口边界上,总压等于环境压强,由喷管所处的水深决定;总温等于水环境的温度,假设为300 K。壁面采用固壁面边界条件,无滑移且绝热;流场中心采用轴对称边界条件。
初始时刻,喷管内为气相区,喷管外为水环境区,两个区域均处于静止状态。喷管入口处的初始压强等于实验中给定的发动机燃烧室初始压强pinitial,水环境区域的初始压强等于实验中发动机所处水深处的环境压强ρwgh+p1。其中,h为水深;p1为大气压强,取值等于0.101 MPa。计算开始时,喷管内外2个区域瞬间联通,流动建立。
1.4 耦合求解过程
耦合求解过程如图2所示。首先,用给定的发动机燃烧室初始压强进行初始化,开始第一步迭代计算,燃烧室入口边界处的燃气质量流量根据初始压强下的推进剂燃速计算得到;然后,对分离求解后得到的计算结果进行判断,若计算不收敛,则继续迭代,若计算收敛,则本次循环终止;同时,运用UDF读取本次循环结束后得到的燃烧室入口边界处的压强值,并根据新读取的压强值计算得到新的燃气生成率,将其作为下一步迭代计算的入口质量流量值,开始下一次迭代,计算时间步长Δt=10-6s。本文研究中,采用有限体积法对控制方程进行离散,并运用SIMPLE算法对流场进行求解。考虑到气-液两相流数值计算量大的特点,选用一阶迎风格式进行插值。
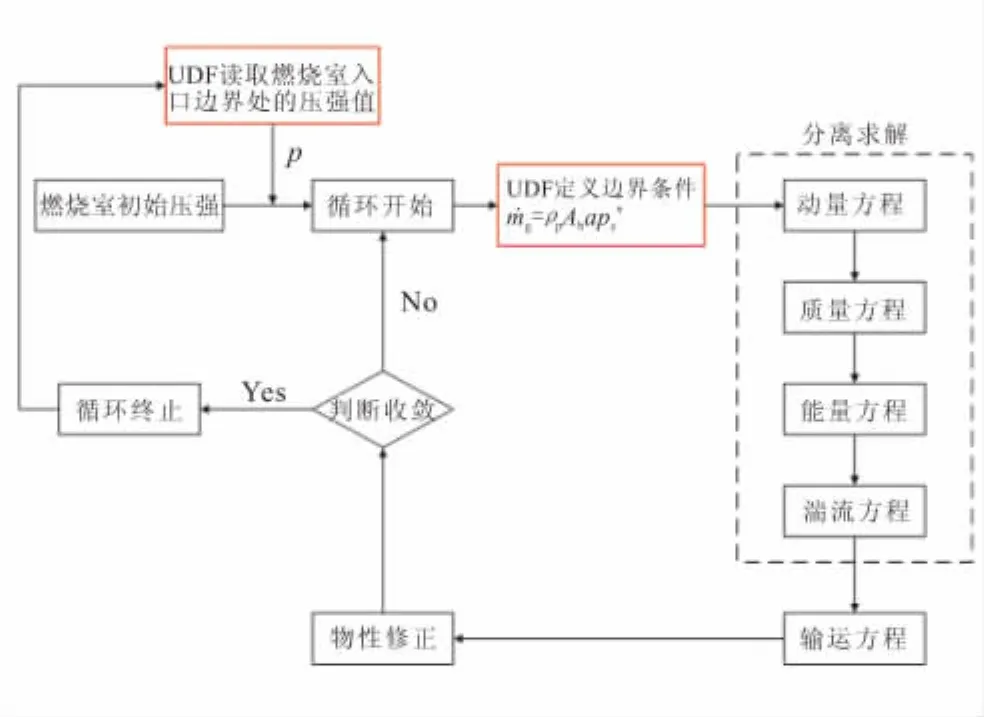
图2 燃气质量生成与水下超音速气体射流的耦合求解流程Fig.2 The coupling simulation method between the process of gas generation and the process of gaseous jets injected into water
1.5 推力计算方法
火箭发动机在水下工作时,由于高速燃气与水之间的相互作用以及射流过程中的膨胀、胀鼓、颈缩/断裂和回击现象的出现,整个工作过程为非稳态的湍流过程[6]。另一方面,发动机外壁所受到的外部介质的静压作用非均匀分布,且发动机尾部所受到的背压不等于环境压强,pa≠pB。因此,水下火箭发动机的推力不可按空气中的简化推力公式[7]来计算。根据图3所示,对发动机内外表面所受到的压力进行积分,可得水下发动机推力计算公式为
式中re、rs分别表示喷管出口和发动机外壁所对应的半径。
由式(9)可知,水下火箭发动机推力由3部分组成:第一部分为动量推力,由高速燃气产生的动量变化率提供;第二部分为压力推力,由喷管出口截面上的压强pe与外界环境压强pa之间的压差产生;第三部分为压力推力,由作用于发动机前后端面上环境压强pa与背压pB之间压力差产生。

图3 发动机推力计算方法示意图Fig.3 Computation schematic of the rocket engine thrust and pressure distribution
2 计算结果及分析
在本文的计算中,选取的装药为端燃药柱,燃面Ab在燃烧过程中保持不变。推进剂燃速为r==cm/s(pc单位为 kg/cm2),推进剂密度ρP=1.5×103kg/m3。不同的燃烧室平衡压强可通过调整装药燃烧面积来实现。发动机尺寸和详细工作参数如表2所示。其中,dt、de、ds分别表示喷管喉部、出口及发动机外壁所对应的直径;Ae/At为喷管扩张比。

表2 发动机结构及工作条件Table 2 The geometries and operation conditions of the simulated engine
2.1 计算结果与实验对比
运用本文建立的燃气质量生成与水下超音速气体射流的耦合计算模型,对表2中的H-5型发动机工作过程进行模拟,得到推力-时间曲线如图4(a)所示。实验测量得到的推力-时间曲线如图4(b)所示。图4(a)和(b)中,纵坐标为无量纲化后的推力F/Fref,无量纲参数Fref为发动机燃烧室压强达到平衡后的平均推力。比较两图可知,水下发动机在点火初期会出现推力峰值,峰值后均出现了负推力现象,之后推力缓慢爬升达到平衡,在整个过程中伴随有强烈的推力振荡。推力爬升是建压过程中燃烧室压强不断升高引起的,推力振荡是水下超音速气体射流过程中膨胀、胀鼓、颈缩/断裂和回击现象[6]循环出现的结果。通过耦合计算方法得到的发动机推力在开始瞬间为负值,如图4(a)所示,而通过实验方法测量得到的推力在开始瞬间为0,如图4(b)所示。这是由于实验中的发动机喷管出口处装有尾盖,只有当尾盖左侧(喷管内)的压强比尾盖右侧(喷管外)的压强高出一定值时,尾盖才会被吹开,以防止外部流体倒流,因此实验中的发动机推力在开始瞬间为0。耦合计算过程中,没有考虑喷管尾盖的影响,即计算开始时,喷管内外的两个区域瞬间联通。因此,在外部环境压强较高的情况下,喷管出口处的流体会在初始瞬间出现倒流现象,使推力在初始瞬间为负值。由图4(a)和(b)可知,通过耦合计算方法和实验方法得到的推力-时间曲线变化趋势吻合较好,说明了本文提出的耦合计算模型的合理性。

图4 水下固体火箭发动机推力随时间的变化曲线Fig.4 Time vs thrust profile of the underwater solid rocket engine
图5(a)为通过耦合计算方法得到的H-5型发动机喷管内的压强-时间变化曲线,测压点位于喷管扩张段内距离喷管出口0.1 m处。图5(b)为通过实验方法测量得到的压强-时间曲线。两图中,纵坐标为无量纲化后的压强p/pref,参考压强pref为发动机燃烧室压强达到平衡后测压点处的平均压强值。比较两图可知,在发动机点火初期,喷管扩张段内会出现很高的压强峰值,压强从峰值回落后将出现短期振荡,然后缓慢爬升至平衡值。压强峰出现的原因为发动机点火初期,大量燃气冲出喷管与水发生撞击,在水环境的静压和惯性作用的影响下,喷管扩张段内产生了反传压力波,当压力波到达测压点时,便会引起压力峰值的出现。发动机水下点火过程中出现在喷管内的压强峰是水下工作的特别现象,相同发动机在地面实验中,并没有观察到该现象。实验测量得到的压强在爬升之后,还会出现轻微振荡(如图5(b)所示),主要原因是当喷管扩张段内压强较低、环境压强较高,或测压点离喷管口较近时,测压点工作情况容易受到外部气-液两相流动的影响,使喷管内压力出现波动。由图5(a)和(b)可知,通过耦合计算方法和实验方法得到喷管扩张段内的压强-时间曲线变化趋势吻合较好,说明了本文提出的耦合计算模型合理性。

图5 水下固体火箭发动机喷管内压强随时间的变化曲线Fig.5 Time vs pressure profile tested in the nozzle of the underwater solid rocket engine
2.2 负推力现象及其产生的原因
基于本文的数值模拟结果,对发动机点火初期的负推力现象进行深入研究。由图4(a)可知,发动机点火初期首先出现较高的推力峰值,对应工作时间为0.015 s。峰值之后,推力迅速降低到负值,出现负推力现象,对应时间为0.022 s。为了分析负推力现象出现的原因,图6和图7中分别给出了工作时间为0.015 s(推力峰值出现时刻)和0.022 s(负推力出现时刻)时的流场液体体积分数云图和压强分布云图。首先,从图6(b)中可知,当工作时间t=0.015 s时,燃烧室产生的高速燃气与惯性作用很强的水发生强烈撞击,在喷管尾部产生一个高压区。此时,喷管出口压强和背压都急剧升高,从而导致推力峰值的出现,如图4(a)所示。由于此时燃烧室压强尚未达到平衡压强值,喷管内部压强较低,外部环境高压会把周围的水介质反推入喷管内,使喷管内流动受阻并达不到超音速流动,如图6(a)所示。

图6 H-5型水下发动机在t=0.015 s时的流场结构云图Fig.6 Flow structures of engine H-5 in the water at t=0.015 s

图7 H-5型水下发动机在t=0.022 s时的流场结构云图Fig.7 Flow structures of engine H-5 in the water at t=0.022 s
随着燃烧室压强的升高,以及外部水流场流动的建立,喷管内流动受到的阻碍逐渐减弱,燃气在被过度压缩之后,进行快速膨胀,喷管中的超音速气流终于冲出喷管口,并在喷管尾部形成一个超音速燃气泡,如图7(a)所示。燃气泡内的超音速流动,使泡内压强降得很低,在流动惯性作用的影响下,气泡将持续膨胀,使泡内压强进一步降低,并低于环境压强,如图7(b)所示。

3 结论
(1)建立了固体推进剂燃气质量生成与水下超音速气体射流流动的耦合计算模型,通过与水下固体火箭发动机的实验数据对比,验证了模型的合理性。模型可反映出水下发动机外部气-液两相流场对燃烧室压强和推进剂燃速的影响,为深水发动机的研究提供了基础。
(2)水下发动机在点火初期会出现推力爬升和负推力现象,推力爬升是建压过程中燃烧室压强不断升高引起的。
(3)水下发动机点火初期产生负推力现象的原因是发动机点火初期,喷管内被过度压缩的燃气冲出喷管后,在喷管尾部形成一个超音速燃气泡,超音速流动使泡内压强降低;同时,由于受到流动惯性作用的影响,气泡持续膨胀使泡内压强进一步大幅降低,从而导致发动机产生的推力变为吸力,产生负推力现象。
[1]张有为,王晓宏.导弹水下点火推力峰值问题的数值研究[J].应用力学学报,2007,24(1):298-301.
[2]Rogers K W.A theoretical and experimental investigation of the transient phase of underwater rocket motor firing[R].U-niversity of Southern California Engineering Center Report,1962.
[3]Labotz R J.Hydrodynamic consideration and limitations in submerged rocket firings[J].Journal of Spacecraft and Rocket,1965,2(3):320-324.
[4]Tang J N,Li S P,Wang N F,et al.Flow structures of gaseous jet injected into liquid for underwater propulsion[C]//46th AIAA/ASME/SAE/ASEE Joint Propulsion Conference and Exhibit,Nashville,TN.2010,AIAA 2010-6911.
[5]Lindau J W,Venkateswaran S,Kunz R F,et al.Multiphase computations for underwater propulsive flows[C]//16th AIAA Computational Fluid Dynamics Conference,Orlando,Florida,AIAA 2003-4105.
[6]Tang Jia-ning,Wang Ning-fei,Wei Shyy.Flow structures of gaseous jets injected into water for underwater propulsion[J].Acta Mechanica Sinica,2011,27(4):461-472.
[7]董师颜,张兆良.固体火箭发动机原理[M].北京:北京理工大学出版社,1996.
Study on the negative thrust of the underwater solid rocket engines
TANG Jia-ning,LI Shi-peng,WANG Ning-fei
(School of Aerospace Engineering,Beijing Institute of Technology,Beijing 100081,China)
To simulate the working process of the underwater solid rocket engines,a coupling model between the process of gas generation and the process of gaseous jets injected into water was proposed.The burning rate of the solid propellant was considered in this coupling model and the User Defined Functions(UDF)were used to define the boundary condition of the nozzle inlet.The numerical method is validated by the experimental data.The results show that the negative thrust appears when the engines work in the water.The reason is as follows:at the initial stage of the propulsion process,the high compressed gas jets into water to form a supersonic“gas bag”behind the nozzle exit,causing the pressure in this area to drop suddenly.Furthermore,the inertia effect of the water causes the pressure in the“gas bag”to keep dropping,creating the negative thrust due to the pressure difference between the rear and front parts of the engine.
underwater solid rocket engine;thrust;submerged gaseous jets;multiphase flow
V435
A
1006-2793(2012)03-0325-05
2011-11-09;
2011-12-01。
唐嘉宁(1984—),女,博士生,研究方向为水下固体火箭发动机。E-mail:tjn1216@163.com
(编辑:崔贤彬)
