多阈值选取与边缘连接的边缘检测算法

朱晓临， 邓祥龙， 胡德敏

（合肥工业大学数学学院，安徽 合肥 230009）

图像是人眼最直接接收到的事物的最原始的信息，图像中最重要的信息是由图像中边缘和轮廓提供的，所以对图像中目标物体边缘的研究是非常必要的。在医学图像处理中，边缘检测是非常关键的技术之一，目的是更好地将目标物体的边缘标记出来。例如在肿瘤病灶确定、椎间盘边缘位置确定、冠心病诊断、左心室边缘抽取、脑腔血块大小检测等方面占有举足轻重的地位。

在图像处理中，边缘是指图像中其周围像素灰度值有阶跳性变化和屋顶状（灰度值由增加到减少的变化转折点）变化的那些像素的集合。因为图像采集过程中存在一些不确定的因素，干扰了图像的清晰度，会产生噪声、对比度不强、图像模糊等等问题，从而影响对图像关键信息——边缘的提取或强化，所以人们一直致力于研究和解决如何构造具有良好性质和检测效果的边缘检测方法。现阶段比较成熟的是传统的图像边缘检测方法，微分运算是传统边缘检测与提取的主要手段。根据边缘具有阶跳性变化或屋顶状变化的特点，边缘点对应于图像中一阶微分最大或最小、或是二阶微分呈零交叉或二阶微分取极值的点。一阶微分算子包括 Robert算子[1]、Sobel算子、Prewitt算子[2]和 Kirsch[3]算子等，二阶微分算子包括Laplacian算子、LOG[4]算子等。另外，Canny[5]算法是种基于一阶微分的多尺度边缘检测算法，是一种较好的边缘检测算法，但为了得到较好的边缘检测结果，通常需要使用较大的滤波尺度，这样容易丢失一些细节。

上述边缘检测算子中，Kirsch算子在医学图像边缘检测以及其它很多领域都一直在广泛应用，例如Li Huiqi, Opas chutatape在2000年提出利用 Kirsch算子检测糖尿病性视网膜病变后眼底图像的边缘来区别不同成分[6]；M A Bottalico,A Starita在2000年利用Kirsch算子检测颈动脉超声图像边缘[7]；Mahmoudi, Maryam Tayefeh在2003年研究了它在车道检测中的应用[8]，在嘈杂的环境中 Kirsch算子有较好的检测效果；Md Saidur Rahman[9]等在2009年利用Kirsch算子对手写数字进行识别；高萍、王伟等在 2010年将它与光流法结合检测运动物体[10]等。Kirsch算子采用8个模板进行检测，能较好地保持图像的细节，但存在着计算量大、检测运行时间长、边缘连接性较差、丢失弱边缘等缺点。针对Kirsch算子存在的缺点，近些年来国内外学者对其进行了进一步研究，例如吕俊白在 2001年通过矩阵变换来减少算子的运算量[11]、吴怀宇在 2009年采用改进的Otsu法[12]和王宝树在2009年采用抛物线法[13]自动获取阈值来保持图像弱边缘，但仍存在弱边缘提取不全的缺点。

本文采用一种多阈值选取和边缘连接算法对 Kirsch算法进行了改进，可以获得保持弱边缘、连接性较好的检测结果。

1 传统Kirsch边缘检测算子

Kirsch算子是几种经典的边缘检测算子之一，至今仍有广泛的应用。1971年，R. Kirsch[3]提出了一种图像像素顺时针循环求梯度的方法来进行边缘检测。他使用8个模板来确定梯度的大小和方向，是一种最佳匹配的边缘检测。

设待检测图像的3×3子图像如下：

0 a a1a27 a (i, j) a36 a a5a4

用 M0～M7分别与子图像中的各个对应元素相乘，计算这8个结果的最大值作为中心像素的近似梯度值，其对应的方向作为边缘的方向；8个卷积核形成了Kirsch算子。在进行边缘提取时，图像中每一个像素对应的3×3子图像都与这8个模板进行卷积，然后输出最大值。

Kirsch算子通过对图像进行8个方向的边缘检测能取得较好的效果，它可以较好地保持图像的细节，但是最初得到的边缘图像较为粗糙，一般采用取阈值的办法来获得较为清晰的边缘图像。而这样得到的边缘图像，经过人工取阈值以后，容易产生连续性较差的问题，同时容易丢失掉梯度值较小的弱边缘。

2 多阈值选取与边缘连接的边缘检测算法概述

设I表示待检测图像，I( i, j)表示图像I中(i, j)处的像素值。用上述8个模板对待检测图像I做卷积，则式(1)表示8个模板对图像I做卷积所得到的(i, j)处的梯度值。可以由一系列m( i, j)组成梯度图像G

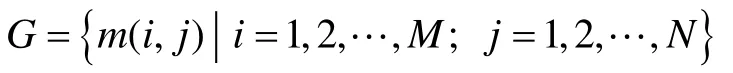
其中，M和N表示待检测图像I的高度和宽度。

传统的Kirsch算子在获得了梯度图像G以后，设定了一个阈值，然后对图像进行二值化，得到最后的边缘图像。这时，若阈值选取过大，则可以去除虚假边缘，但同时也造成了弱边缘的丢失；若阈值选取过小，则可以保持弱边缘，但又会造成虚假边缘增多。因此固定地选取某一个阈值总是不能很好地解决二者的矛盾。

针对Kirsch算子的缺点，本文提出多阈值选取与边缘连接的边缘检测算法：为了避免噪声对边缘检测的影响以及检测出虚假边缘，首先对原始图像用Gauss滤波进行去噪处理，然后利用传统的Kirsch算子提取图像边缘，再设定一个较低的阈值保持图像的全部边缘、一个较高的阈值提取出图像真正的边缘，得到连接性较差的边缘图像，再利用局部均值与标准差获得一幅边缘连接完整但粗糙的图像作为下一步边缘连接的基础，最后利用本文改进的边缘连接算法将断裂的边缘连接，从而得到连接性良好的边缘图像。

3 算法具体步骤

根据以上分析，本文算法分4步进行，具体步骤如下：

Step 1 在进行传统的 Kirsch算子处理之前，我们首先采用较小尺度的Gauss滤波对图像进行平滑去噪，目的是消除噪声对边缘检测的影响以及去除噪声点等虚假边缘。设二维Gauss函数[14]为

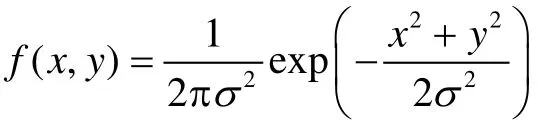
σ为Gauss函数标准差。对图像用Gauss滤波做平滑去噪实质上是将图像与Gauss函数做卷积的过程。我们这里选择Gauss核为3，σ2=1的Gauss滤波器对图像进行处理，这样可以在去除噪声点的同时更好地保留了边缘效果。

Step 2 利用传统的Kirsch算子进行边缘检测，得到上述梯度图像G。

Step 3 设定一个低阈值，记为T1，它的选取原则是不造成弱边缘的丢失，即T1小于弱边缘点对应的梯度值。这样我们得到包含我们想要的全部边缘的图像D

图像D的边缘点的梯度值大于T1，这会造成图像D的边缘线较为粗糙，模糊不清。如果我们想得到较为细腻、清晰的边缘线，一种最直接的方法就是在图像D的基础上再设定一个较大的阈值，即大于这个较大的阈值的边缘点都被认作为图像的边缘。但这样做的结果是边缘线不连续，因为只有部分符合条件的边缘点被保留了下来。

本文的做法是利用局部图像的像素值的均值和标准差，自适应地选取较大的阈值。

对图像D求每个3×3子图像像素的标准差。以(i, j)为中心的3×3子图像的像素标准差为

由表达式可知，图像F1是由图像D中局部区域 D ( i, j)≥T2的点所构成的，这些点一定是图像的边缘，而在 D ( i, j)＜T2的点中也会含有一些图像的边缘，于是这样的取值可找到图像的部分真正边缘，但是图像F1中的边缘是断裂的，连接性差。

因此，我们再取T3＞D( i, j)，得到图像D中像素值大于其局部平均值的点的集合F2

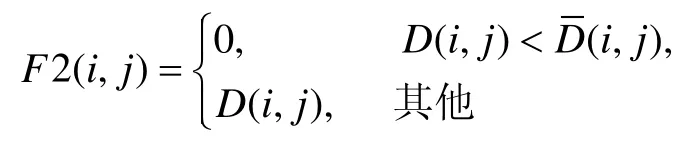
作为对下一步连接边缘图像的基础。

Step 4 通过以上的方法，我们得到了一个初步的边缘图像结果，图像中还存在一些断裂的边缘线。为了得到更好的边缘图像，我们采用一种基于“边缘模式”的连接算法[15]来得到连续边缘。

在3×3子图像中，边缘的存在形式有16种，如图1所示。

图1 3×3邻域16种边缘模式

图1中黑色部分表示图像边缘。

连接边缘的具体做法是：

Step 4.1 逐一扫描边缘图像F1的每一个像素。若(i, j)是边缘像素，则在图像F2中找到与(i, j)对应像素的3×3子图像SFi,j，在这个3×3子图像上定义上述16种边缘模式。

Step 4.2 设 E MVn表示SFi,j中第n种边缘模式对应的3个像素之和

Step 4.4 用M1,,表示 3×3子图像中对应于模式中的像素。给定阈值，如果＞T4，那么在3×3子图像中与，，有相同位置的像素被标记为边缘像素，令其像素值为255；否则不是边缘像素。

其中阈值T4的取法：文献[15]中该阈值取为2.5382～10.153之间，这会造成图像边缘连接不完全以及连接的边缘在两端处出现“工”字型边角。本文取

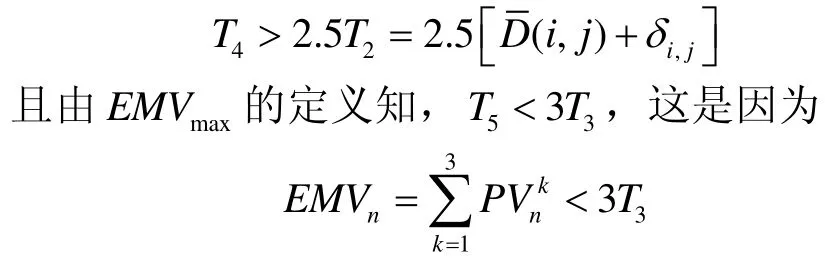
Step 4.5 重复上述步骤，直至图像没有新的边缘点增加。

利用上述边缘连接算法可以得到连续性良好的边缘图像，连接后的图像会出现许多孤立的噪声点，去除孤立点的方法为：在连接完毕的边缘图像中，逐一检查3×3子图像，计算子图像的像素之和，若和为255，则认为是孤立点，将其去除。

4 算法的实现和结果比较

下面分别用不同阈值下的传统Kirsch算子、本文的多阈值选取与边缘连接的边缘检测算法对Lena标准图像进行边缘检测，检测结果如图2所示。

图2 不同阈值的Kirsch算子与本文方法的Lena图像检测结果

图2中的(a)为 Lena原图，(b)、(c)、(d)为Kirsch算子阈值分别取 20、30、40后的边缘提取结果，(e)为本文方法提取结果。由图2可见，当Kirsch算子选取较低阈值时，可基本将图像边缘提取出来，但轮廓线粗糙模糊；随着加大阈值，虽轮廓线稍加清晰，但造成了较为严重的边缘丢失。而本文方法可以在清晰轮廓的同时较好地保持边缘。

目前，Canny算子是最常用的边缘检测方法。下面用传统的Kirsch算子、Canny算子和本文方法对人体大脑、胸腔、腹腔的CT图像进行边缘检测，检测结果如图3所示。

图3 中的(a1)、(a2)、(a3)为原图，(b1)、(b2)、(b3)为传统Kirsch算子检测结果图，(c1)、(c2)、(c3)为Canny方法检测结果图，(d1)、(d2)、(d3)为本文算法检测结果图。通过实验结果对比可知，Kirsch算子能一定程度地检测出图像边缘，但是边缘提取粗糙，丢失边缘严重；Canny算子能较好地提取出边缘，但对图像的弱边缘检测不全。仔细观察图像(d1)、(d2)、(d3)与对应的原图，(d1)、(d2)、(d3)中的细小的短边并不是多余的噪声，而是Kirsch算子与Canny算子没有检测出的图像弱边缘，因为算法中设定的低阈值T1保持了图像的弱边缘。结果显示本文的算法能有效地保持图像弱边缘，且边缘轮廓比较清晰。

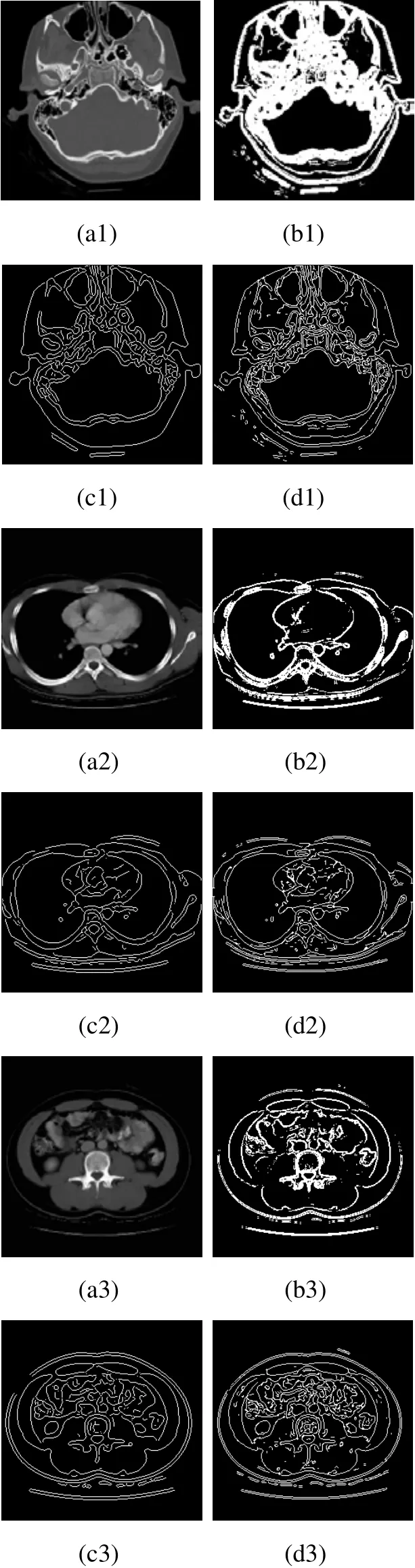
图3 Kirsch算子、Canny算子与本文方法的检测结果

5 结 论

针对Kirsch算子的缺点，本文提出多阈值选取与边缘连接的边缘检测算法：首先对原始图像用 Gauss滤波进行去噪处理；再利用传统的Kirsch算子提取图像边缘：先设置一个低阈值，保证检测到图像的所有弱边缘；然后利用均值和标准差来自适应设定高阈值，提取出图像各个部分的真正边缘；最后利用本文改进的边缘连接算法连接边缘，从而得到连接性良好的边缘图像。试验表明，本文的边缘检测算法能够保持图像的弱边缘，很好地连接断裂的边缘线，检测出的边缘细腻光滑，噪声点较少。

[1]Roberts L G. Machine perception of three-dimensional solids [D]. Massachusetts: MIT Press, 1963.

[2]Prewitt J M S. Object enhancement and extraction [C]//Picture Processing and Psychopictorics. Academic Press, New York. 1970: 75-149.

[3]Kirsch R. Computer determination of the constituent structure of biological images [J]. Computers and Biological Research, 1971, 4(3): 315-328.

[4]Marr D, Hildreth E C. Theory of edge detection [C]//Proceedings of the Royal Society of London. Series B,Biological Sciences, 1980, 207(1167): 187-217.

[5]Canny J. A computational approach to edge detection [J].IEEE Trans. Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6): 679- 698.

[6]Li Huiqi, Opas C. Fundus image features extraction [C]//Proceedings of 22th Annual EMBS International Conference, 2000, (4): 3071-3073.

[7]Bottalico M A, Starita A. A computer tool to support carotid ultrasound images analysis [C]//Proceedings of 22th Annual EMBS International Conference, 2000,(4): 2428-2430.

[8]Mahmoudi, Tayefeh M. A comparative study of edge detectors for lane detection [C]//Proceedings of the International Conference on Imaging Science, Systems and Technology, 2003, (2): 526-530.

[9]Rahman M S. An approach to recognize handwritten Bengali numerals for postal automation [C]//Proceedings of 11th International Conference on Computer and Information Technology, 2008: 171–176.

[10]Gao Ping, Sun Xiangju, Wang Wei. Moving object detection based on Kirsch operator combined with Optical Flow [C]//Image Analysis and Signal Processing (IASP), 2010: 620-624.

[11]吕俊白. 基于快速Kirsch与边缘点概率分析的边缘提取[J]. 计算机应用, 2001, 21(2): 33-35.

[12]薛孝琴, 吴怀宇, 游辉胜. 一种改进 Ostu法在Kirsch边缘检测中的应用[J]. 计算机与数字工程,2009, 37(3): 167-171.

[13]康 牧, 王宝树. 自适应 Kirsch边缘检测算法[J].华中科技大学学报, 2009, 37(4): 47-50.

[14]阮秋琦. 数字图像处理基础[M]. 北京: 清华大学出版社, 2009: 155-156.

[15]张光玉, 龚光珍, 朱维乐. 基于克隆算法的彩色图像边缘检测新算法[J]. 电子学报, 2006, 34(4):702-707.