一类新疆民族风格的织物图案生成方法

赵海英 ， 徐正光， 张彩明

（1. 北京科技大学自动化学院，北京 100083；2. 新疆师范大学计算机科学技术学院，新疆 乌鲁木齐 830054；3. 山东大学计算机科学与技术学院，山东 济南 250101）

新疆民族织物图案是中华民族文化宝库中的艺术瑰宝，具有重要西部人文风格特点。随着计算机辅助设计的发展，如何利用计算机辅助设计加快图案的制作速度、丰富了图案的设计创作形式是 CAD的一个重要课题[1]。当前大量的拷贝、裁剪、粘贴等简单、重要、没有创造力的劳动[2]，是制约中国纺织产业进一步发展的难题。面对现代化和国际化的发展变化，传统民族服饰作为历史的产物，即使是最优秀的部分难以适应现代社会的审美及实用需要，必须会随着历史的流失而消亡。因此，必须运用现代设计理念和方法对其进行改造创新，使之成为既有民族地域特色又具有时代风格的新的织物图案。论文引入纹样基因的概念是为设计具有民族特色的现代织物图案奠定基础，并作为纹样设计中可以使用的、有代表性的元素。力求设计时既古为今用，又兼具民族特色。

论文研究新疆民族织物图案的计算机自动分割就在于能够发现和提取具有民族风格的纹样基因，并以此生成出符合新疆民族特色的图案。

1 相关工作

纺织CAD 从图案花型设计到实用等各个环节都实现了自动化，但图案花型的设计，还更多依赖于设计者。如何基于数学理论和各类工具自动生成纹样图案，是研究者关注的重点。目前，前人已提出许多行之有效的方法，尤其在织物风格、几何造型和植物模拟方面，研究成果显著。如分形模型的字符重写系统(String Rewriting System)[3]、迭代函数系统(Iteration Function System)[4]、复数平面分形系统(Complex Plane Fractal System)[5]、元胞自动机(Cellular Automata)[6]、有限扩散凝聚模型(Diffusion Limited Aggregation[7]) 等一系列生成图形方法，这些方法不仅具有生成图形分形化，而且通常可用迭代方法实现，使复杂景物使用简单规则生成，生成的纹样图案也是人们意想不到的，这极大地丰富纺织品的花色品种，缩短花型设计的周期。如丹麦植物学家A Lindenmayer在 1968 年创造性地提出了一个植物形态学模型，简称为L 系统[8]，有人[9]提出了一种基于剪纸纹样库进行计算机辅助生成剪纸形象的方法。另外，徐迎庆等研究者提出了剪纸模型[10]，实现了一类新的设计创新形式。不同方法以不同的方式对对民间艺术进行数字化，但是这些图案的生成方法大多从物理特性出发的，更多考虑的是视觉效果而不是基于图案本身语义层面的设计。本文对织物图案的设计也追求美观的视觉效果，但更重视的是要能传承和保留新疆风格与特色，论文提出分割纹样基因生成织物图案的方法。

图案分割准则不是唯一的，将织物图案分割成一些具有某种一致性的区域，这个一致性包括亮度、颜色或纹理等衡量标准。但织物图案（如图1）多包含蜿蜒的曲线、规则与不规则的几何图形、对称与不对称的图案纹样，一般没有明显的纹理基元，也无明显的周期性和方向性，但是它往往包含有丰富的曲线细节，有的还具有随机变化的形状。因此，对其分割难度很大，基本没有统一的标准。本文以设计具有民族风格的图案为需求，提出特征过滤图案基元提取纹样基因算法，通过对分割区域进行特征比对过滤重复、较小、无意义图案元素，提取具有应用价值的设计元素应用于图案生成中，传承民族风格设计。

图1 维吾尔族花帽图案及纹样基因

2 纹样基因

民族织物图案蕴藏着丰富的传统文化，对民族图案的研究除了建立模型外，还需要建立艺术基因库来保护和传承民族文化。新疆维、哈、柯等民族织物图案的存在是一笔极其宝贵的文化财富，不仅对新疆未来的文化艺术，甚至对于中华民族未来的文化艺术，都有不可估量的再生和再创造价值。分析新疆民族织物图案特点，挖掘、解码图案内在本源，引入基因工程方法。在生物学中，基因是一个功能单位，基因不仅可以通过复制把遗传信息传递给下一代，还可以使遗传信息得到表达。借用生物学的基因词汇，给出纹样基因的定义：

定义：基因是在特定地域和民族文化环境中形成的、具有稳定性和继承性的基本信息模式，它反映了独特的风格，具有可量化、可计算、可分析的特点。

我们将通过纹样基因的研究揭示民族织物的风格特征。一幅图案是由不同纹样基因组成，它不是基因的简单聚合体，而是更高语义层次的单位整合。从表面上看，图案本身只是一个和谐的组合体，其实它更是人类民族文化的载体，反映着历史的内容，也对这个历史起着决定因素。对维、哈、柯民间织物图案研究，是要把民族文化研究与历史研究有机结合起来，这种研究就必然蕴含着一种结构观念、历史观念、系统观念。借助生物基因的研究方法，一是要忠实原风格地复制图案基因，保持织物图案的本质特征；二是要基因能够“变异”， 选择其一小部分“变异”或“重组”，给民间织物图案的创作输送创新性的原始材料，使图案成为设计中最适合民族风格的基因个体。

本文研究的纹样基因除具有稳定性、继承性、典型性特征外，还具有单一色彩、最小构图结构的特点。通过分析这些特点，利用连通区域标记算法进行分割，最终以特征过滤筛选出设计纹样基因。

3 基于纹样基因的图案生成算法

本文通过特征筛选过滤图案基元提取纹样基因；进而分析民族织物图案进行特点，发现其基本元素具有对称排列特征，以设计六边形构型为主可实现对称民族织物图案生成。

3.1 纹样基因提取方法

纹样基因提取由连通区域标记、图案基元切割、提取基元特征、设计特征筛选规则过滤基元四部分组成。

3.1.1 图案连通区域标记

图案连通区域标记是获取纹样基因最关键也是最重要的一步，整个过程由图像尺度放大、图像二值化、膨胀和开运算以及块状区域连通标记4个过程展开。

1）图案尺度放大

首先，通过双线性内插值算法对输入图像尺度放大，有利于连通区域的后期断线缝合获取。对于较小尺寸的图像，也就是人眼可分辨的细节部分像素宽度小于等于2个像素，这时需将图像尺度放大3倍或5倍[11]。其目的有两个：一是使后续边缘检测处理中获得的边缘宽度相对原图比例变小。边缘通常意义上的理解应该是没有宽度的曲线。在很大尺度的图像中一个像素宽度可忽略不计，视为无宽度；而小尺度图像一个像素宽度所占比例不容忽略，所以扩大小图像尺度有利于边缘检测的准确度。二是防止边缘检测后的膨胀、腐蚀算法对边缘表示的结果产生影响。以两条平行的边缘线为例，其间隔为一个像素，若对边缘进行形态变换。首先对边缘膨胀变换，一个像素的间隔将会被填补，两条平行线粘合为一体；再进行腐蚀变换，根据腐蚀规则粘合的两条平行线无法再被分离开。解决办法就是通过图像尺度拉伸，将原图长宽比例扩大3倍或5倍，边缘间的间隔也会大于或等于 3，这样向外一个像素的膨胀变换不会造成以上设想的那种粘连，从而消除了对分割造成的不利影响。

2）利用大津法对图像二值化

大津法由大津于 1979年提出，对图像M* N ，记pi为灰度i的像素点占图像比例数，t为前景与背景的分割阈值，前景点数占图像比例为q1( t)，平均灰度为u1( t)，方差为( t)；背景点数占图像比例为q2( t)，平均灰度为u2( t)，方差为( t)。图像的总平均灰度为

从最小灰度值到最大灰度值遍历t，当t使得(3)最小时即为分割的最佳阈值。这意味着当取阀值为t时，前景和背景的方差加权和最小，即前景和背景每部分的像素都比较平稳。

3）膨胀腐蚀等运算

将边缘线按图像形态学方法进行膨胀，从而使边缘区域向外延展以致间隔较小的隔间区域被连接起来，再采用开操作，可以对图像平滑边界、把比结构元小的斑点、突刺滤掉并能切断细长搭接而起到不必粘合的分离作用。

一般通过八邻域的膨胀扩张一个像素可以使最多2个像素间隔的断线连接起来；如果待分基元边缘断续间隔大于2个像素，且不同待分基元间的间隔大于边缘断续间隔，可以通过圆形膨胀多个像素的方法使断续边缘连通。完成膨胀后以同样形状模式和半径腐蚀被增粗的边缘使之细化，还原得到被修补断缝的边缘图。如图2的比较结果。

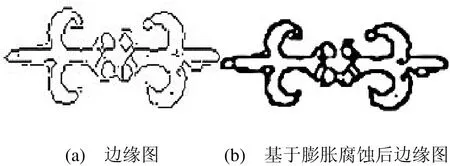
图2 膨胀腐蚀图

采用相同模板的膨胀腐蚀操作后，能够将大量断续的线段连接成整体，同时会造成原单像素的边缘线粗化，但不会造成片段信息的丢失。粗化后的图像尽管导致了边缘信息的不清晰，但它仍能准确描述图案形状。

4）块状区域的连通标记

通过八邻域连通标记，在一个图像中标记了每个连通区域的类别标签，标签从1开始，以此加1，直到连通区域的个数。对形成了类别标签的区域进行分类颜色填充（见图3）。

图3 连通标记图

3.1.2 图案基元切割

基于不同颜色的区域，进行图案基元切割，分离出独立的图案基元，由于分割图像基元的算法以连通区域为判断依据，算法易用，但同时会在图像基元集中产生有许多重复基元（旋转方向可能不同）和过小的无意义图像基元，需要进一步剔除。

如图4所示，经过图案分割后，形状相似的重复基元很多，在实际应用中，具有代表性的基元只需要保留一个。

图4 图案基元切割

3.1.3 图案基元特征提取

根据前面的分析，必须对分割的图案基元进行筛选，为此提取8个可以表征图案形状的几何参数作为其特征，用f1…f8表示。

其中，f1表示图案区域面积；f2表示图案边缘长度；f3表示图案区域的重心；f4表示图案边缘线的重心；f5表示边缘距离边缘重心最远距离；f6表示边缘距离边缘重心最近距离；f7表示边缘距离边缘重心最远点到区域重心的距离；f8表示边缘距离边缘重心最近点到区域重心的距离。

在图像识别和分类中，特征选择和提取是至关重要，而对于一个图案基元来说，其几何特征是非常重要的。论文从基元的区域、边缘入手，定位区域或边缘的重心、距离以及区域之间、边缘之间的重心、距离等几何参数，唯一确定并保留无重复基元。

3.1.4 基于图案相似度筛选纹样基因

根据提取的特征筛选出纹样基因，但不同特征在区别基元上具有不同的贡献，为此引入一个权重；又因为所有特征均为几何参数，其物理意义相同，但取值范围不同，故选用加权和的形式作为判断基元相似性的度量依据。

定义：将不同基元特征比的加权和作为基元相似度，其中权值可以利用用户的反馈调整，或根据投票策略进行判定。

设两个图像分别i,j，其8个参数分别为fik和fjk，k=1…8

相似度的计算公式为

由用户反馈的参数权重为wk，k=1…8，因此带权重的相似度公式为

理论上，当S趋于“1”为选择相似图案。实际上s并不一定趋于“1”，为此引入投票机制，计算中有5个以上接近于“1”就认为是相似图案。

根据特征比的加权和，将图像基元标识并排序，过滤相同标识的图案基元，得到唯一标识的纹样基因。

3.2 基于六边形堆砌的构型

分析民间图案的特点，发现基本元素具有重复并按对称构型进行排列组合的特征，其中六边形结构较多，为了实现相似民族图案构型设计，本文选用六边形结构，对每一结构内的纹样基因进行中心对称和轴对称折叠或旋转（见图5）。

首先将图案基因嵌入到一个正三角形中，然后将其上任意一点分别进行六次旋转变换，组成一个正六边形，如图6所示的六边形构型。最后将六边形构型堆砌平铺延展生成新疆民族织物图案，如下图6所示。

4 仿真与分析

4.1 纹样基因提取

纹样基因提取由连通标识分割、特征提取、计算两两图案基元特征比的加权和、过滤相似图案提取纹样基因组成。

1）选择一组新疆维吾尔族或哈萨克族的织物图案如图7所示。

2）利用连通标识算法如图8所示。

3）以图8(a)为测试用例，分割提取图案基元231个，部分图案基元显示如图9所示。

4）以图8(a)为测试用例，提取所有图案基元的8个特征参数如表1所示。

图5 六边形构型堆砌纹样基因

图6 堆砌六边形构型的平铺延展

图7 一类新疆民族织物图案

图8 织物图案分割结果

图9 图案基元

表1 图案基元的特征参数（以231个图案基元中的前10个基元为例）

5）以图8(a)为测试用例，针对提取的所有图案基元231个，计算任意两个基元之间相似度，过滤出不同相似度的纹样基因 49个，显示其中部分如图10所示。

图10 从图8(a)中提取纹样基因（显示49个基因中10个）

4.2 基于纹样基因的新疆民族织物图案生成

通过分析民间图案的特点，发现基本元素具有重复排列组合的特征，多以纹样基因和六边形结构进行堆砌形成。为此对每一结构内部的纹样基因进行中心对称和轴对称折叠或旋转。如图11所示，生成图案是由纹样基因通过镜像、等分角度旋转，构成的具有中心旋转及轴对称性质六边形图案。

图11 基于图10的纹样基因生成风格图案

4.3 风格测评基于纹样基因生成的图案

随机选择30名少数民族作为测试者对15幅图案（序号1～10为图11生成图案，序号11～15幅为图7中的原始图案）进行风格测试，测评选项有：风格相似，不相似，中立3种选择，结果如表2所示。

表2 生成图案的风格相似度测评表

分析：对于前 10幅生成图案的风格相似度评价均值为65%，后5幅真正民族织物图案的风格相似度评价为71.33%，说明少数民族对本民族的织物图案有较一致的认可程度，而生成图案中运用了纹样基因，传承了民族风格和特色，因此也得到了较高的风格认同，可以“以假乱真”应用于民族图案设计中。

5 结 论

针对织物CAD中对图案分割的要求，本文提出纹样基因的概念，并设计了基于特征筛选、过滤图案基元提取纹样基因生成民族织物图案的方法。该算法在保证原有民族织物图案风格基本不变的情况下, 产生新的纹样图案。从给出的大量实例中，可以看出方法的简单实用性，并可以在生成图案中方便地找到纹样基因，使得民族艺术图案的风格保留传承，为新疆纺织原料的花型、设计提供新的途径，为不同民族织物图案的建模奠定基础。

[1]潘云鹤. 综合推理的研究[J]. 模式识别与人工智能,1996, 9(3): 201-208.

[2]蔡沐芳, 梁惠娥. 国内外数码印花图案设计现状分析[J]. 丝绸, 2006, (10): 34-36.

[3]Prusinkiewicz P, Hammel M, Mjolsness E. Animation of plant development [J]. Computer Graphics, 1993,7(3): 351-360.

[4]Barnsley M F, Demoko S. Iterated function systems and the global construction of fractals [J]. Proc. R. Soc.Lond. A 8 June 1985, 399: 243-275.

[5]Kawaguchi Y. A morphological study of the form of nature [J]. Computer Graphics, 1982, 16(3): 223-232.

[6]Stephen W. Statistical mechanics of cellular automata [J].Review of Modern Physics, 1983, 55(3): 601- 644.

[7]Pentland A. Fractal-based description of natural scenes [J].IEEE Transactions on Pattern Analysis and Machine Intelligence, PAMI-6, 1984, (6): 661-674.

[8]Lindenmayer A. Mathematical models for cellular interaction in development, Parts 1 and part2 [J].Journal of Theoretical Biology, 1968, 18: 280-315.

[9]张显权, 于金辉, 蒋凌琳, 等. 计算机辅助生成剪纸形象[J]. 计算机辅助设计与图形学学报, 2005, 17(6):1378-1382.

[10]Liu Yanxi, James H, Xu Yingqing, et al, Digital paper cutting [C]//ACM SIGGRAPH 2005, 2005: 99-103.

[11]赵海英, 彭 宏, 杨一帆. 基于边缘形态变换的彩色织物图像分割算法[J]. 中国体视学与图像分析,2011, 16(1): 5-10.