基于三次PH曲线误差可控代数曲线等距线逼近算法

寿华好， 江 瑜， 缪永伟

（1. 浙江工业大学理学院，浙江 杭州 310023；2.浙江工业大学计算机科学与技术学院，浙江 杭州 310023）

等距曲线在工业设计领域有着广泛的应用，例如，数控加工中车床的刀具中心轨迹的计算，机器人行走路线规划，以及汽车外形的设计, 碰撞检测等与CAD/CAM相关的领域。但在通常情况下，平面参数曲线或代数曲线的等距线并不具有多项式或有理多项式表达形式，这与CAD/CAM系统不兼容。为此，许多学者进行了大量深入的研究，如Lee等[1]首先在1996年提出了使用单位圆弧段逼近的N次Bézier曲线等距线生成算法。该算法首先使用Bézier曲线逼近单位圆弧段，然后生成该单位圆弧段与原始曲线的卷积曲线，最后利用卷积曲线逼近Bézier曲线等距线。Lee算法的优点是具有明确的误差范围，但卷积曲线是3N-2阶的有理Bézier曲线，当待求等距线的Bézier曲线次数N 比较大时，计算量非常大。由于Lee算法使用有理Bézier曲线逼近等距线，与其它求取等距线算法相比没有明显优势，所以基于单位圆弧段算法没有引起研究者注意。直到2004年Ahn等[2]进一步将卷积曲线表示为与原曲线等次数的Bézier曲线，解决了Lee算法在Bézier曲线的次数N较大时的计算量偏大问题。但Ahn算法只使用二次Bézier曲线逼近单位圆弧段，精度较低。2004年郑志浩等[3]提出了用三次PH曲线构造平面Bézier曲线的等距线算法。该算法是根据Bézier曲线的始末端点及其切向量，加入节点，使其满足PH曲线的条件，以此构造出来的PH曲线来逼近原Bézier曲线，并进而生成等距线。该算法通过增加节点数可控制逼近误差在所需的范围内，本文引用文献[3]中构造PH曲线的方法，用PH曲线来逼近平面代数曲线，并生成PH曲线的等距线，作为平面代数曲线等距线的近似表示。

基于逼近算法计算比较简单的考虑，这里给出的代数曲线的PH曲线逼近有自身的特点: 曲线分段时同时考虑了拐点和极值点，使得逼近曲线保持原始曲线的凹凸性的同时保持单调性和G1连续性。递归调用逼近算法，可以将误差控制在指定的范围之内。而用PH曲线的精确等距线逼近原代数曲线的等距线，无需采用细分策略，通过误差分析可知采用本算法所获得逼近精度大大得到了提高。

1 三次PH曲线的定义及性质

本文的研究建立在三次PH曲线的基础上，所以需要先考查三次PH曲线的几何性质。

定义 1[4]PH曲线((),())x ty t 为满足如下条件的平面参数曲线

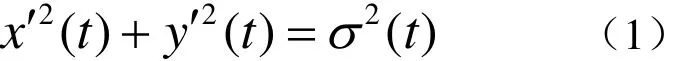
其中，σ(t)是一个多项式。

引理 1[3]一个三次Bézier曲线是PH曲线的充要条件是

其中，p0，p1，p2和p3分别是三次PH曲线的控制顶点，L1,L2,L3分别为三次PH曲线的边长（如图1所示）。

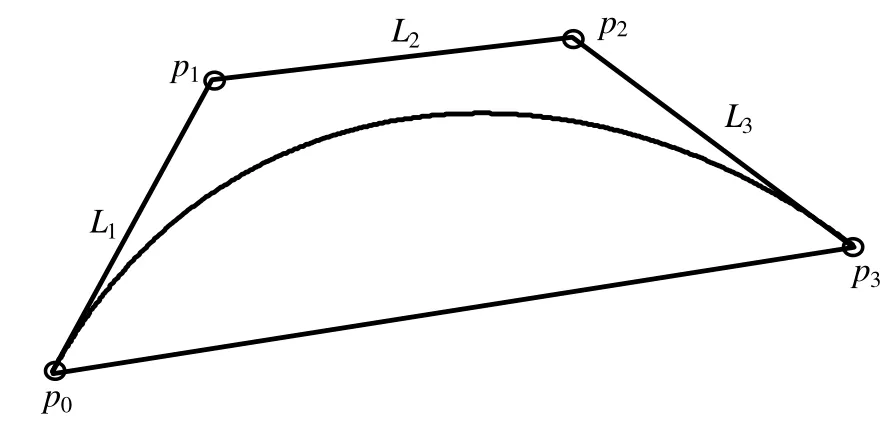
图1 三次PH曲线

定义 2 PH曲线等距线

N次PH曲线p( t)的等距线 pr( t)可以被定义为

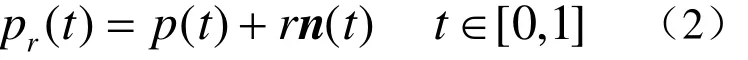
其中，r为等距距离，n(t)是p( t)的单位法向量，它可以通过p( t)的单位切向量旋转π/2得到，具体的计算公式为

2 用三次PH曲线逼近平面代数曲线

2.1 对代数曲线进行分段并计算每段子曲线两端点处的切线

首先将代数曲线进行分段[5]使得代数曲线在每个分段区间上具有固定的凹凸性和单调性。然后计算每段代数曲线两端点处的切线[6]。

2.2 控制多边形的确定

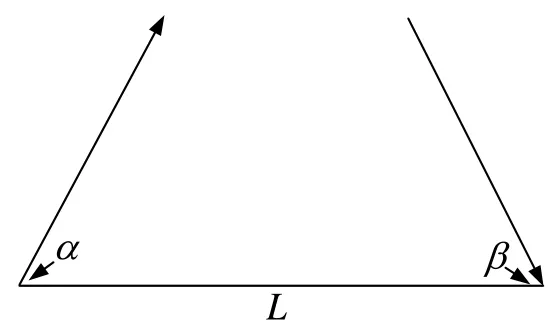
图2 给定曲线两端点的位置及其曲线在端点处的切线方向

图3 构造出的PH曲线的控制多边形

这是一个关于L2的一元二次方程，由此可以解得L2，再由

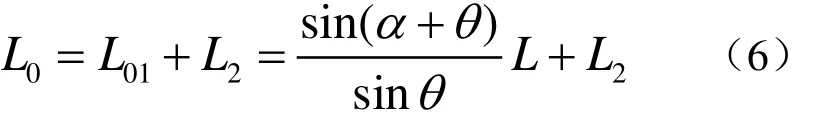
可以得到L0，由此三次PH曲线的控制多边形就可以确定了。

2.3 等距线生成

3 分段逼近误差

3.1 逼近误差

设A为代数曲线段，p( t)为逼近曲线段，在几何学中，曲线A和它的逼近曲线之间的误差经常使用Hausdorff距离来表示，但是这种距离便于理论分析而不便于计算。下面给出一种易于计算的误差概念。

3.2 算法的基本步骤

1）先对原始代数曲线进行分段（涉及拐点和极值点的计算，计算代数曲线拐点和极值点的算法见参考文献[7]）；

2）计算曲线段A两端点处的切线及其与弦长的夹角；

3）根据式(4）～(6)计算PH曲线的控制多边形；

4）若逼近误差 e( A, p( u ) )＜δ，则计算过程终止，否则，采用逐步二分分段区间的方法，递归调用上述分段逼近算法，直至满足给定的误差要求。

5）计算逼近PH曲线的等距线，以它来逼近原代数曲线的等距线。

4 实 例

曲线C的整体逼近效果如图4所示。图中虚线表示原曲线，实线是用分段PH曲线逼近得到的结果，分段PH曲线的逼近效果非常好。

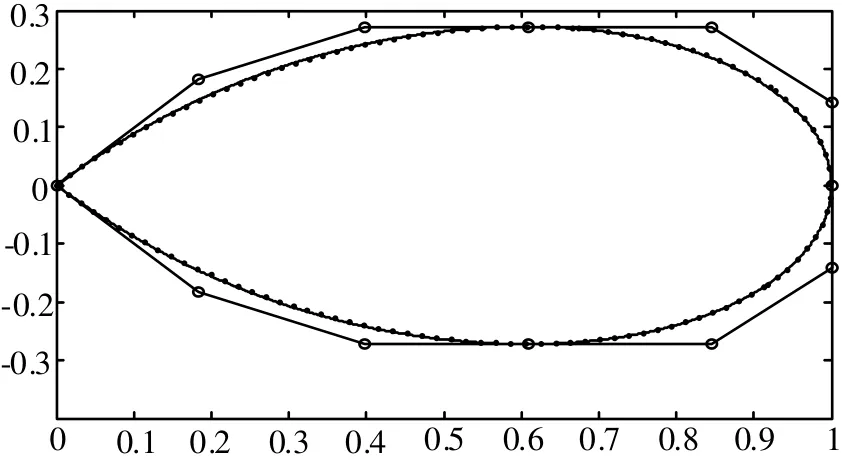
图4 曲线C的右四分之一及它的PH逼近曲线

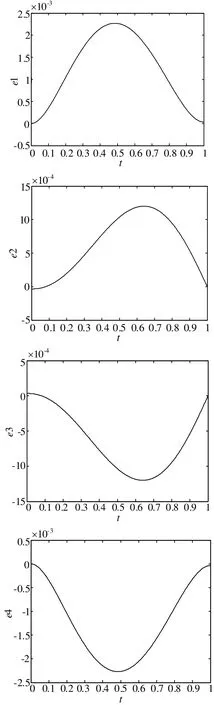
图5 曲线C的右四分之一的分段误差函数图形（依次为左上段、右上段、右下段、左下段）

根据定义2计算出4段PH曲线的等距线如图6所示。由于等距线不过是生成曲线在法线方向上平移距离r后得到，从而只要逼近PH曲线和原代数曲线的误差小于δ，那么逼近PH曲线的等距线（即逼近等距线）与原代数曲线的等距线（即精确等距线）的误差一定也小于δ。

对于上图内外两条等距线，外面一条没有封闭上的情况，可以原点为圆心，等距距离r为半径做一段圆弧；而对于里面一条出现交叉的现象，可求出交点，然后将多余部分裁减掉。图7是处理后的结果。

图7 处理后的图形

5 结 论

代数曲线的分段三次PH逼近算法简单有效，逼近曲线保持了原曲线的凹凸性，单调性，G1连续性等重要几何性质，通过算法的递归调用，可以将逼近误差控制在给定的范围之内。另外，通过增加曲线的分段可控制逼近误差与等距误差，从而生成由同样低次数、结构统一、便于数据存储的等距线。

[1]Lee I K, Kim M S, Elber G. Planar curve offset based on circle approximation [J]. Computer-Aided Design,1996, 28(8): 617-630.

[2]Ahn Y J, Kim Y S, Shin Y. Approximation of circular arcs and offset curves by Bézier curves of high degree [J].Journal of Computational and Applied Mathematics,2004, 167(2): 405-416.

[3]郑志浩, 汪国昭. 用三次PH曲线构造平面Bézier曲线的等距线算法[J]. 计算机辅助设计与图形学学报，2004, 16(3): 324-330.

[4]雍俊海, 郑 文. 一类五次PH曲线Hermite插值的几何方法[J]. 计算机辅助设计与图形学学报, 2005,17(5): 990-995.

[5]胡 斌, 梁锡坤. 代数曲线的分段有理二次B样条插值[J]. 计算机工程与应用, 2007, 43(24): 55-58.

[6]黄群宾, 邓 鹏. 一种求代数曲线的切线与渐近线的初等方法[J]. 四川师范学院学报, 2001, 22(4):389-391.

[7]Shou Huahao, Shen Jie, Yoon D. Numerical computation of singular and inflection points on planar algebraic curves[C]//Hamid R A (Ed.),Proceedings of 2007 International Conference on Computer Graphics & Virtual Reality, CSREA Press,USA, 2007: 133-138.