合龙段底板分层破坏抗裂设计方法研究

2012-07-07林海峰张冬冬赵启林

中国工程科学 2012年5期

林海峰，张冬冬，赵启林

(1.江苏省长江公路大桥建设指挥部，江苏泰州 225321;2.解放军理工大学工程兵工程学院，南京 210007)

1 前言

合龙段及其附近底板的分层破坏是悬浇预应力混凝土箱梁桥在施工期内最为普遍的一种破坏形式。传统研究普遍认为因为底板连续束的径向分力导致管道之间混凝土出现拉应力，尤其当管道之间会面为薄弱面，竖向拉应力较大，拉应力超过混凝土抗拉强度时，在该剖面出现沿横向的上下分层破坏现象。为此，许多桥梁对径向力导致的竖向拉应力进行了简化计算或者三维有限元计算分析，但是计算得到的竖向拉应力往往小于混凝土抗拉强度设计值，这样即使不设置勾筋等普通钢筋，底板也不会出现横向裂缝，更不会出现分层破坏现象。

事实上，许多桥梁还是在跨中连续索张拉过程中出现了严重的分层现象，究其原因是在设计中没有考虑到底板的特殊受力状态，没有选择更为合适的混凝土强度破坏准则。事实上，在底板索张拉过程中，底板的混凝土不仅受到竖向拉应力作用，还受到强大纵向压应力作用，即处于双轴拉/压的应力状态，因此所采用的最大拉应力准则是不合适的，而应该采用双向应力状态下的混凝土强度破坏准则。为此，文章选择多座发生底板分层破坏以及没有发生分层破坏的典型桥梁作为研究对象，采用有限元法计算其底板预应力束管道之间的应力状态，随后将底板计算应力分别带入不同的判别准则中以预测底板出现开裂的可能性，并在桥梁施工过程中对一些桥梁底板应力状态进行了跟踪监测，从而判断哪种准则更适合解决底板的分层破坏问题，进而为底板的抗裂设计提供参考。

2 混凝土强度破坏准则

变截面混凝土箱梁一般都采用全预应力结构，在1985年与2004年公布的《公路钢筋混凝土及预应力混凝土桥涵设计规范》中均对混凝土开裂控制提出了相应的设计计算要求，但是该类型桥梁出现开裂的概率与严重程度明显高于其他类型的混凝土桥梁，究其原因，除了部分施工控制误差等原因外，与规范所提出的混凝土抗裂设计计算理论不能完全适用于挂篮施工的变截面预应力混凝土箱梁桥也有密切关系。具体地说，以往的桥涵设计规范更多的是将桥梁结构按受弯构件、受压构件、受拉构件、受扭构件等一维或二维的构件进行应力状态计算，而构件混凝土的抗裂验算都是基于第一主拉应力准则，即认为混凝土开裂都是混凝土拉应力值超过抗拉强度导致的，混凝土只会发生拉断一种破坏形态。事实上，变截面预应力混凝土箱梁桥有明显的三维空间效应，许多部位的混凝土处于多轴应力状态下，而多轴应力状态下的混凝土不仅拉断破坏形式，而且有柱状压坏、片状劈裂、斜剪破坏、挤压流动等其他破坏形式［1］。因此，选择合适的混凝土破坏准则对预测混凝土材料承载力有重要影响。

2.1 最大拉应力准则［2］

最大拉应力准则(maximum tensile stress criterion)是1876年由Rankin提出的，该准则假定:当最大拉应力超过材料的极限值时，认为发生破坏。该准则提出后，大量学者对其适用性进行了研究，已经指出该准则主要适用于承受拉伸和较小压应力下材料破坏的描述［3］，而不符合混凝土在多轴压力作用下的情况。只要当此点上的最大主应力达到简单拉伸实验得出的材料抗拉强度ft时，就认为混凝土发生脆断，无论通过材料内一点在其他平面上产生的正应力或剪应力如何。根据这一准则确定的破坏面方程为

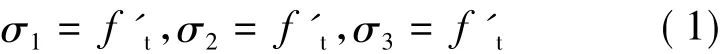
式(1)中，σi(i=1，2，3) 为主应力，f't=nft(其中f't为单轴抗拉强度，n为换算系数，ft为由简单拉伸实验得出的材料抗拉强度)。式(1)也可采用( I1，J2，θ)或 (ρ，ξ，θ)的形式，其中 I1为主应力不变量，J2为主应力偏量不变量，ξ、ρ、θ分别为采用柱坐标系时的静水压力、偏平面应力、相似角。于是得到了如图1所示的垂直于3个主应力轴的3个平面，该平面称为“裂断面”或“拉伸破坏面”。

图1 最大拉应力准则(拉断)Fig.1 Maximum tensile stress criterion(snap)

2.2 双向应力准则

有些钢筋混凝土结构的受力状态可以合理地简化为平面应力状态，它与单轴应力下的情况相差较大，主要分为双轴受压、双轴拉—压、双轴受拉3种情况。大跨度变截面预应力混凝土箱梁桥一般在结构内部施加了较大的纵向和竖向压应力，而由于跨中连续索的径向力、锚固力等作用产生的局部横向与竖向拉应力一般较小，因此该类型桥梁结构并不适合采用最大拉应力强度准则，而适合用双轴应力强度准则来进行抗裂的控制设计。目前，较常用的双轴应力强度准则主要有 Kupfer＆Gerstle准则与《混凝土结构设计规范》推荐的简化判别准则。

2.2.1 Kupfer ＆ Gerstle 准则［4］

目前用于描述双轴应力下强度的数学模型有许多，其中以Kupfer＆Gerstle准则最为典型，公式形式简单，采用的参数少且精确性较好，至今仍然被广泛采用，其表达式为双轴受压

式(2) ～(4)中，系数a= σ1/σ2;f'c和f't分别为混凝土单轴应力情况下的圆柱体抗压强度和抗拉强度;σ1c和σ2c分别为双轴应力下σ1和σ2方向混凝土的抗拉(压)强度。由式(2)～式(4)可见，当混凝土处于双向压应力作用下时，混凝土抗压强度高于单轴应力下的混凝土抗压强度;当混凝土处于拉—压双向应力作用下时，混凝土抗压与抗拉强度均将下降，其中竖向抗拉能力最低可能只有单向抗拉强度的20%左右;当混凝土处于双向拉应力作用下，混凝土抗拉强度与单轴应力下混凝土抗压强度相当(见图2)。

图2 双轴应力下混凝土强度包络图Fig.2 Envelopes of concrete strength under biaxial stress

2.2.2 《混凝土结构设计规范》推荐的简化判别准则［4］

为了使混凝土结构抗裂设计更符合材料的基本特性，我国《混凝土结构设计规范》(GB 50010—2002)中不仅新增了混凝土的多轴强度和本构关系，而且将混凝土多轴强度验算进行了简化，便于设计人员进行多轴应力状态下的混凝土抗裂设计。在规范中规定:多轴强度不是按照第一主应力进行验算，而是进行三个或两个主应力的联合验算，即 σi≤ fi(i=1，2，3) ，其中，σi是第 i方向主应力，fi是第i方向的许用应力，只有3个方向的主应力都满足上式，结构才是安全的，对于双轴应力下的fi(i=1，2，3)，结合图3按照表1进行计算。

表1 二轴强度计算式Table 1 Biaxial strength formula

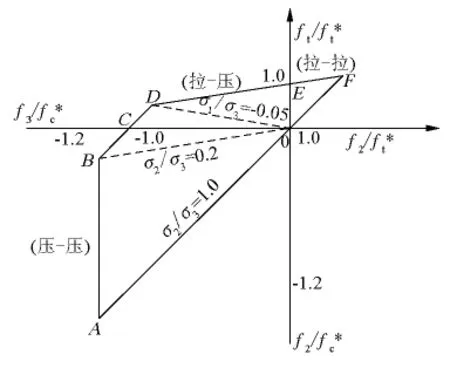
图3 GB 50010—2002推荐采用的双向应力下混凝土强度包络图Fig.3 Envelopes of concrete strength under biaxial stress that the GB 50010—2002 recommends

2.3 现行《桥规》采用准则及其不足［5］

现行《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 62—2004)中的箱梁抗裂验算是基于最大拉应力准则的，分为正截面抗裂验算和斜截面抗裂验算。

在进行正截面抗裂设计时，应对正截面混凝土的拉应力进行验算，要求拉应力符合以下要求:

1)对于预制的全预应力混凝土构件，在作用短期效应组合下，σst≤0.85σpc≤0;

2)对于分段浇筑或砂浆接缝的纵向分块构件，在作用短期效应组合下，σst－0.80σpc≤0;

3)对于A类预应力混凝土构件，在作用短期效应组合下，σst－ σpc≤0.7ftk;

4)对于A类预应力混凝土构件，在作用长期效应组合下，σlt－σpc≤0。

其中，σlt，σst分别为作用短期效应组合、作用长期效应组合下构件抗裂验算边缘混凝土的法向拉应力，按式(5)计算

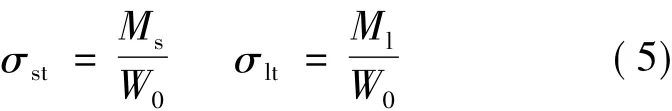
式(5)中，Ms，Ml分别为作用短期、长期效应组合计算的弯矩值。

在进行斜截面抗裂设计时，要求对构件斜截面混凝土的主拉应力σtp进行验算，即符合下列要求:

1)对于预制或现场浇筑构件，在作用短期效应组合下，σtp≤0.6ftk或 σtp≤0.4ftk;

2)对于预制或现场浇筑的A类和B类预应力混凝土构件，在作用短期效应组合下，σtp≤0.7ftk或 σtp≤0.5ftk。其中，ftk为混凝土抗拉强度标准值，而ftk前的系数为表达材料离散性的各种安全保证系数，σtp为由作用短期效应组合和预应力共同产生的混凝土主拉应力，按式(6)计算

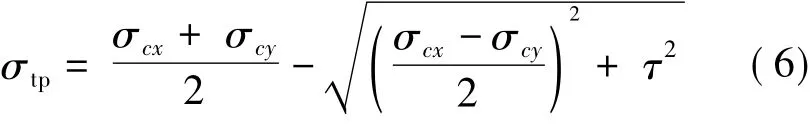
式(6)中，σcx为在计算主动点的混凝土法向应力;σcy为计算主动点竖向压应力;τ为计算主应力点的混凝土剪应力。

目前的桥梁设计规范在进行受弯构件的抗裂验算时，按照第一主拉应力进行混凝土抗裂验算本身在理论上就是不完善的。因为根据大量实验已经证明［1］:混凝土在双向受压时的极限强度比单向受压强度大，应力比为0.5时增长最大，约为22%;在压—拉情况下，混凝土抗压强度与抗拉强度都明显下降;双向受拉时的强度与单向受拉强度基本相同;所有单向、双向应力状态下实验破坏形式的破坏面均与最大拉应变方向正交，破坏时拉应变大小是固定的，但是随受压程度增加而增加，表明混凝土可承受的非直接受拉应变能力明显大于直接受力受拉应变能力。由此可见，双向应力状态下混凝土抗拉强度是受另外一个方向压应力影响的，但是《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 62—2004)中是按照第一主应力小于混凝土抗拉强度来验算，如果假定τ=0，X方向应力σcx为拉应力，Y方向应力σcy为压应力，则式(6)可以简化成σtp=σcx，则抗裂控制方程为σcx≤aftk。因而，在双向应力状态下，抗裂验算只与X方向的拉应力值有关，而Y方向的压应力值σcy无关，这明显与实验结论是不一致的。

由前述描述与分析可见，现有桥梁设计规范抗裂设计计算理论是滞后于混凝土基本理论发展的，因此，该类型桥梁结构并不适合采用最大拉应力强度准则，而更适合选用更符合混凝土基本受力特点的双轴应力强度准则来进行抗裂的控制设计。

3 案例分析

为了对前述不同准则在抗裂验算时的有效性进行对比，本节将选取8座典型桥梁实例(其中4座为破坏案例，另外4座为没有破坏案例)进行ANSYS有限元建模与计算，分别得到其合龙段底板预应力管道间的竖向拉应力与纵向压应力，以便进行进一步的安全性预测。

3.1 模型参数

选取的所有典型桥梁均采用变高度单箱单室直腹板截面，主桥箱梁采用纵、横、竖三向预应力体系，混凝土标号为C50，其他基本参数见表2。

表2 典型桥梁的基本参数Table 2 Basic parameters of the typical bridges

3.2 ANSYS模型的建立

桥梁三维建模采用大型通用有限元程序ANSYS10.0，预应力钢束用 LINK8杆单元，混凝土用Solid 65六面体单元来模拟，考虑到结构的对称性，以及施工时荷载的正对称性，为了控制计算规模，选取箱梁中跨的1/4结构进行计算。边界条件如下:在切开面均采用对称约束，约束箱梁支座位置节点的全部自由度来模拟梁墩临时固结的情况。预应力筋采用实体力筋法，由杆单元的初应变来模拟，顶板、腹板钢束的节点与离得最近的混凝土单元节点耦合;底板预应力钢束节点与混凝土单元共节点。非预应力钢筋对混凝土结构应力的影响，通过Solid65实体单元与配筋率相关的实常数来考虑。图4是其中建立的破坏案例4的ANSYS整体模型与合龙段局部模型(由于篇幅限制，其他桥梁的有限元模型未列出)。

图4 破坏案例4的ANSYS整体模型与合龙段局部模型Fig.4 The overall ANSYS model and the closure segment’s partial ANSYS model of failure case 4

3.3 合龙段底板管道间应力计算结果

考虑到合龙段底板的预应力孔道处横截面是整个底板最薄弱的环节，因此重点考察合龙段底板在预应力孔道中心切面上的应力状态，如图5所示。空间应力结果分析中，X向指的是横向，Y向指的是竖向，Z向指的是纵向，应力正值为拉，负值为压。所有典型桥梁的合龙段预应力管道之间的竖向应力与纵向压应力计算结果见表3。

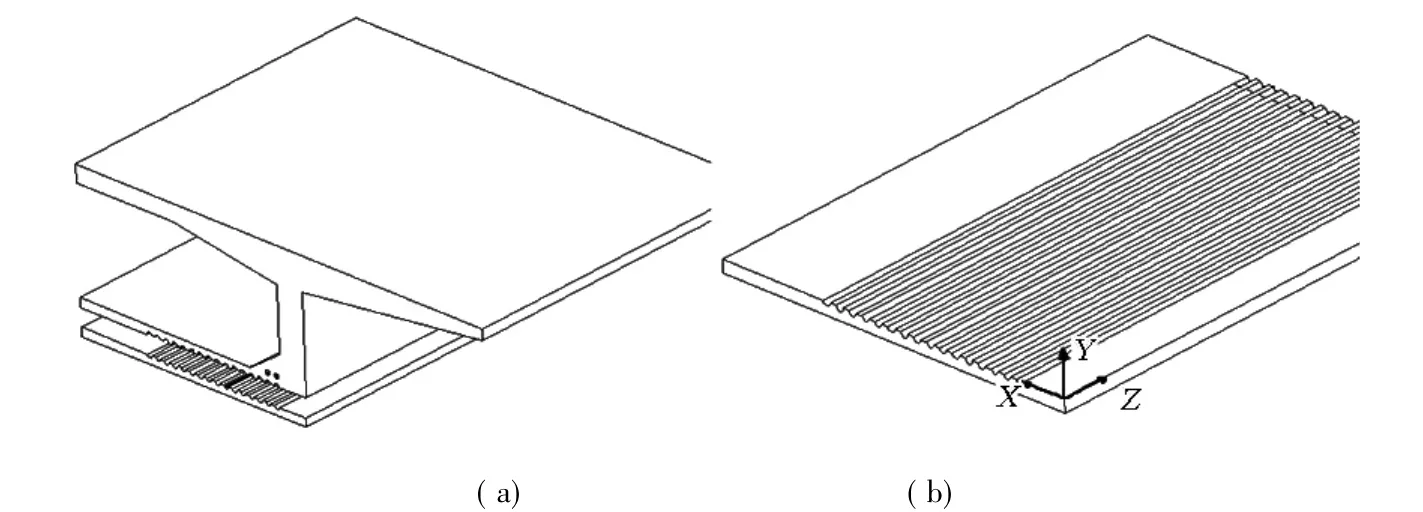
图5 底板预应力孔道中心处剖面示意图Fig.5 Diagram of cross section of the central of pre-stressed tendon at bottom slab

表3 典型桥梁底板预应力管道之间的应力状态Table 3 Stress state between pre-stressed tendons of the typical bridges

3.4 底板分层破坏安全性预测

为了验证在不同准则下的底板抗裂是否安全，本节将前节得到的纵向压应力均值、管道之间最大拉应力值计算结果以及C50抗拉强度设计值、标准值(见表3)分别代入前述《公路钢筋混凝土及预应力混凝土桥涵设计规范》(JTG 62—2004)、Kupfer＆Gerstle准则以及《混凝土结构设计规范》(GB 50010—2002)推荐的简化判别准则中的相应计算公式中，分别利用不同准则对底板的安全性进行预测，并与典型桥梁实测破坏结果做了对比。其中，在《桥规》的计算中，C50混凝土抗压、抗拉强度标准值分别为32.4 MPa与2.65 MPa，抗压与抗拉强度设计值分别为22.4 MPa与1.83 MPa。不同准则下的典型桥梁应力状态计算结果对比见表4。

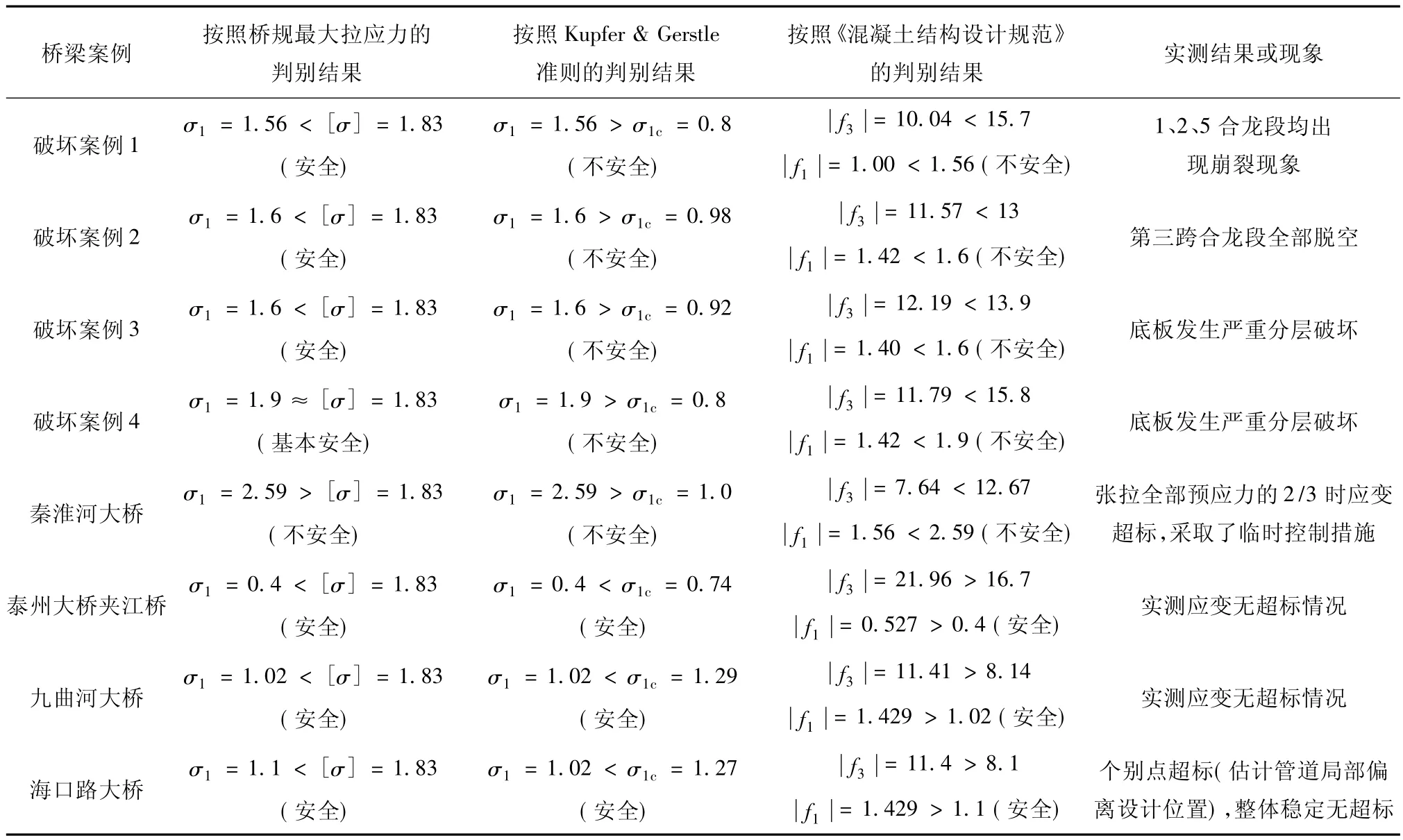
表4 利用不同准则对比典型桥梁应力状态Table 4 Stress state of the typical bridges under different Criteriaes

由表4可见，按照最大拉应力准则进行底板分层抗裂安全性预测时，8座桥梁只有一座桥的预测结果与桥梁的设计状态相一致;而按照拉—压双向应力破坏准则进行预测，8座桥梁有7座桥梁预测结果与桥梁实测状态是一致的，因此大跨度变截面预应力混凝土箱梁桥的底板分层破坏更应该采用双向应力强度破坏准则来进行判别。建议按照我国《混凝土结构设计规范》(GB50010—2002)提出的双轴强度准则进行混凝土抗裂设计。