基于ANSYS的悬索桥分析方法研究
2012-07-07谢雪峰罗喜恒
谢雪峰,罗喜恒
(1.同济大学桥梁工程系,上海 200092;2.同济大学建筑设计研究院(集团)有限公司,上海 200092)
1 前言
悬索桥分析程序可以分为专用程序和通用程序。专用程序如平面缆索悬索桥数值分析程序SBP、CAP(construction analysis program for suspension bridge)[1]和悬索桥分析系列程序[2]以及悬索桥主缆设计与施工计算专用软件SGK2000、桥梁结构空间几何非线性静动力分析软件BCAS2000[3]等。通用程序主要有桥梁博士、Midas/Civil、ANSYS、SAP2000等。专用程序和通用程序在悬索桥分析方面各有优缺点,如专用程序具有能考虑悬索桥的特殊构造、加载方便等优点,计算速度较快,计算精度较高,但前后处理一般配合不好,有些程序还有些缺陷;而通用程序前后处理方便,但一般没有专门的鞍座单元、顶推单元,并需要人为给出主缆和吊索的无应力长度。
笔者在ANSYS平台基础上进行二次开发,结合悬索桥的特点构造了鞍座单元和模拟鞍座顶推的算法,编写了主缆和吊索无应力长度的迭代求解APDL程序,使得ANSYS在悬索桥分析方面具有了专用程序的结构模拟精度和计算精度,并且具有良好的前后处理功能。
2 分析方法
2.1 鞍座的模拟
鞍座是使主缆平顺转向的构件,计算时一般认为主缆应总是与鞍座相切的,然而在施工阶段和活载作用过程中,塔顶会有比较大的位移,主缆与鞍座的切点位置也有比较大的变动,因此,正确模拟鞍座及切点的变化,是很有必要的。
以塔顶鞍座为例,如图1所示,鞍座单元的构造如下:A为鞍座标识线(成桥时与主塔中心线重合)上的主缆点,为主缆与鞍座的固定点;B为鞍座标识点,成桥时与塔顶中心点重合;C、D为主缆与鞍座的切点;E、F为主缆上的节点。单元AB、AC、AD为刚臂单元,采用mpc184单元。CE、DF为索单元,采用link10单元。BHG为顶推刚臂单元。
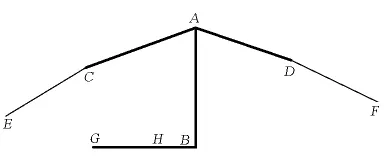
图1 鞍座单元构造形式Fig.1 Saddle element form
在鞍座顶推或活载作用下,鞍座两侧圆弧段的圆心相对于AB是不变的,也就是说,可以根据AB的转角和索单元CE、DF在C、D点的切线角更新切点C、D的位置,直至前后两次索单元CE、DF在C、D点的切线角相差小于给定的限值,则认为相切。一般只需更新两到三次就能达到较高精度。
以下以D点为例给出其原理。假设圆弧AD的圆心为O(Ox,Oy),半径为R,设AB长为l,且逆时针摆动α角,主缆在D点的切线与水平向夹角此时为β,则更新D(xd,yd)点位置如下:
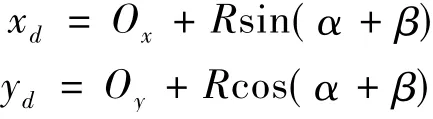
散索鞍的构造同上,只是摆动式散索鞍没有顶推刚臂BHG。
2.2 顶推的实现
在施工过程分析时,需要模拟顶推鞍座这一悬索桥特有的工况。如图2和图3所示,顶推过程的模拟采用以下单元构造形式:BGI为mpc184滑块单元,B为滑块;HGI为mpc184滑块单元,H为滑块;BH、GH、B’I、B’G 为 mpc184 刚臂单元,B’J为塔顶梁单元。赋予单元GH一个合适的线膨胀系数,通过改变GH的温度即可实现鞍座顶推的模拟。如单元GH的长为2 m,线膨胀系数设为1,以当前工况为基准,降温该单元0.5℃则顶推1 m。在施工阶段分析时可以通过杀死GH单元来实现鞍座能随施工过程自由滑动的情况,从而获得滑动量和塔顶水平力随施工过程的变化曲线,进而合理设计顶推次数和顶推量。
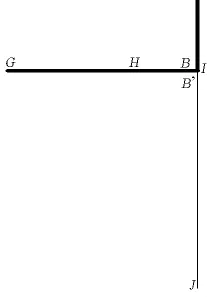
图2 顶推单元构造形式Fig.2 Incremental launching element form schematic diagram
2.3 主缆和吊索无应力长度的确定
主缆和吊索无应力长度求解,一般采用文献[1]中公式(2.1)和(2.2)进行迭代求解。然而,在利用ANSYS进行悬索桥分析时候,如果可以用AP-DL(ANSYS parametric design language)语言进行迭代求解出无应力长度,则模型一气呵成,修改起来也很方便,提高了工作效率。以下是迭代过程的基本原理和流程图。
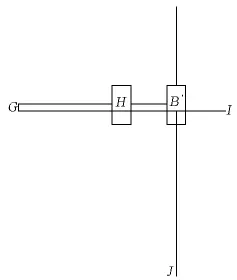
图3 顶推单元示意图Fig.3 Incremental launching element
2.3.1 基本原理[4]
1)原理1:非线性方程求解的Newton-Raphson方法。采用Newton-Raphson方法,每步迭代都要计算导数值。在该问题中,是无法计算出导数值的,因此采用两点割线法,以差商代替导数,见图4。迭代公式如下:
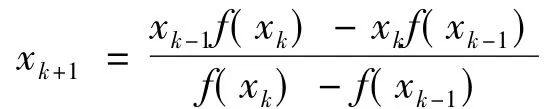

图4 牛顿-辛普森法Fig.4 Newton-Raphson method
2)原理2:非线性方程组求解的迭代法。F:D⊂Rn→ Rn是 n元实向量函数,把非线性方程组F(x)=0改写成不动点迭代x=G(x),则有如下定理:
设G:D⊂Rn→Rn在区域D0⊆D上满足G把D0映入它自身,即G(D0)⊆D0;G在D0上是压缩映射,压缩因子为L<1,即对任意x,y∈D0有
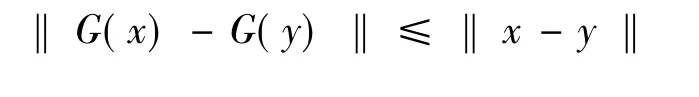
则下列结论成立:a.G在D0上存在唯一的不动点x*;b.对于任意的x(0)∈D0,不动点迭代x(k+1)=G(x(k))产生的迭代序列 { x(k)}⊂D0且收敛于唯一的不动点x*。
2.3.2 基本原理的应用
2.3.2.1 原理1 的应用
以中间跨为例,定义函数
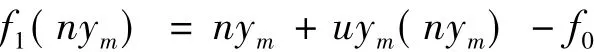
即跨中节点在恒载作用下竖向位置与设计竖向位置的差值为跨中节点竖向坐标的函数。式中,nym为跨中节点的竖向坐标;uym为跨中节点在恒载作用下的竖向位移;f0为跨中节点的设计竖向位置。
以边跨为例,定义函数
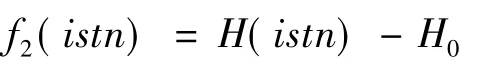
即边跨主缆在恒载作用下水平力与中间跨的成桥状态水平力的差值为边跨主缆单元初应变的函数。锚跨和边跨相同。式中,H为边跨主缆在自重和索夹重等作用下的水平力;H0为中间跨的成桥状态水平力;istn为边跨主缆单元的初应变。
2.3.2.2 原理2 的应用
一般情况下,按照设计的成桥位置建立缆索系统的初始模型。在恒载的作用下,上下吊点会发生水平位移和竖向位移。为了使成桥时各吊点位于设计位置,在迭代过程当中,需要修改上吊点的水平坐标和下吊点的竖向坐标。
以上吊点水平坐标为例,设其个数为n组成向量 x(x1,x2,…,xm,…,xn) 。向量 nx0表示吊杆上节点的成桥状态在恒载力作用下的水平位置,即目标位置。构造向量nx=nx0-ux,ux表示上吊点的水平位移。nx满足原理2的条件,在迭代过程当中,逐次更新吊杆上节点的水平坐标为nx,直至收敛。
2.3.3 迭代流程
以控制点为依据建立成桥状态初始模型,先假定各个切点的位置,中间跨以两切点和跨中点为依据,按照抛物线来确定其他节点坐标;锚跨和边跨以两切点间连直线段为依据,确定其他节点坐标。初始的缆索单元初应变设为1.0E-8。以中间跨迭代求无应力长度为例,迭代流程如图5所示,其中Y0、Y1为跨中节点竖向坐标,函数 f即2.3.2节中的函数f1。根据2.3.2可知,缆索系统的未知量:缆索单元的无应力长度,其个数与迭代方程个数相等[1,3],可迭代求解出缆索系统的线形和无应力长度。

图5 中间跨迭代流程Fig.5 Main span iterative process
2.4 无应力长度保持不变的方法
按照上述方法迭代出缆索系统的无应力长度之后,在鞍座顶推或活载作用下,更新切点位置时,只要保证鞍座顶与紧邻的吊杆之间主缆无应力长度不变,则整个主缆的无应力长度不变。以图1所示鞍座为例,圆弧AC、AD上主缆的无应力长度按照文献[1]中鞍座内主缆内力分布的模式二进行计算,即文献[1]中式(2.14)、式(2.15)。施工计算或活载加载过程当中,进行迭代求解,逐次更新切点坐标,并计算新的圆弧段上的主缆无应力长度,然后修改主缆单元CE、DF的初应变,以保证ACE、ADF这两段的无应力长度不变,直至鞍座与两边的主缆重新相切。在初应变较小的情况下,这种做法精度是很高的。

图6 索塔结构的计算图示Fig.6 Cable-tower structure schematic diagram
3 验证性算例[1]
以润扬大桥为例,按照上述方法建立ANSYS计算模型,原始数据文献[1]中算例Z5一致。不考虑主塔自重的影响,计算时未考虑桩的影响。考虑以下3个工况,比较CAP与ANSYS的计算结果。
1)工况1:塔顶鞍座的相对偏移量取1.787 5 m;
2)工况2:在工况1的基础上顶推鞍座,使塔顶鞍座的相对偏移量为1.0 m;
3)工况3:相当于成桥状态,在工况2基础上顶推鞍座,使塔顶鞍座的相对偏移量为0,并将全部荷载作用在结构上。
表1、表2、表3给出了二者控制点位置、主缆水平力和塔顶内力及无应力长度的比较。从结果来看,两者非常吻合,印证了上述方法的正确性。从塔顶内力的情况来看,两者剪力随塔顶鞍座的相对偏移量的加大而差异变大,是因为ANSYS中梁单元考虑了剪切刚度的影响,所以比 CAP中梁单元柔一些。
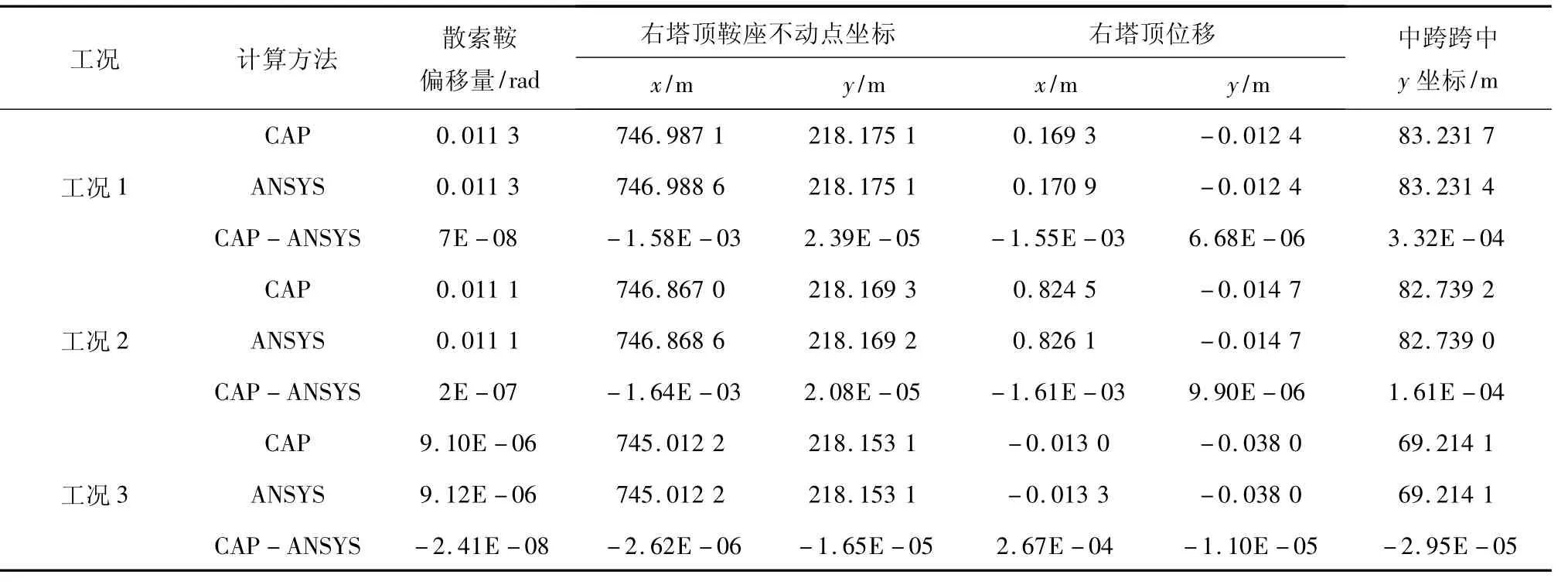
表1 控制点位置对比Table 1 Comparison of the location of control points

表2 主塔和主缆内力对比Table 2 Comparison of the tower and main cable’s internal force
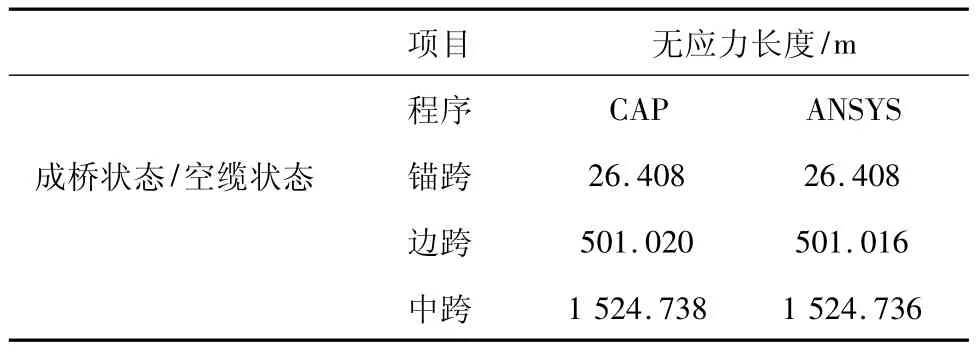
表3 无应力长度对比Table 3 Comparison of unstressed length
4 结语
1)该方法精度较高,能充分满足工程及科研精度要求。
2)该方法不需要借助于其他程序迭代出缆索无应力长或者切线角,整体性强,能够提高工作效率。
3)该方法可复制性强,参数修改也很方便,对于确定悬索桥合适的结构参数十分有利。
[1]罗喜恒.复杂悬索桥施工过程精细化分析研究[D].上海:同济大学博士论文,2004.
[2]潘永仁.悬索桥的几何非线性静力分析及工程控制[D].上海:同济大学博士论文,1996.
[3]唐茂林.大跨度悬索桥空间几何非线性分析与软件开发[D].成都:西南交通大学博士论文,2003.
[4]同济大学计算数学教研室.现代数值数学和计算[M].上海:同济大学出版社,2004.
