随机车辆荷载下三塔悬索桥钢箱梁疲劳关键断面分析
2012-07-07吉伯海
陈 策,吉伯海,刘 荣
(1.河海大学土木与交通学院,南京 210098;2.江苏省长江公路大桥建设指挥部,江苏泰州 225321)
1 前言
正交异性钢桥面系统由顶板、纵肋、横肋/横隔板等构成,出现于20世纪50年代初期。正交异性钢桥面板的整体性好、自重小,在大跨度钢桥中有着广泛的应用,已成为世界上大、中跨径现代钢桥通常采用的桥面结构形式。同时正交异性钢桥面疲劳开裂的事例已在许多国家的钢桥中出现,关于钢桥面出现疲劳开裂,最早报道出现在英国 Severn桥,1966年建成通车后,分别于1971年和1977年发现了3种焊接细节的疲劳裂纹;德国的Haseltal桥和Sinntal桥投入使用后不久,钢桥面板也都发现了疲劳裂纹。此外,日本、美国、荷兰、法国等也都发现了钢桥面板疲劳开裂事例。钢桥面板在我国使用的时间虽然不长,但是已经在一些桥中发现了钢桥面板的疲劳开裂[1~5]。这些实例表明,对钢桥面板疲劳性能进行系统研究是非常必要的。
正交异性钢桥面系统疲劳问题主要有以下几个方面原因:a.钢桥面板直接承受车辆轮荷载的反复作用;b.各部位应力影响线长度较短,一辆车经过可能会产生多个应力循环;c.钢桥面板应力状况比较复杂,并且交叉部位应力集中严重;d.U肋与横隔板角焊缝以及许多现场拼接接头的焊接质量不易保证;e.关于钢桥面板构造细节的疲劳强度数据较少,各国规范对此还没有明确规定。总体说来,正交异性钢桥面系统的疲劳性能主要取决于正交异性钢桥面顶板与U肋连接构造、正交异性钢桥面顶板U肋与横隔板连接构造两方面,直接关系到桥面系的使用寿命和安全。
泰州大桥为千米级三塔悬索桥,其结构受力特点与传统的双塔悬索桥有较大的差异[6,7]。三塔悬索桥中塔两侧主跨箱梁受力相互影响,较双塔悬索桥更为复杂,有必要对泰州大桥在车辆荷载作用下的主梁整体受力特点进行研究。
2 钢箱梁疲劳应力分析
2.1 全桥三维有限元模型
泰州大桥双主跨为1 080 m的三塔悬索桥,主梁为3.5 m高的钢箱梁,全宽39.1 m,标准段长度为16 m。主缆矢跨比采用1/9,两根主缆横向中心距离为34.8m。主塔与主梁的结构关系为:中塔与主梁之间仅设置横向抗风支座与纵向具有限位功能的弹性索,不设竖向支座;边塔处主梁设竖向支座、纵向滑动支座与横向抗风支座。
采用有限元软件ANSYS建立泰州大桥全桥有限元模型,主梁与主塔均采用beam4梁单元进行模拟,通过将主梁、主塔截面CAD图导入ANSYS中计算其截面的面积、惯性矩等参数。主缆与吊杆采用link10杆单元进行模拟,根据设计资料,将悬索与吊杆的设计索力换算为两者的初应变,在计算中形成初应力刚度矩阵。主缆与吊杆连接处的索夹采用mass21质量单元进行模拟。全桥模型的边界条件为:主缆两端6个自由度全部约束,主塔底部6个自由度全部约束,主梁与主塔根据设计资料中约束关系采用主从耦合。图1为泰州大桥的全桥有限元模型。为了模拟车辆荷载作为质量-弹簧模型在全桥结构上运行的过程,采用mass21质量单元模拟车辆重量,并通过combine14弹簧单元将质量单元与主梁进行连接。
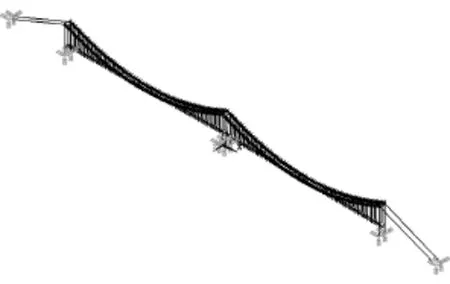
图1 泰州大桥全桥有限元模型Fig.1 Global FEM model of Taizhou Bridge
2.2 疲劳车辆荷载谱模拟
车辆荷载作用下的疲劳损伤是不断累积的过程,应采用实际的车辆作用历程作为疲劳车辆荷载谱来计算桥梁构件的疲劳损伤。通过桥梁的车流状态是一个随机过程,其车型、轴重、车重及车辆间距等随时间的变化而不同,但均服从一定的概率分布,通过Monte-Carlo法产生随机数来模拟随机车流。
基于对南京长江三桥、江阴长江大桥收费与称重系统中海量数据的处理分析,得到两座桥梁的随机车流中车重及轴重两个重要参数,将车型进行并归分类,建立典型的车型库,确定各车型所占比例,利用MATLAB统计工具箱抽取服从均匀分布的随机样本,将随机样本组合产生随机车流(见图2),将随机车流与疲劳车辆荷载模型结合,可以得到疲劳车辆荷载谱,可作为随机车流下的泰州大桥整体振动的外部荷载。
2.3 车辆荷载的简化模型
在车辆动力荷载的作用下,桥梁结构将产生振动、冲击等动力效应。在实际工程中,确定车辆荷载的简化计算模型是分析车载引起桥梁结构动力响应的关键之一。主要有三类简化的车辆荷载模型即移动荷载模型、移动质量模型与移动车辆模型,文章选用移动质量模型。假定车辆模型由两个质量组成,即刚度为Kv的弹簧支撑跳动质量Mvs和与桥梁始终保持接触的不跳动质量Mvu,如图3所示。车辆对桥梁的作用力可由式(1)表示,式(1)中,Z为弹簧质量Mvs的绝对位移,由中性位置计算。yv为弹簧质量Mvu与桥梁结构的位移。若仅考虑一阶振型,则有振型方程与弹簧上质量动力平衡方程可由式(2)、式(3)表示,式中,CB与Cv分别为桥梁与车辆系统的阻尼系数。
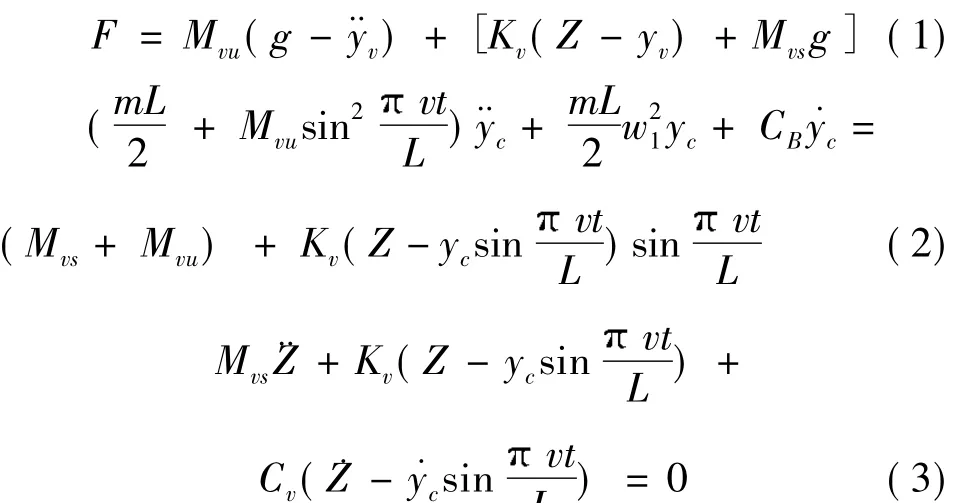
移动质量模型考虑了车辆的刚度、惯性力对桥梁结构的影响,通过在有限元中对车辆的质量及刚度进行模拟便可以实现,有利于实际工程中的运用,且影响因素考虑得相对全面。
2.4 动力响应分析
在车辆荷载作用下,主梁各部位将产生不同程度的振动响应。为了确定泰州大桥钢箱梁节段在随机车流荷载作用下应力变化敏感的位置,对主梁的位移与内力动力响应进行了研究。采用随机车流对泰州大桥全桥模型进行振动分析。计算车速采用设计车速80 km/h。
2.4.1 主梁位移动力响应
在随机车流作用下提取钢主梁左侧、右侧跨中、1/4跨、3/4跨处的位移响应,计算时程为3 min。计算结果表明,钢箱梁各截面处的竖向位移静力响应由若干个大的位移循环组成,竖向位移动力响应曲线变化趋势基本与静力响应曲线相同,且都围绕静力响应曲线小幅波动。当随机车流集中在一跨时,该跨的竖向位移响应增加明显,另一跨钢主梁向上翘曲,竖向位移响应减小,两跨间的位移响应相互影响。同时,在随机车流作用下,泰州大桥主梁左右两侧跨中的最大竖向位移分别为1.56 m、1.55 m,位移值接近。左右两侧1/4跨的最大竖向位移分别为1.42 m、0.77 m,左右两侧3/4跨的最大竖向位移分别为0.79 m、1.39 m,两侧钢箱梁在对应截面位置处的竖向位移值的差异主要是由于中塔对主梁的约束不同而引起的。
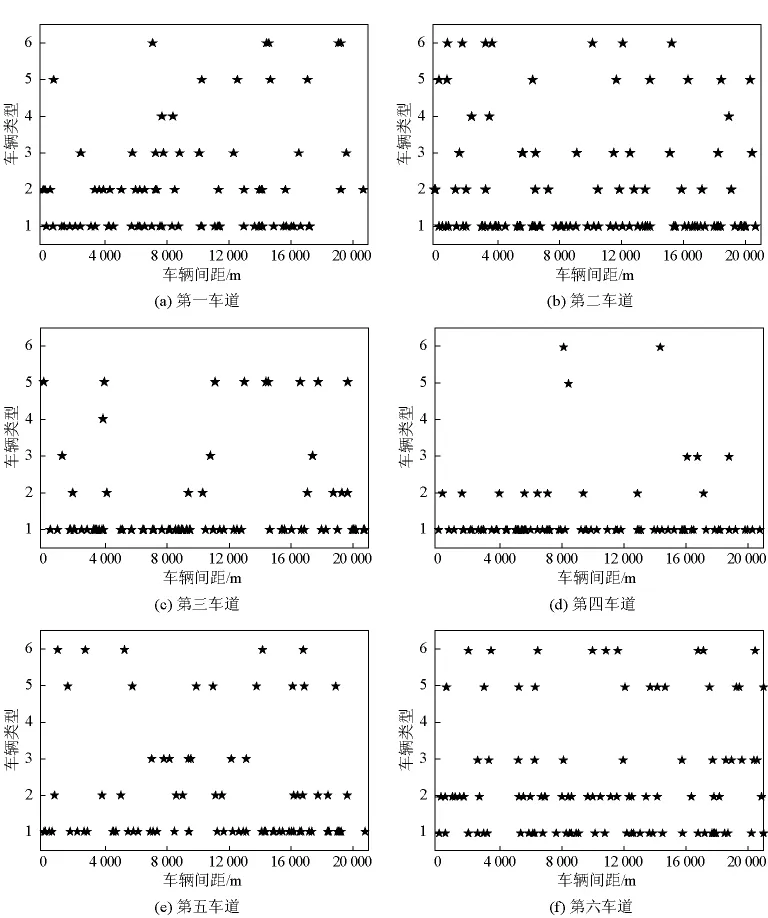
图2 江阴大桥各车道随机车流Fig.2 Random vehicle load at different driveways of Jiangyin Bridge

图3 车辆荷载移动质量模型Fig.3 Mobile quality model of vehicle load
2.4.2 主梁内力动力响应
图4为钢箱梁在对称车流作用下的弯矩响应,图中分别为左、右侧跨中、1/4跨、3/4跨处的主梁弯矩动力、静力响应。
计算结果表明,车流荷载作用下大桥主梁不同部位内力振动响应曲线总体波动趋势与静力响应曲线相似,弯矩动力响应围绕静力响应小幅波动。主梁左、右两侧的跨中位置的弯矩最大变化幅值分别为(6.19E+07)N·m、(7.45E+07)N·m。左、右侧1/4跨处的弯矩最大变化幅值分别为(4.87E+07)N·m、(7.19E+07)N·m。左、右侧3/4跨处的弯矩最大变化幅值分别为(5.80E+07)N·m、(6.49 E+07 N)·m。钢箱梁的弯矩变化是影响其应力幅的主要因素之一,以弯矩时程作为评价标准,两主跨跨中截面的疲劳受力为最不利。
3 结语
根据南京长江三桥及江阴长江大桥的实测车辆荷载数据,产生随机车流,与疲劳车辆荷载模型结合,得到疲劳车辆荷载谱作为泰州大桥整体振动的外部荷载。采用移动质量模型,将随机车流加载于全桥有限元模型上,计算泰州大桥主梁不同位置处竖向位移和弯矩的振动响应值。研究结果表明,车辆荷载下,两主跨跨中截面的疲劳受力为最不利。
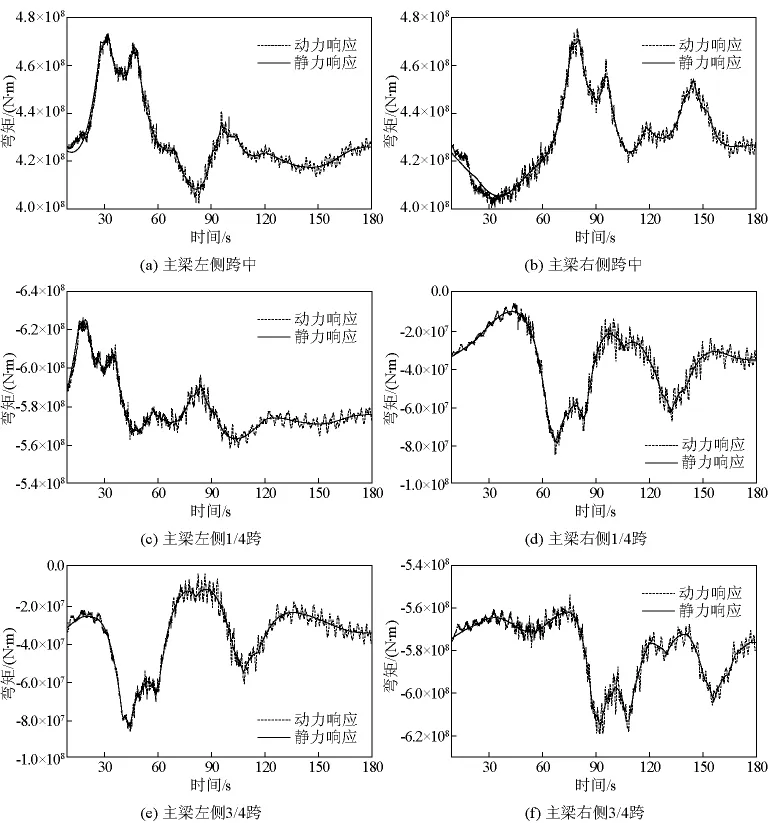
图4 对称荷载作用下主梁弯矩响应Fig.4 Bending moment response of main girder under symmetrical load
[1]Roman Wolchuk.Lessons from weld cracks in orthtropic decks on three European Bridges[J].ASCE,1990,116(1):75 -84.
[2]黄 卫.润扬长江公路大桥建设第五册:钢桥面铺装[M].北京:人民交通出版社,2005.
[3]陈惟珍,童乐为.公路钢桥疲劳与防断裂设计理论与方法研究[G].上海:同济大学桥梁工程系,2006.
[4]吴 冲.现代钢桥[M].北京:人民交通出版社,2006.
[5]项海帆.高等桥梁结构理论[M].北京:人民交通出版社,2002.
[6]陈 策.大跨径三塔悬索桥抗风性能分析[J].铁道标准设计,2008(2):30-33.
[7]陈 策,钟建驰.三塔悬索桥垂跨比变化对结构静动力特性的影响[J].桥梁建设,2008(6):12-14.
