短路限流阻抗优化配置方法研究

（浙江省电力设计院，杭州310012）

输配电技术

短路限流阻抗优化配置方法研究

丘文千

（浙江省电力设计院，杭州310012）

提出满足不同应用要求的短路限流阻抗优化配置模型，以系统短路电流方程为约束条件，以限流阻抗的取值范围和系统短路电流不超限、节点短路电流平方和最小、接入的限流阻抗代数和最小为优化目标，满足实际应用的要求。运用粒子群优化算法、遗传算法、基于广义逆与变换的优化方法以及由其构成的混合优化算法求解优化模型，提出和实现按Kuhn-Tucker条件判别优化解的最优性，通过工程实例验证了算法的有效性和实用性。

电力系统分析；短路电流；短路限流阻抗；优化算法；最优性判别

0 概述

随着我国电力系统的规模不断扩大，系统短路电流水平也不断上升，抑制短路电流超限已成为电网面临和急待解决的重大问题。为解决短路电流超限问题，可以选用更高短路容量的设备，但如果需要大量更换断路器及其它电气设备，将导致电网设施改造工作量过于巨大，不仅投资昂贵，还会影响电网的正常运行。因此，除必须更换不能满足运行要求的设备外，更多采用的是从改变电网结构、改变系统运行方式等方面考虑的限流方案，如调整电网接线、优化厂站接入方式、分层分区运行、交/直流背靠背联网、发展更高电压等级的电网、采用高阻抗主变压器或串联电抗器、主变压器中性点加装小电抗器、安装短路故障限流器等，其中优化电网结构、优化电源布局应该是首选方案，这是最根本的限流措施，但必须规划先行且有远见卓识，并解决好与运行电网的衔接。

各种短路限流方案都有一定的局限性及适用范围，并有其技术经济特点，无论采取何种方案，都应进行全面的分析比选，深入考虑其对系统的各种可能影响，根据电网的实际情况和要求择优确定。短路限流方案一般都会造成电网结构或参数的变化，大多数情况下可表示为限流阻抗的配置问题。为确定方案及参数，需要经过大量计算分析，目前主要采用常规的短路电流计算与分析方法[1-6]。为适应电网发展，需要更方便更有效的方法来进行计算，文献[7]利用阻抗矩阵支路追加公式以及短路电流与阻抗矩阵的关系式，提出由短路电流限值确定限流阻抗及其取值范围的直接方法，便于对短路限流方案及阻抗参数进行筛选和分析，但对于多变量情况不能给出最优解。遗传算法、粒子群优化算法等现代优化方法的出现推动了优化技术的发展和应用，能以较大概率趋近最优解，但趋近过程具有不确定性，可能非常缓慢。除了要提高优化效率，优化解的最优性判别也需要解决，传统优化方法也存在同样的问题。根据上述工程应用的要求，本文提出了短路限流阻抗优化配置模型及求解方法，并给出优化解的最优性判别方法。

1 短路电流计算

由于短路故障对电力系统的危害十分严重，在电力系统设计、电气设备选择、继电保护整定、运行方式编制等过程中都要进行一系列的短路电流计算，计算出在给定系统接线和参数情况下发生各类短路故障时系统各部分的短路电流。如果短路电流超过设备允许值，必须采取措施。在各类短路故障中，三相短路电流和单相接地短路电流水平反映了系统正序和零序网络特性，由于降低单相接地短路电流的有效措施更多，因此在电力系统规划设计阶段最应重视的是系统的三相短路电流水平。

常用的短路电流计算方法是应用叠加原理，将网络故障状态看成是2个网络状态的叠加，其一是故障前的网络状态，其二是网络中各发电机电势均为零，仅在故障点加一电势，该电势值与故障前的网络状态下该故障点的电压值相等，但极性相反[8]。当2个网络状态叠加时，故障点的电势值等于零。将2个网络的节点电压和支路电流分量叠加起来，就得到短路故障状态下的节点电压和支路电流。故障前网络状态的支路电流为正常的负荷电流，一般较短路电流小得多，所以简化的短路电流计算通常可忽略负荷电流的影响。简化后，短路电流计算公式如下：

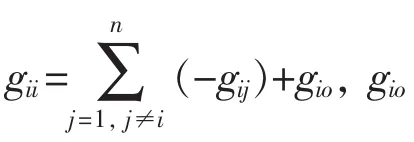
2 短路限流阻抗优化配置模型

为限制系统短路电流，在系统中接入限流阻抗，满足系统各节点短路电流不超限，实现节点短路电流平方和最小、接入的限流阻抗（或改变原设备阻抗参数产生的阻抗增量）代数和最小的优化目标，可建立如下优化模型：

在上述模型中，式（6）为目标函数项，由系统节点短路电流加权平方和及限流阻抗加权代数和组成，a1，…，an及b1，…，bm表示权重系数，用以调节各分项的影响程度；式（7）为短路电流约束条件；式（8）为的计算公式，其中的g是

ij变量xl（l=1，…，m）的函数；式（9）为限流阻抗约束条件。此模型可运用遗传算法、粒子群优化算法[9]等现代优化方法求解，这些算法不需要求导运算。

对于需要求导运算的传统优化方法，可使用如下优化模型：

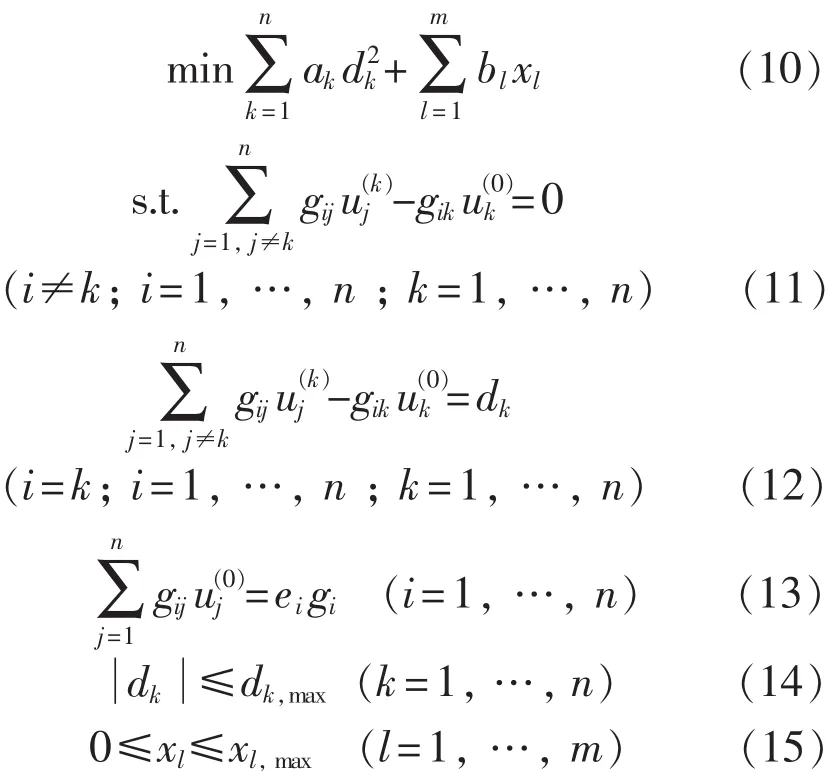
在上述模型中，式（11）-（13）为短路电流方程，式（14）为短路电流约束条件，式（15）为限流阻抗约束条件。

3 限流阻抗接入最少的优化配置模型

在实际工程中，为降低限流阻抗配置费用，要求配置数量最少，对此可给出如下优化模型：

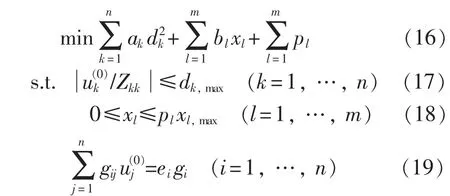
式中：pl={0，1}，pl=1表示在支路l中接入限流阻抗xl，pl=0表示不接入。

由于模型中包含了离散变量p1，…，pm，增加了问题的复杂性，受计算时间制约，对于大规模问题的求解会变得非常困难。对于含有离散变量的优化问题，运用现代优化方法求解是较合适的选择。

4 求解方法

对于优化模型（6）-（9），可采用粒子群优化算法（Particle Swarm Optimization，PSO）求解，粒子适应度函数采用罚函数法构成，即由优化模型目标函数项加上约束条件违约值的加权平方和：

PSO算法是一类基于群体智能的启发式优化方法，具有算法简单、易于实现、计算速度快等特点。计算表明，运用PSO算法求解上述优化模型能够满足工程应用要求。

一是加强政府监管。强化对工程建设全过程的质量安全监管，加强对关键工序和主要分部分项工程的验收环节的监督检查；加强对监理单位的履职情况的检查，充分发挥监理单位在质量控制中的作用；加强对工程质量检测管理，严抓建筑材料和实体结构的取样、送样检测等环节的真实性，严厉打击出具虚假报告等行为。

对于优化模型（16）-（19），可采用PSO算法或与遗传算法结合的混合优化算法[10]求解。采用PSO算法，粒子适应度函数也具有式（20）的形式，但Δf1，k（k=1，…，n）和Δf2，l（l=1，…，m）分别为约束方程（17）和（18）的违约值，对于其中的离散变量p1，…，pm，可设置门槛值，高于门槛值取1，低于门槛值取0。

对于优化模型（10）-（15），可采用基于广义逆与函数变换的优化算法[11]（Optimization algorithm based on generalized inverse matrix and function transform，OBGT）求解，也可与PSO算法构成混合优化算法。OBGT算法局部搜索能力强，但对初值敏感，而PSO算法全局搜索能力强，对初值不敏感，两类算法具有互补性。利用PSO算法的解作为OBGT算法的初值，运用OBGT算法进行二次优化，可提高收敛精度和计算速度。

5 最优性判别方法

如前所述，优化解的最优性判别问题需要解决。对于最优化问题，有：

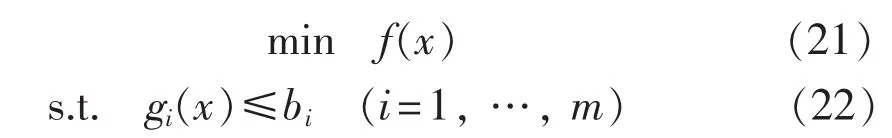
式中：x={x1，…，xn}。

式（21）、（22）最优解存在的必要条件是满足Kuhn-Tucker条件[12]：

假定已由式（21）、（22）求得优化解xopt，为运用式（23）-（26）判优须求得λi（i=1，…，m），为此引入松弛变量yi（i=1，…，m），将式（22）变换为：

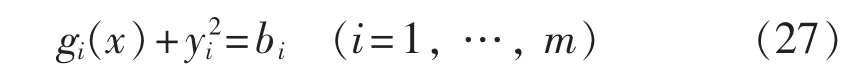
由式（24）、（27），可得：

由式（23）、（28），运用广义逆方法可得：

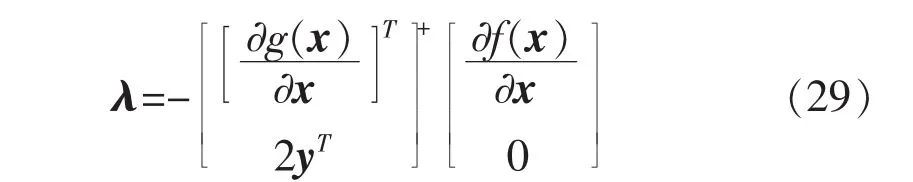
由于需要求导运算，所以优化模型需采用式（10）-（15）。

6 算例

某12节点系统阻抗参数如表1所示，支路0-1，0-2，0-3为电源支路，8-8为电抗支路，短路电流计算结果见表2，其中节点1的短路电流超过45 p.u.，节点3的短路电流超过40 p.u.。采用短路限流方案1时，各支路均可接入待选限流阻抗，其值不超过支路阻抗值的10%，各节点短路电流限制在45 p.u.内；采用短路限流方案2时，待选限流阻抗值不超过支路阻抗值的20%，各节点短路电流限制在40 p.u.内。以接入的限流阻抗值代数和最小为优化目标，结果见表1和表2，运用本文方法判定了优化解的最优性。

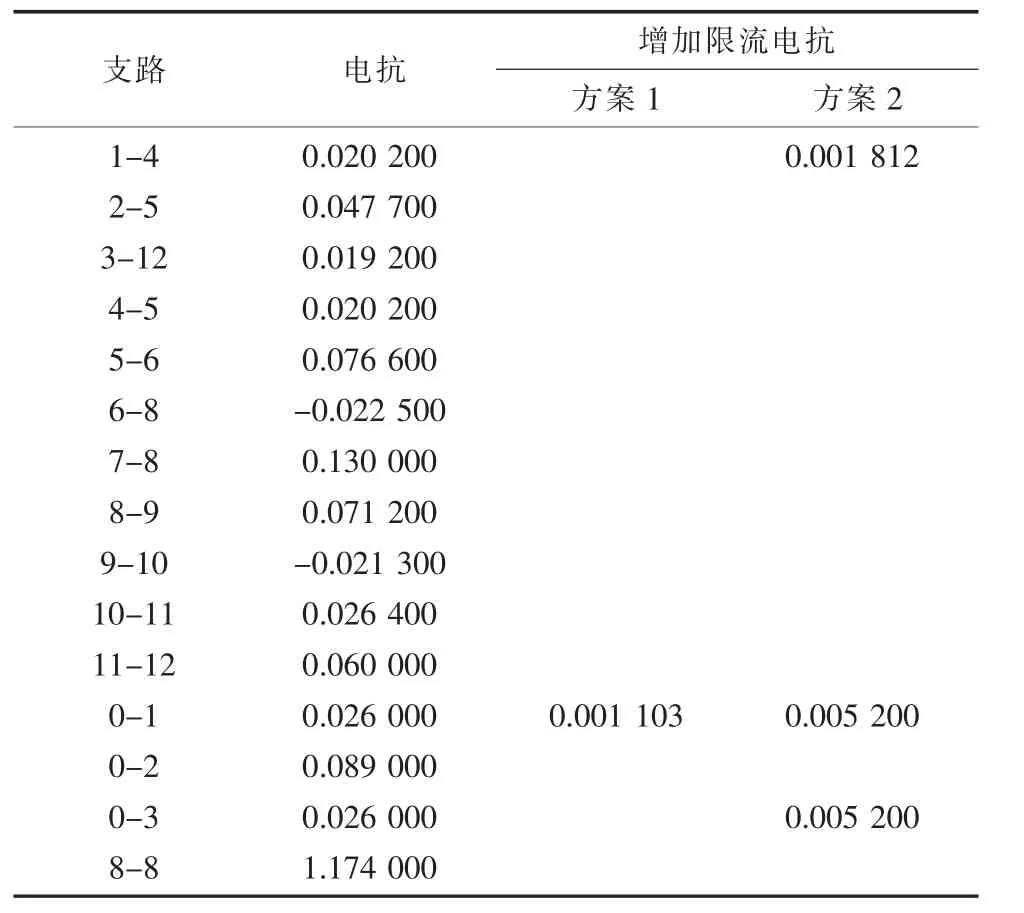
表1 12节点系统限流阻抗配置方案p.u.

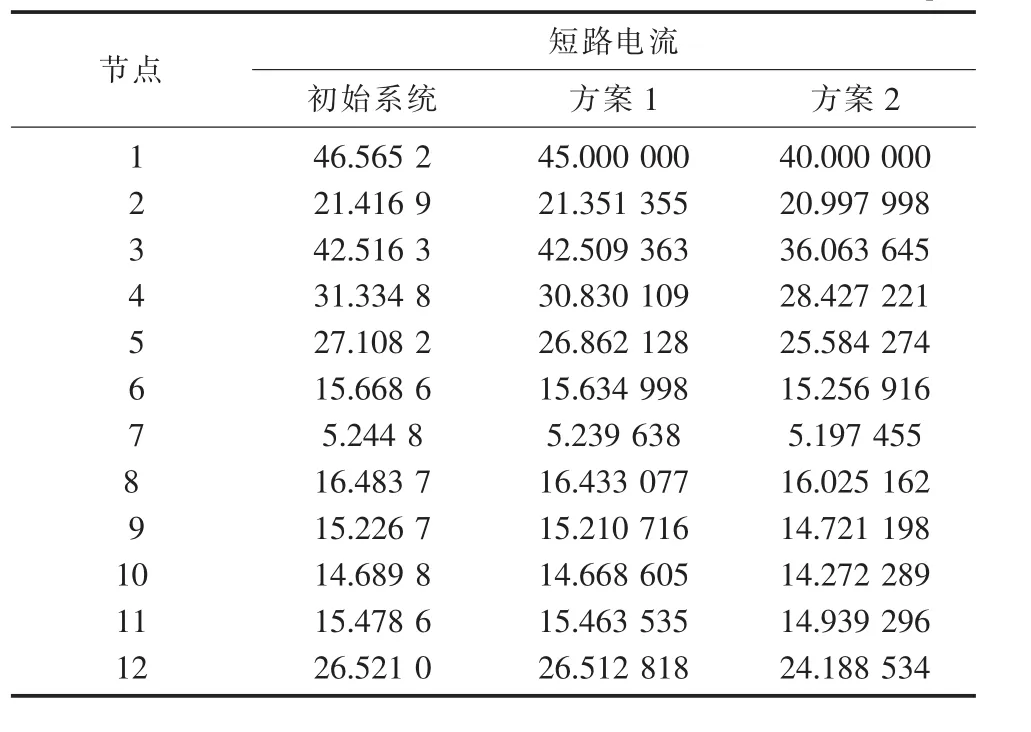
表2 12节点系统限流阻抗接入效果p.u.

某省电网规划系统，部分电网参数及短路电流计算结果如表3和表4所示，其中有7个节点的短路电流超过60 kA。采用短路限流方案1，3个变电站主变压器的阻抗百分比可由原来的18%调整为不超过24%，且变电站母线之间可装设限流电抗，各节点短路电流限制在60 kA内；采用短路限流方案2，可调整3个变电站主变压器的阻抗百分比不超过24%，变电站母线分列运行，各节点短路电流限制在60 kA内。以接入的限流阻抗值代数和最小为优化目标，结果示于表3和表4。限流方案1中，相关的9个支路均需要增加主变压器阻抗百分比或装设限流电抗，如采用限流阻抗接入个数最少的优化模型，仅需对其中7个支路调增阻抗。

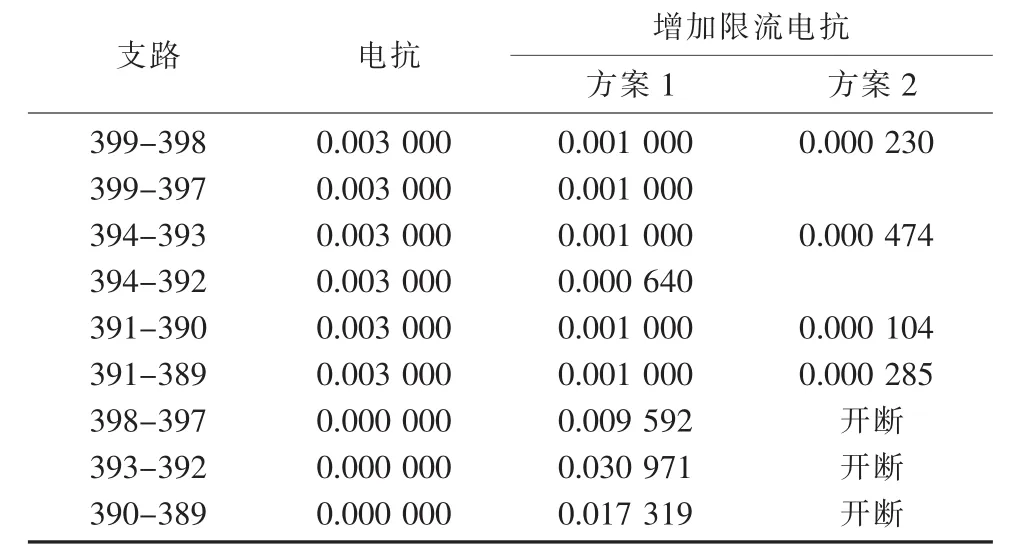
表3 电网规划系统限流阻抗配置方案p.u.

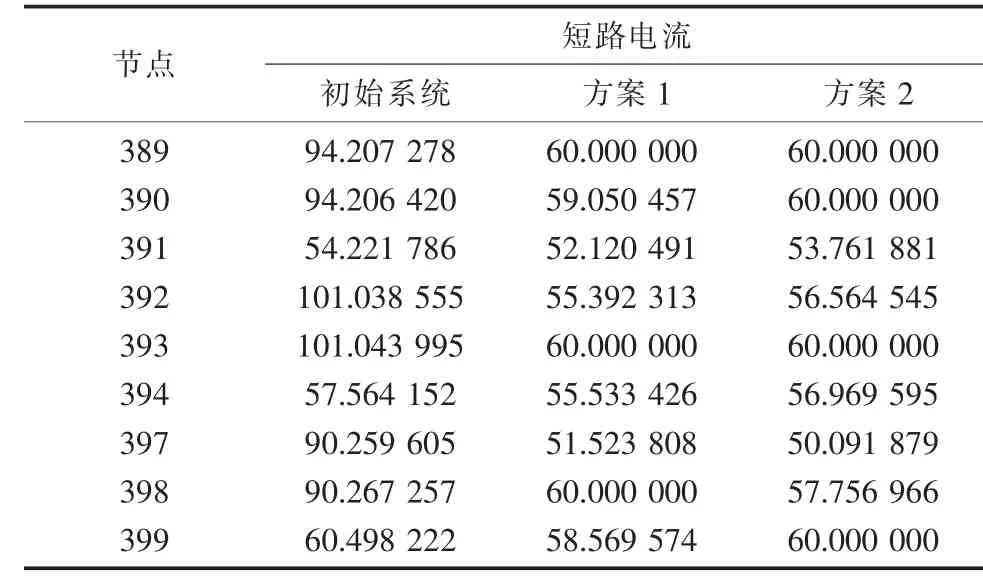
表4 电网规划系统限流阻抗接入效果kA

7 结语

确定系统短路限流方案及参数时，需要经过大量计算分析。为适应电网发展，需要更方便更有效的方法。本文提出的短路限流阻抗优化配置模型，以系统短路电流方程为约束，满足限流阻抗的取值范围和系统短路电流不超限，以节点短路电流平方和最小、或接入的限流阻抗代数和最小、或其组合为优化目标，可满足实际应用的要求。为求解上述优化模型，运用了粒子群优化算法、遗传算法、基于广义逆与变化的优化方法及其构成的混合优化算法，提出和实现按Kuhn-Tucker条件判别优化解的最优性。通过工程实例验证了算法的有效性和实用性。

[1]袁娟，刘文颖，董明齐，等.西北电网短路电流的限制措施[J].电网技术，2007，31（10）∶42-45.

[2]江林，刘建坤，周前.江苏220kV电网短路电流的分析和对策[J].华东电力，2008，36（8）∶43-46.

[3]罗纯坚，熊秀文，王冠.华中电网2010-2011年安全稳定计算分析[J].华中电力，2009，22（2）∶32-34.

[4]周惟婧，杜新伟，丁理杰.四川电网2010年短路电流水平分析及限制措施研究[J].四川电力技术，2009，32（4）∶24-27.

[5]袁智强，黄薇，江峰青.220kV电网短路电流控制措施研究[J].现代电力，2009，26（4）∶41-46.

[6]周挺，张铭.华东电网500kV短路电流限制器示范工程选点方案[J].华东电力，2008，36（10）∶44-47.

[7]丘文千．求取短路限流阻抗及取值范围的直接方法[J]．浙江电力，2009，28（6）∶1-4.

[8]西安交通大学，王锡凡．电力系统计算[M]．北京：水利电力出版社，1978.

[9]袁晓辉，王乘，张勇传，等．粒子群优化算法在电力系统中的应用[J]．电网技术，2004，28（19）∶14-19.

[10]丘文千．混合优化方法及其在电力系统无功优化中的应用[J]．中国电力，2009，42（4）∶45-48.

[11]丘文千．基于广义逆和函数变换的优化算法与应用[J]．中国电力，2010，43（1）∶30-33.

[12]M.诺顿著．现代控制理论[M]．杨志坚译．北京：科学出版社，1979.

作者简况：丘文千（1952-），男，上海人，教授级高级工程师，从事电力系统规划、工程设计与技术管理工作。

（本文编辑：龚皓）

Research on Method ofAllocation Optimization for Short-circuit Current Limiting Impedances

QIU Wen-qian
（Zhejiang Electric Power Design Institute，Hangzhou 310012，China）

The allocation optimization models of short-circuit current limiting impedances are developed to meet the demands for different applications.The models take the system short-circuit current equations as constraints to meet the optimization objective in which the value range of current-limiting impedances and system short-circuit current are within the limits and it achieves theminimum square sum of the node shortcircuit currents or theminimum algebra sum of the current-limiting impedances so as to meet the needs of practical applications.Particle swarm optimization（PSO）algorithm，genetic algorithm（GA），optimization algorithm based on generalized inverse matrix and function transform（OBGT）and the hybrid optimization algorithm combined with them are used to solve the optimization models.The method in which the optimality of model solution is judged based on the Kuhn-Tucker conditions is presented and carried out.Case studies have proved the validity and practicability of the algorithms.

power system analysis；short-circuit current；short-circuit current-limiting impedances；optimization algorithm；optimality judgment

TM744+.4

：A

：1007-1881（2012）06-0001-05

2011-11-21