油管传输射孔起爆信号的研究

闵 杰，王秀芝，刘贯虹，罗兴平，党有伟，易彩平

（陕西应用物理化学研究所，陕西 西安，710061）

油管传输射孔技术是目前国内外最为常用的射孔技术之一。对于如何判断油管传输射孔是否起爆，过去操作人员采用在井口听声音、手触摸油管感觉振动的方法，然而该方法存在不安全因素。目前，操作人员利用仪器进行安全监测，即操作人员从监测仪所采集到的各种信号中鉴别出起爆特征信号，作为判断射孔枪起爆标准。但由于操作人员的经验及各种井况的不确定性，这种被动式的操作方法存在很大的误判断性。因此，如何准确地提取出起爆特征信号，并由计算机主动进行识别判断，成为目前监测技术的一大难点。

本文通过前期自行搭建的监测实验设备，对油田实地所采集到的数据进行分析，较为准确地提取出起爆特征信号，掌握了起爆信号的一些特征参数，为后续计算机自动判断软件的编写打下基础。

1 信号处理原理

1.1 滤波

油田现场利用示波器测得的起爆特征信号及各背景噪声信号如表1所示。

表1 信号频率表Tab.1 Signal frequency

试验结果表明：起爆特征信号频率位于各个噪声信号频率的中间频段，带通滤波器具有允许特定频段的波通过同时屏蔽其他频段的波的特点，因此可以较好地从总体信号中提取起爆特征信号。

在虚拟仪器的带通滤波器选择过程中，描述实际滤波器性能的主要参数有纹波幅度d、截止频率fc、带宽B、品质因素Q以及倍频程选择性W等[1]。

理想带通与实际带通滤波器的幅频特性见图1。

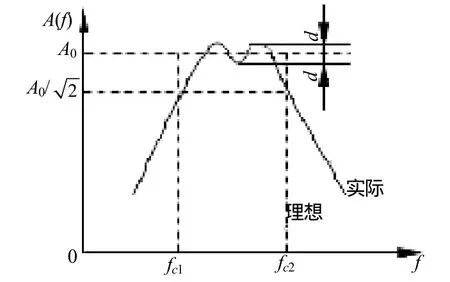
图1 理想带通与实际带通滤波器的幅频特性Fig.1 The ideal and the actual amplitude-frequency characteristics of the band-pass filter

根据起爆特征信号与噪声信号的特点，综合上述滤波器选择的主要参数，本研究采取虚拟仪器中的切比雪夫（Chebyshev）滤波器。切比雪夫滤波器是在通带或阻带上频率响应幅度等波纹波动的滤波器。切比雪夫滤波器和理想滤波器的频率响应曲线之间的误差最小，但是在通频带内有轻微的幅度波动。

切比雪夫滤波器的幅频响应为[2]：

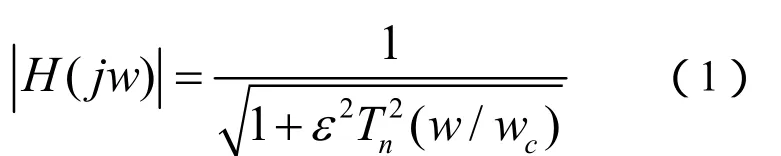
式（1）中：ε是决定通带纹波大小的系数，纹波的产生是由于实际滤波器网络中含有电抗元件；Tn是第一类切比雪夫多项式：

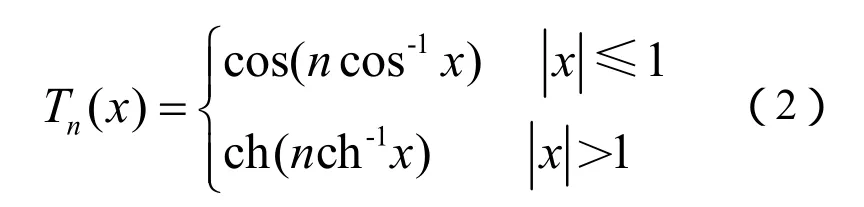
Tn特性曲线见图2。

图2 切比雪夫滤波函数特性曲线Fig.2 The characteristic curves of Chebyshev filteringfunction

从图2可以看出，在(w/wc)＜1内为通带，(w/wc)＞1为阻带。切比雪夫滤波器的幅频特性虽然在通带内有起伏，但进入阻带后衰减陡峭，更接近理想情况。在截止频率(w/wc)=1处，其衰减不一定是下降3dB，而是按来计算，ε值越小，通带起伏越小，截止频率点衰减的分贝值也越小。综上所述各方面，切比雪夫滤波器比较符合本研究的滤波需求。

1.2 短时能量

信号经过滤波处理后，还会存在一些与起爆特征信号频率相近的噪声信号，对于此种情况，需要引入短时能量分析技术。

在声波技术中短时能量分析技术用来处理同一时刻不同音源的声幅大小，它的直观意义是ΔU/ ΔT，表示在T时刻震源的能量[3]。广义地说，不同的物理量在频率上可能会一致，但造就这个物理量的能量是不一样的。井场的各种杂音信号有可能与射孔枪起爆信号处于同一频段内，但杂音的能量与射孔枪的起爆能量应不处于一个能量等级内，经短时能量分析技术处理后，可以区分是杂音信号还是射孔枪起爆信号。

短时能量的计算：设信号序列为x(i)，i= 0，M–1，则短时能量函数S(n) 定义为：

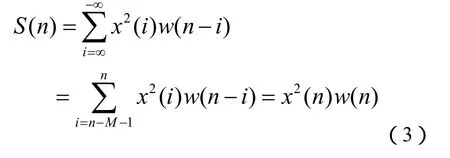
式（3）中：w(n) 为滑动窗函数，n=0，…，M-1。S(n)代表了信号在n时刻的局部能量。由式（3）可以看到短时能量分析相当于对信号先进行指数变换，然后用分段或分帧叠加的方法加以处理。分帧可以连续也可以交叠，用可移动的有限长度窗口进行加权来实现。

由于窗函数的幅频特性类似于低通滤波器，故短时能量分析也可看作是信号平方通过一个单位函数响应为w(n)的线性滤波器的输出。不同的窗函数(形状、长度) 将决定短时能量的特性，常用的窗口类型有矩形窗和海明窗。相对矩形窗而言，海明窗具有较大的带宽和较快的带外衰减速度，输入信号的失真较小，因此选用该窗函数对射孔枪起爆震动信号进行处理。当采样率一定时，窗口长度越短则时间分辨率越高，但同时又不利于发挥短时能量分析信噪比高的特点，应用中必须权衡两者加以选择。

实际信号中总是存在大量的随机噪声，相对于它的方差而言，噪声在时域中大部分时刻取值较小，少数时刻取值较大。假设在随机噪声中包含了有用的高频冲击信号，则信号经过平方处理后可以突出能量较大的有用信号，取值较小的噪声信号则可以忽略不计。又由于冲击信号具有局部连续性，在开始处连续几点的取值都较大，而噪声具有随机性，连续几点取到较大值的概率很低。所以，经过窗函数的平滑可以进一步削弱噪声的影响，从而有效地提高了信噪比，定量分析如下。

根据振动力学理论，假设振动信号满足冲击衰减振荡模型[4]：

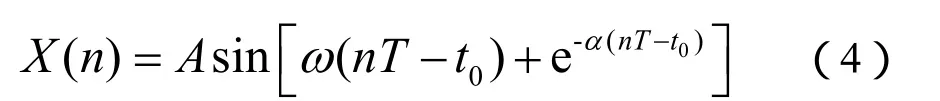
根据随机信号分析理论，如果叠加在震动信号上的噪声v(n)满足零均值高斯型随机分布，其方差为，则采样长度N足够大时噪声能量可近似表示为：

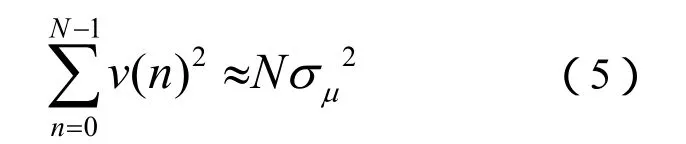
在足够长的观察时间[0，N - 1 ]，信号的总能量近似表示为：

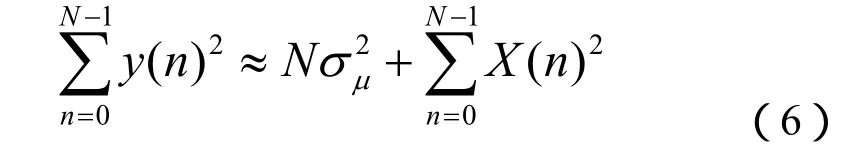
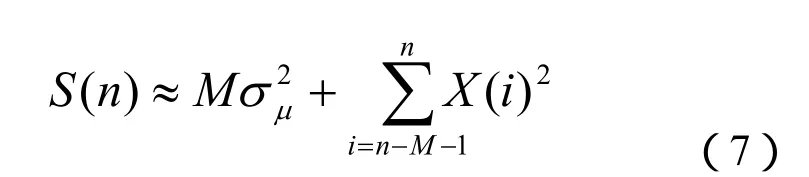
与只含噪声的短时能量相比，式（7）中增加的部分为冲击信号的瞬时能量。相对噪声而言，冲击信号在起始点的瞬时能量很大，因而用短时能量的方法可以有效提高射孔枪起爆时的局部信噪比。

2 实际信号处理分析

2.1 滤波

图3为切贝雪夫滤波器的程序设计图。

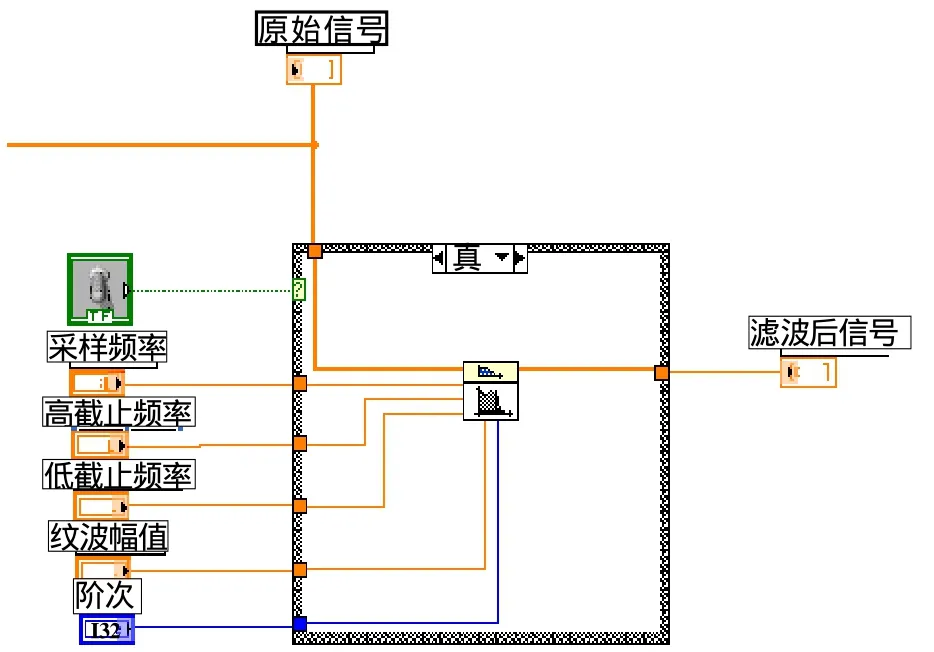
图3 切贝雪夫滤波器程序设计图Fig.3 The program design of Chebyshev filtering function

图4为普光303-2号井的监测原始数据，此口井为环空加压井，由于井口泵车打压引起的振动幅度较为强烈，再加上射孔井位较深（5 335m），因此起爆信号混杂于噪声信号之中。

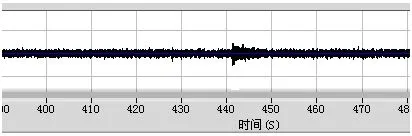
图4 普光303-2号井的监测原始数据Fig.4 The monitor raw data of Puguang 303-2 well

经过切比雪夫滤波器滤波后的效果见图5。

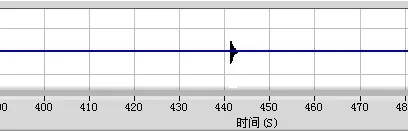
图5 经切比雪夫滤波器滤波后的数据Fig.5 The filtered data by Chebyshev filtering function

由图5可见，将信号进行带通滤波处理，可以有效地将泵车、发动机，电动机等噪声信号与起爆特征信号分离开来，便于特征信号的提取。

2.2 短时能量

图6为短时能量分析程序图。

在实际信号的短时能量处理中，海明窗的窗口长度取值是最关键的一点，因此，进行了短时能量海明窗取值实验。

胜利06-9号投棒井的井深为2 224m，当射孔枪起爆后几秒钟内，现场操作人员不慎将管钳掉落在采油树上并引起振动信号，如图7所示。

图6 短时能量程序图Fig.6 The program design of short-term energy

不同海明窗窗口长度取值下的信号处理结果见图8。

图8 不同海明窗窗口长度取值下的信号处理结果Fig.8 Signal processing results of the Hamming window with the different value

由图8可见海明窗窗口长度取值选择在30以下时，由于窗长过短，噪声信号经过处理后的幅值变大，使得特征信号与噪声信号的振幅都较大，信噪比较小；当窗长大于30时，由于窗长过长，特征信号与噪声信号相互叠加，无法区分开来。因此，本软件中的海明窗取值定为30。

某一次射孔枪起爆时的原始监测数据见图9，经短时能量分析的结果见图10。

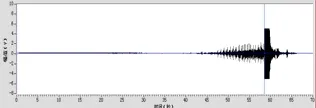
图9 原始监测数据Fig.9 The monitor raw data

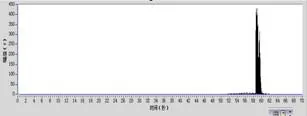
图10 短时能量处理后数据Fig.10 The processed data by short-term energy

通过对比可见，短时能量分析大大提高了信号之间的信噪比，使得起爆特征信号从与其频率相近的噪声信号中分离开来。

3 结论

（1）通过对油管传输射孔监测过程中所产生的各个信号进行特征分析，利用滤波和短时能量技术手段将不同种类的信号进行处理，达到准确提取出射孔枪起爆特征信号的目的，为后期采用软件对起爆特征信号进行自动判断打下基础。

（2）在对信号进行短时能量基础的处理中，根据实际信号的幅值及噪声的强弱，通过能量曲线图上选择合适的门限值，可得到射孔枪起爆的准确时间。

[1]刘贯虹,朱建新,张锋,周绪国.TCP监测识别系统[J].测井与射孔,2008(3):75-78

[2]郭丹枫,庞兵.振动信号处理的时频域方法[J].哈尔滨理工大学学报,2007,12(4):43-45.

[3]蒋昊,黄彬.基于LabVIEW 的振动噪声测试和分析系统开发[J].仪表技术,2007(12):28-31.

[4]朱利民,钟秉林,贾民平.振动信号短时分析方法及在机械故障诊断中的应用[J].振动工程学报,2000,13(2):400-405.