基于物元模型分析的龙凤山灌区水资源承载力综合评价
2012-07-06佟大鹏
杨 旭,佟大鹏
(黑龙江大学 水利电力学院,哈尔滨 150080)
0 引 言
水资源承载力一般是指在一定的技术经济水平和社会生产条件下水资源的最大开发容量,在这个容量下水资源可以自然循环和更新,并不断地被人们利用,造福于人类,同时不会造成环境恶化[1]。水资源承载力的研究是在可持续发展的框架下进行的,研究主要包括指标体系和评价方法,水资源承载力评价指标是关于人口、水资源、社会经济和生态环境多方面的内部特征和相互关系的综合指标,其指标体系结构是网状结构,即水资源承载力、人口、水资源、社会经济和生态环境之间,以及构成因素间都有某种关系,它们之间既互相联系又互相影响,形成错综复杂的网状结构,本文主要研究水资源承载力评价方法。目前区域水资源承载能力的评价方法主要有模糊综合评价法[2]、属性识别法[3]、系统动力学方法[4]、主成分分析法[5]、投影寻踪法[6]、神经网络[7]等。本文研究物元分析理论在水资源承载力评价中应用,物元分析理论是我国学者蔡文教授提出的[8],是研究解决矛盾问题的规律和方法,它以促进事物转化、解决不相容问题为核心,是解决多因子评价问题的比较有效的方法。本文利用该理论方法对龙凤山灌区水资源承载力进行评价,收到了满意效果。
1 物元模型原理
1.1 基本模型
给定事物的名称N,它关于特征c的量值为v,以有序三元R=(N,c,v)组作为描述事物的基本元,简称物元[8]。事物名称N,特征c和量值v称为物元的三要素。如果事物N有多个特征,它以n个特征c1,c2,…,cn和相应的量值v1,v2,…,vn描述,则表示为[9]:
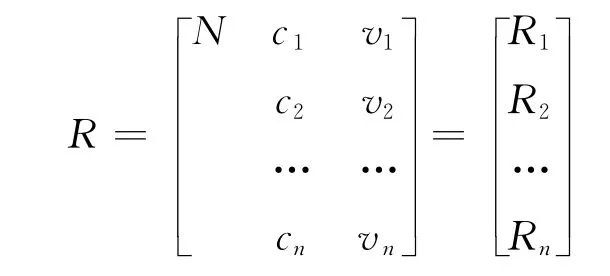
这时,称R为n维物元,简记为R=(N,C,V)。
1.2 经典域与节域物元矩阵
当N0为标准事物,关于特征ci量值范围v0i= 〈a0i,b0i〉时,经典域的物元矩阵可表示为[9]:
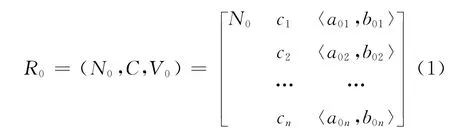
若由标准事物N0加上可转化为标准的事物所组成的物元RP称为节域物元,而vPi= 〈aPi,bPi〉为节域物元关于特征ci的比相应标准扩大了的量值范围。节域物元矩阵表示为[9]:
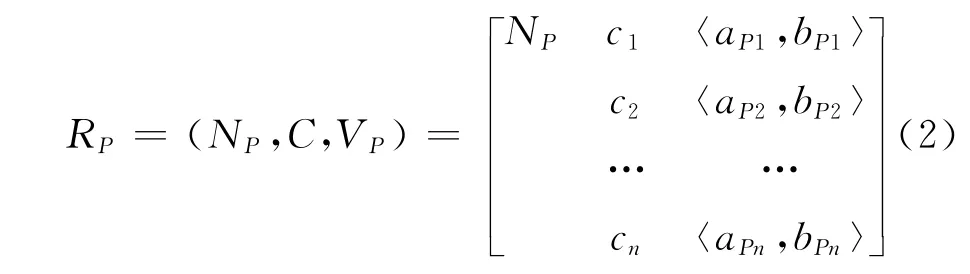
显然,这里有 〈a0i,b0i〉⊂ 〈aPi,bPi〉(i=1,2,…,n)
1.3 关联函数及关联度的计算
关联函数表示物元的量值取值为实轴上一点时,物元符合要求的范围程度。由于可拓集合的关联函数可用代数式来表达,就使得解决不相容问题能够定量化。令有界区间X0= [a,b]的模定义为:
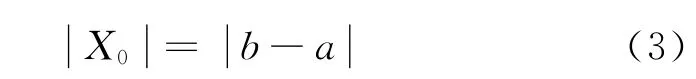
某一点X到区间X0= [a,b]的距离为:
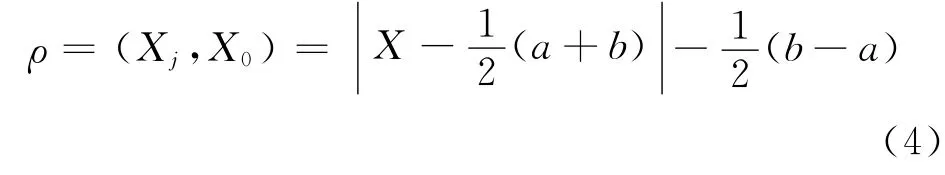
则关联函数K(x)的定义为:
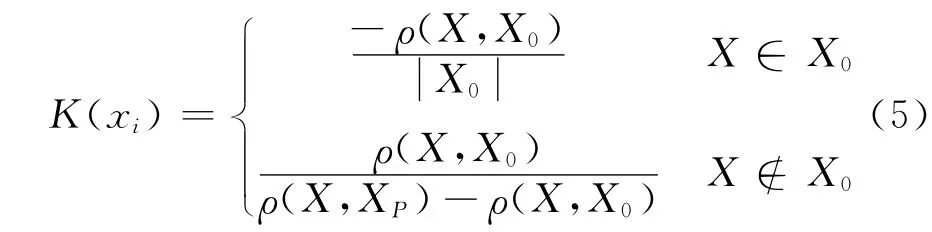
式中ρ(X,X0)表示点X与有限区间X0= [a,b]的距离;ρ(X,XP)表示点X与有限区间Xp= [ap,bp]的距离;X,X0,XP分别表示待评物元的量值、经典域物元的量值范围和节域物元的量值范围。
1.4 评价标准
关联函数K(x)的数值表示评价单元符合某标准范围的隶属程度。当K(x)>1.0时,表示被评价对象超过标准对象上限,数值愈大,开发潜力愈大;当0≤K(x)≤1.0时,表示被评价对象符合标准对象要求的程度,数值愈大,愈接近标准上限;当-1.0≤K(x)<0时,表示被评价对象不符合标准对象要求,但具备转化为标准对象的条件,且值愈大,愈易转化;当K(x)<-1.0时,表示被评价对象不符合标准对象要求,且又不具备转化为标准对象的条件。
1.5 事物的综合关联度和质量等级评定
待评事物NX关于等级j的综合关联度Kj(Nx)为[10]:
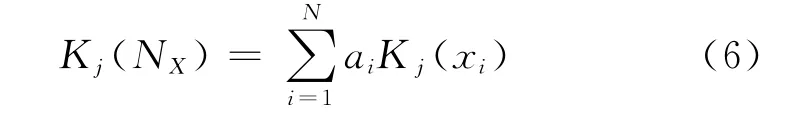
式中Kj(Nx)为待评事物关于等级j的综合关联度;Kj(xi)为待评事物关于各等级的关联度(j=1,2,…,n);ai为各评价指标的权系数。
则:

则评定事物NX属于等级j0。
2 物元模型在龙凤山灌区水资源承载力综合评价中的应用
2.1 评价因素与分级标准
影响区域水资源承载力的因素很多[11]:既有供水方面的因素,又有需水方面的因素;既有直接因素,又有间接因素。根据指标体系的完全性原则、简捷易得性原则、相对独立性原则和客观性原则,参照全面水资源供需分析中的指标体系[12]和一些关于水资源评价指标体系的研究成果[13-14]。选取了以下7个相对性评价指标。分别为:水资源灌溉率I1,水资源利用率I2,水资源开发利用程度为I3,供水模数I4,需水模数I5,人均供水量I6,渠系水利用系数I7。
1)水资源灌溉率I1:灌溉面积与总土地面积之比;
2)水资源利用率I2:75%的保证率供水量与总资源量的比值;
3)水资源开发程度I3:75%代表年的水资源开发程度;
4)供水模数I4:供给水量与土地总面积的比值;
5)需水模数I5:需水总量与土地总面积的比值;
6)人均占有水量I6:当地水资源量与总人口之比;
7)渠系水利用系数I7:进入田间的水量与渠首引水量之比。
将上述因素按对水资源承载力影响的程度划分为3个等级Ⅰ、Ⅱ和Ⅲ。Ⅰ级表示情况较好,属理想承载状态,水资源仍有较大的承载潜力,可开发利用的空间较大,水资源的供需情况较为乐观;Ⅲ级表示状况较差,属不可承载状态,表示水资源承载力已接近饱和,可利用开发的潜力较小,这时应采取相应的对策;Ⅱ级介于以上两者之间,是可承载状态,表明本区的水资源开发利用已经有相当规模,但仍有一定的开发潜力,水资源的供给对国民经济的发展有一定的保证[11]。
评价标准见表1。龙凤山灌区水资源统计情况见表2,龙凤山灌区水资源承载力的评价指标的数值见表3。

表1 综合评价指标及分级标准Table1 Comprehensive evaluated indexes and graded standard

表2 龙凤山灌区水资源统计表(p=75%)Table2 Water resources present conditions statistics of Longfengshan Irrigation District

表3 龙凤山灌区水资源评价因素的指标数值Table3 Index value of water resources evaluation factors of Longfengshan Irrigation District
2.2 水资源承载力综合评价物元模型的建立
2.2.1 确定经典物元矩阵
根据表1,取Ⅰ~Ⅲ级评价标准对应的取值范围作为经典域R01~R03。

2.2.2 确定节域物元
根据表1和表3中评价因子的取值范围来确定节域RP。
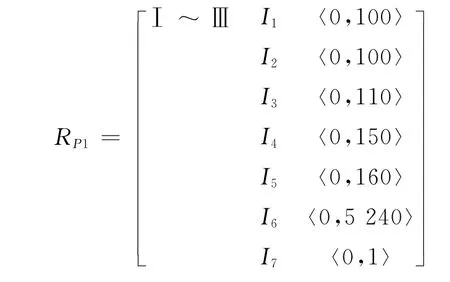

2.2.3 计算权系数
对于评价等级Ni(i=1,2,…,m)门限值Xij的权系数(表4)为:
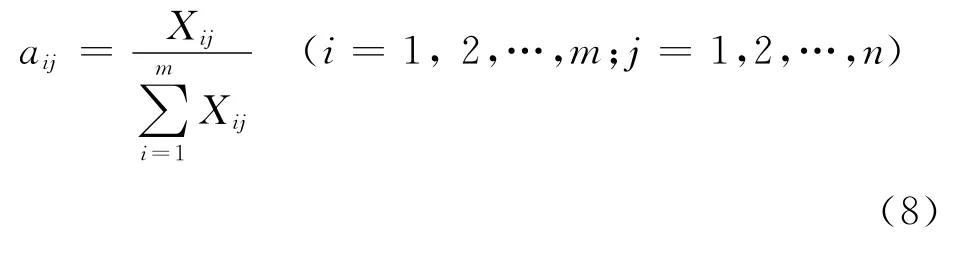
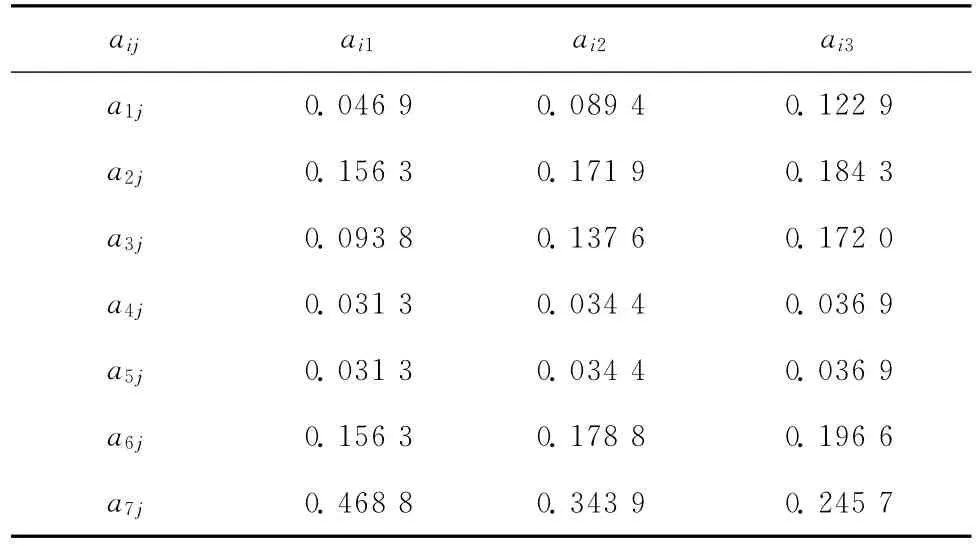
表4 权系数表Table4 Weight coefficient
2.2.4 综合关联度计算及评价结果
根据式(4)、式(5)、式(6)计算龙凤山灌区的综合关联度,综合关联度及评价结果见表5。

表5 综合关联度及评价结果Table5 Comprehensive correlation and evaluation results
3 结 论
利用综合关联度越大,则评价事物属于该等级的物元模型评价原理[15],由式(7)及综合关联度及评价结果可得出龙凤山灌区2009,2015年和2025年水资源承载力均属于Ⅱ级,说明灌区水资源开发利用已有相当规模,但仍有一定的开发潜力,可以采用相关工程措施进一步开发水资源。
以上物元分析理论方法应用表明:该计算方法简便,评价结果符合实际情况,利用该方法综合评价灌区水资源承载力是合理可行的,并且关联函数可以取负值,其评价结果更能全面反映评价对象是属于某一等级的程度,评价结果更为精确,为该灌区水资源开发利用提供理论依据和支持。
[1]付 强.农业水土资源系统分析与综合评价 [M].北京:中国水利水电出版社,2005.
[2]闵庆文,余卫东,张建新.区域水资源承载力的模糊综合评价分析方法及应用 [J].水土保持研究,2004,11(3):14-16.
[3]李恩宽.属性识别模型在水资源承载能力评价中的应用 [J].人民黄河,2008,30(3):45-47.
[4]孙新新,沈 冰,于俊丽,等.宝鸡市水资源承载力系统动力学仿真模型研究 [J].西安建筑科技大学学报:自然科学版,2007,39(1):72-77.
[5]周 琳,金 辉.主成分分析法在江门市水资源承载力研究中的运用 [J].人民珠江,2007,(5):39-42.
[6]赵小勇,付 强.投影寻踪模型的改进及其在城市水资源承载能力预测中的应用 [J].数学的实践与认识,2007,37(7):76-81.
[7]陈守煜,李庆国.一种新的模糊聚类神经网络及其在水资源评价中的应用 [J].水利学报,2005,36(6):662-666.
[8]蔡 文.物元模型及其应用 [M].北京:科学技术文献出版社,1994.
[9]林 晖.基于物元分析的地下水质量综合评判 [J].能源与环境,2011,(4):26-30.
[10]蒋慧云,吕惠进,李佐卿,等.水质评价的物元分析模型 [J].广东农业科学,2012,(2):148-150.
[11]付 强.数据处理方法及其农业应用 [M].北京:科学出版社,2006:1-164.
[12]施嘉炀.水资源综合利用 [M].北京:中国水利水电出版社,1995.
[13]左东启,戴树声,袁汝华,等.水资源评价指标体系的研究 [J].水科学进展,1996,7(4):367-373.
[14]张丽萍,朱钟麟,邓良基.水资源评价指标体系的研究现状及问题探讨 [J].国土资源科技管理,2004,21(4):5-9.
[15]杨 广,何新林,李俊峰,等.基于物元模型的干旱区水资源承载力评价研究 [J].人民长江,2009,40(21):52-54.
