反馈鲁棒H∞控制器的存在条件

李晶晶

（山东科技大学理学院 山东 青岛 266590）

1 简述(Simple Description)

时滞现象是自然界中普遍存在的现象,在控制系统的设计和分析中如不考虑时滞的影响，有可能导致闭环系统的不稳定。因此近年来时滞系统的研究已经成为控制领域一个非常热门的研究方向[1-3]，H∞控制是一种重要的鲁棒控制方法，它要求在系统存在不能精确测量的外部干扰情况下，设计控制器有效抵消外来干扰的影响在一定水平之下。H∞控制无论在理论研究还是工程应用方面都取得了巨大的进展。纵观现有文献，当系统方程中含不确定项，状态和控制同时有时滞情形，其相关的H∞控制研究几乎还是个空白。本文对状态和输入带时滞的不确定性线性系统，利用线性矩阵不等式LMI（Linear Matrix Inequality）[4]的处理方法，给出了状态反馈鲁棒H∞控制器存在的条件。本文所设计的状态反馈控器能够使时滞系统不仅对参数不确定性具有鲁棒性而且对外部扰动满足给定的衰减性能指标。

2 问题描述(Problem Description)

考虑不确定线性时滞连续系统：

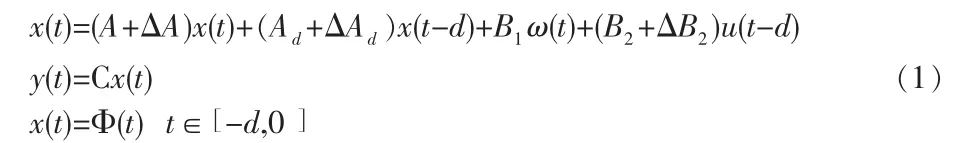
其中 x(t)∈Rn为状态变量，u(t)∈Rm为控制变量，ω(t)∈Rn为有限能量的外部干扰，y(t)为被调输出变量，时滞d≥0。

假设参数不确定性满足匹配和范数有界条件：

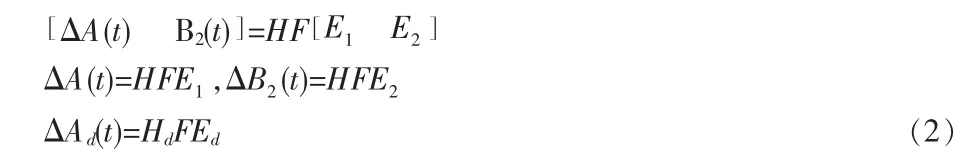
式中：H，Hd，E1，E2，Ed为适维常值矩阵，F(t)为时变适维 Lebesgue可测函数矩阵，且满足

若采用无记忆状态反馈控制

则闭环系统为：

本文的问题描述是：对不确定时滞连续系统（1），给定H∞干扰衰减指数r，如何求出状态反馈控制（3），对任意d≥0满足：

⑴闭环系统是渐近稳定的;

⑵ 从外部干扰ω(t)到输出y(t)的传递函数矩阵G(s)的H∞范数不超过给定的常数r，即在零初始条件x(t)=0，t∈［-d, ］0 时：

其中，r是一预先规定的常数。

如果满足上述条件的状态反馈控制器（3）存在，称系统（1）在状态反馈控制器（3）的作用下是具有H∞范数界r可靠鲁棒镇定的。

3 主要结果(Main Conclusion)

引理1[1]对如下线性时滞系统：

若存在对称正定矩阵，使下列矩阵不等式成立：

则系统（6）具有性能 r。

引理2[2]对任意矩阵M，H和E为合适维数的实矩阵，且对于所有的 F(t)满足 F(t)TF(t)≤I，我们有

M+HF(t)E+ETF(t)THT＜0

当且仅当存在常数ε＞0，使得：

M+εHHT+ε-1ETE＜0

引理 3[3]（schur’s 补引理）：实矩阵 N，M=MT，R=RT＞0,下列两个式子是等价的：

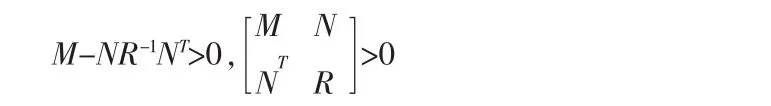
定理1对系统（1）和给定的干扰衰减指标r＞0，使得对所有允许的不确定性F（t），如果存在对称正定矩阵X，Q和矩阵W，以及标量ε1＞0,ε2＞0，使得以下矩阵不等式成立：

则系统（1）存在具有H∞性能r的无记忆状态反馈鲁棒控制器。若（）是矩阵不等式（8）的一个可行解，则是系统（1）的一个状态反馈鲁棒H∞控制器。

证明:要使系统（1）具有H∞性能指标r，根据引理1，须有下列不等式成立：

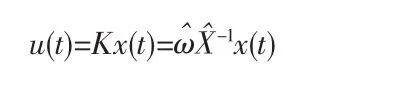
根据引理[2]，式（9）成立，当切仅当存在标量 ε1＞0,ε2＞0，使得下式成立：

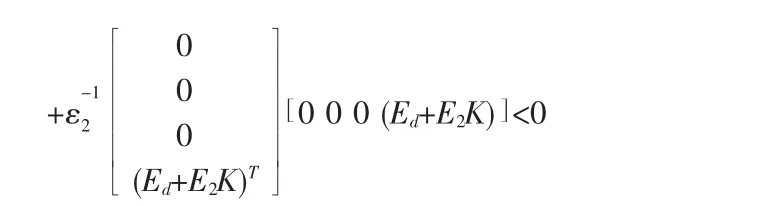
将y1代入，利用Schur补性质，有：

再利用Schur补性质，有：

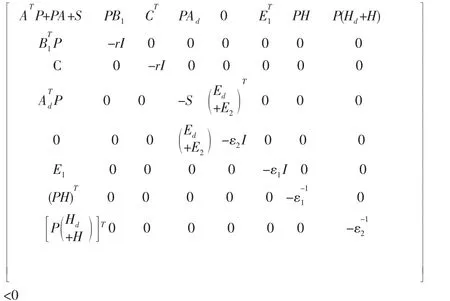
其中，X=P-1W=KP-1Q=P-1SP-1

从而定理得证。

4 结论(Conclusion)

针对状态和输入带时滞的不确定性线性系统，利用线性矩阵不等式LMI（Linear Matrix Inequality），提出了反馈鲁棒H∞控制器的存在条件。本文所设计的状态反馈控器能够使时滞系统不仅对参数不确定性具有鲁棒性而且对外部扰动满足衰减的性能指标。

［1］Zhang,W.H.,Chen,B.S.,Feedback stabilizability of nonlinear stochastic systems with state and control-dependent noise[M].The 4th Asian Control Conference,2002,to appear.

［2］Mao,X.,Robustness of exponential stability of uncertain stochastic differential delay equations[M].System&Control Letters,35,325-336,1998.

［3］何关珏.线性控制系统理论[M].沈阳:辽宁人民出版社，1982.

［4］程云鹏,张凯院,徐仲.矩阵论[M].西安:西北工业大学出版社，2002.