空间差值在渤海海水污染面积评估应用研究
2012-07-06尹维翰齐衍萍樊晓杰
尹维翰 齐衍萍 樊晓杰
(1.国家海洋局北海环境监测中心 山东 青岛 266033;2.国家海洋局海洋溢油鉴别与损害评估技术重点实验室 山东 青岛 266033;3.中国海洋大学海洋地球科学学院 山东 青岛 266100)
空间插值作为一项基本的空间分析技术,已开始应用于海洋环境评价领域,从基础的海洋环境因子等值线和等值面图的绘制,到建立在插值平面基础上的环境因子时空变化分析[1]、环境综合评级[2]、海洋系统动力学模型等等。目前已成为海洋海洋环境评价不可或缺的工具之一,但它也是海洋环境评价中的薄弱环节。在多数的研究中,也并不重视进行插值方法的筛选和差值参数的优化。使用不合适的方法或参数,会造成严重的插值噪音,使变化趋势难以辨识,甚至会产生扭曲的变化趋势,误导推理和判断,产生错误的决策结果[3]。
插值方法的筛选、条件的优化已经成为空间差值技术在各领域应用研究的热点,在气象、土壤、遥感等领域都有广泛报道,但在海洋环境评价领域研究甚少。李峋曾利用高维空间插值在海洋环境数据预处理中的应用进行了研究,而针对海洋环境污染面积评估研究还未见有报道。因此,本文利用渤海海洋环境监测资料,在探索性空间数据分析和数据转化的基础上,分别使用3种方法对渤海各类水质面积进行插值,最后对各项优化措施效果进行验证,为海区海水污染面积评估提供了理论依据,为海洋行政主管部门提供了有力的技术支撑。
1 数据来源
国家海洋局北海分局 2010 年在渤海区(〈121.1630E,38.7370N〉和〈120.8690E,37.8240N〉两点连线以西的渤海海域)监测任务。

图1 渤海海域监测站位分布
监测站位如图1所示。监测采样和样品分析均按照《海洋监测规范GB 17378-1998》来进行。
2 空间数据分析讨论
检验数据的正态分布性是使用空问统计学变异函数计算和克立格法进行土壤质量空间分析的前提,只有当数据服从正念分布时,空间插值才有效。对不符合正念分布的变量数据进行对数转换后再进行检验。目前,国内常用的方法有单样本K-S检验和多样本的Q-Q图检验和直方图检验。K-S检验是利用样本数据推断总体是否服从某一理论分布,因其主要用来做单样本数据探讨,本文不做进一步讨论。
Q-Q图和直方图均是通过观察数据的效果图来判断数据是否服从正态分布。Q-Q图是其横坐标为改变量的观测值,纵坐标为位数。若该组数据服从正态分布,则图中的点应该形成近似y=x直线。非标准正态分布的斜率为样本标准差,截距为样本均值。直方图又称质量分布图、柱状图,它是表示资料变化情况的一种主要工具。用直方图可以解析出资料的规则性,比较直观地看出产品质量特性的分布状态,对于资料分布状况一目了然,便于判断其总体质量分布情况。不难看出,此两种方法均依靠主观观察来鉴别样品数据是否符合正态分布,人为因素往往会导致错误的判断,如图2所示,直方图直接观测数据应该符合正态分布,但经检验AD=1.1>1,实为非正态分布。
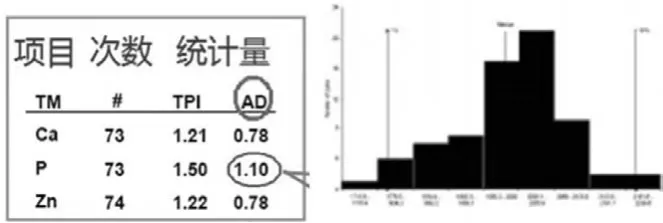
图2 直方图正态分布检验
基于此,本文推荐采用Anderson-Daeling检验,该检验是Anderson-Daeling1954年提出的检验统计量A*,以此来度量经验分布函数与总体分布函数的偏离程度:
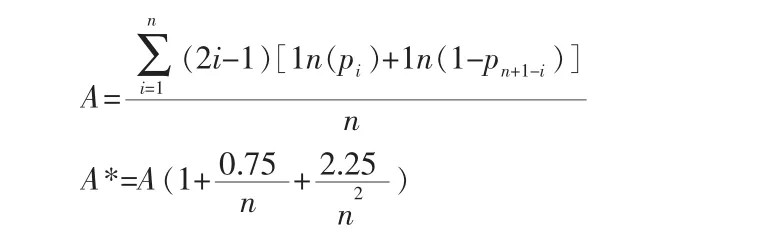
若A*<1,则样本数据符合正态分布。该方法功效随样本容量的增大而增大,随显著性水平的提高而增大[4]。
3 空间差值分析
根据海洋环境因子的空间变异性对环境因子的空间插值技术进行了分析比较,以选出一种适合的插值算法处理评价结果,使输出面的灰度数值分布的失真度为最小,确定拟合较优的插值方法。
3.1 IDW反距离加权法
反距离加权法是一个加权平均插值法,可以进行确切的或者圆滑的方式插值。方次参数控制着权系数如何随着离开一个格网结点距离的增加而下降。对于一个较大的方次,较近的数据点被给定一个较高的权重份额,对于一个较小的方次,权重比较均匀地分配给各数据点。计算一个格网结点时给予一个特定数据点的权值与指定方次的从结点到观测点的该结点被赋予距离倒数成比例。
3.2 Spline 条样法
样条函数是使用函数逼近曲面的一种方法。样条内插的本质是利用数学方法产生一组已知采样点的平滑曲线,并依据这条曲线来估计每个点的属性数据值,在计算过程中要求通过已知样本点的曲面的曲率最小。理论上采用高阶多项式进行插值估计可以得到高阶平滑结果,但实际研究中较多采用二阶多项式估值。
3.3 Kriging算法
克里金插值法以空间自相关为基础,利用区域化的变量的原始数据和变异函数的结构特点,对未知点的区域化的变量进行线性无偏最优估计的一种插值。具体地说克里格插值要求所有点属性值服从正态分布。更详细的讲,克里金法是根据未知点有限邻域内的若干已知点的测量值关系,与未知样本点相互空间位置关系,以及变异函数提供结构信息之后,对未知点值进行的一种线性无偏最优估计。
3.4 算法比较
样条函数不需要对空间结构进行预先估计和作统计假设,只进行局部区块的拟合,但作为一种函数方法,难以满足对于利用有限的观测数据进行缺值预测和内插格网的精度要求,也难以对误差进行估计,样本点稀疏时插值效果不好。
反距离加权法计算开销少,具有普适性,不需要根据数据的特点对方法加以调整。但其作为一种几何方法,插值结果受r值的影响很大,根据不同r值估算的同一未知点的值会有很大的差别。当任何一个曲卸(1≤i≤n,1≤r≤n)时,该点权值为无穷大,导致该点的输出数据不连续,计算时会得到其实际测量值,在进行外插值时,反距离加权法会不恰当地将这些估计直回归为观测数据的平均值。
克里金插值法以空间统计学作为理论基础,可以克服内插中误差难以分析的问题,能够对误差作为这逐点的理论估计,不会产生回归分析的边界效应,插值精度较高,唯一性很强,外推能力较强。克里金插值的不足时做为一种地统计学方法,复杂,计算量大,运算速度慢,需要较高配置的高性能计算机,但其已经作为最重要的插值方法在GIS领域中得到应用。
对3种插值方法的插值中误差进行比较,存在较大差异,在进行不均匀分布数据中,克里金插值法可以得到了较好的精度结果,因此本文推荐选用克里金插值法作为渤海海水污染面积评估的插值方法[5]。
4 结论与建议
对单样本K-S检验和多样本的Q-Q图检验和直方图检验以及Anderson-Daeling检验研究表明,Anderson-Daeling检验更适合海洋环境监测领域中的多样本数据空间转化分析和正态分布检验,且该方法能够较客观的反应数据本质,受人为主观影响较小。
对三种插值方法的研究表明,克里金插值法更适合渤海海域污染面积评估中应用。从海洋环境研究角度讲,它根据已知监测站位点上环境要素变量,如某种污染物浓度的实测数据,对环境要素变量进行结构性(变差函数模型的确定)分析之后,为了对待估点做出一种线性、无偏、最小方差的估计,而对周围已知站位点的测量值赋予一定权系数,进行加权平均来估计待估点环境要素变量的方法。
因海洋的流动性、边界的不确定性,生物地球化学循环等复杂性等,空间插值分析如何在海洋环境监测领域应用需进一步研究。
[1]蔡文贵,贾晓平,李纯厚.基于GIS的粤西海域浮游植物的时空变化分析[J].生态学报,2004,24(100):2143-2148
[2]蔡文贵,李纯厚,林钦,等.粤西海域饵料生物水平及多样性研究[J].中国水产科学,2004,11(5):440-446.
[3]Mitas L,Mitasova H.Spatial interpolation methods in GIS.In:Longley P A ed.Geographical information system.Volume 1,principles and technical issues,second edition[J].New York:Join Wiley&Sons,1999:452-461.
[4]章刚勇,阮陆宁.基于Monte Carlo随机模拟的几种正态性检验方法的比较[J].统计与决策,2011,4(7):17-20.
[5]刘光孟,汪云甲,张海,等.空间分析中几种插值方法的比较研究[J].地理信息世界,2011,8(3):41-45.
