关于丢番图方程(12n)x+(35n)y=(37n)z

杨志娟,翁建欣

(安徽师范大学数学系,安徽 芜湖 241003)

关于丢番图方程(12n)x+(35n)y=(37n)z

杨志娟,翁建欣

(安徽师范大学数学系,安徽 芜湖 241003)

运用同余及元素阶的性质,证明对任意正整数n,丢番图方程

仅有正整数解(x,y,z)=(2,2,2).

Je´smanowicz猜想;丢番图方程;同余

1 引言

2 引理及定理 4的证明

致谢感谢导师汤敏教授在论文撰写过程中给予的精心指导.

[1]Sierpi´nski W.On the equation 3x+4y=5z[J].Wiadom.Mat.,1955/1956,1:194-195.

[2]Je´smanowicz L.Several remarks on Pythagorean numbers[J].Wiadom.Mat.,1955/1956,1:196-202.

[3]Deng Moujie,Cohen G L.On the conjecture of Je´smanowicz concerning Pythagorean triples[J].Bull.Aust. Math.Soc.,1998,57:515-524.

[4]Le Maohua.A note on Je´smanowicz conjecture concerning Pythagorean triples[J].Bull.Aust.Math.Soc., 1999,59:477-480.

[5]关文吉.关于商高数的Je´smanowicz猜想[J].纺织高校基础科学学报,2011,24(4):557-559.

[6]Yang Zhijuan,Tang Min.On the Diophantine equation(8n)x+(15n)y=(17n)z[J].Bulletin of the Australian Mathematical Society,2012,86(2):348-352.

[7]陆文端.关于商高数组4n2−1,4n,4n2+1[J].四川大学学报:自然科学版,1959,2:39-42.

On the Diophantine equation(12n)x+(35n)y=(37n)z

Yang Zhijuan,Weng Jianxin
(School of Mathematics and Computer Science,Anhui Normal University,Wuhu 241003,China)

Using the properties of congruences and the order of elements,we show that,for any positive integer n,the Diophantine equation(12n)x+(35n)y=(37n)zhas no solution other than(x,y,z)=(2,2,2)in positive integers.

Je´smanowicz conjecture,Diophantine equation,congruence

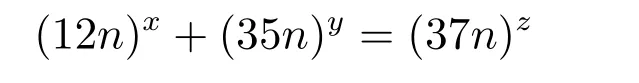
O156

A

1008-5513(2012)05-0698-07

2012-05-14.

国家自然科学基金(10901002);安徽省自然科学基金(1208085QA02).

杨志娟(1987-),硕士生,研究方向：组合数论.

2010 MSC:11D61