一类混合单调算子方程的求解及应用

田杰

(西北大学数学系,陕西 西安 710127)

一类混合单调算子方程的求解及应用

田杰

(西北大学数学系,陕西 西安 710127)

利用锥理论和半序方法证明了Banach空间中一类非线性二元算子方程的解的存在唯一性定理,并给出迭代序列收敛于解的误差估计,作为应用,讨论了不具有单调性的算子方程的可解性,改进并推广了已有的一些结果.

算子方程;迭代求解;锥理论

1 引言

利用锥理论研究了Banach空间中一类单调混合算子方程A(x,x)=(1+α)x解的存在唯一性问题,混合单调算子是一类重要的算子,1987年由郭大钧教授及Lakshmikantham提出,现已有一批好的结果[14].本文对算子的连续性和紧性不作任何假定,并给出迭代序列收敛于解的误差估计,推广了现有文献的一些结论.

设E为Banach空间,P⊂E为锥,P在E中导出一个半序“≤”,关于锥和由锥导出的半序的详细内容请参看文献[5].θ表示E中的零元素.

2 主要结果

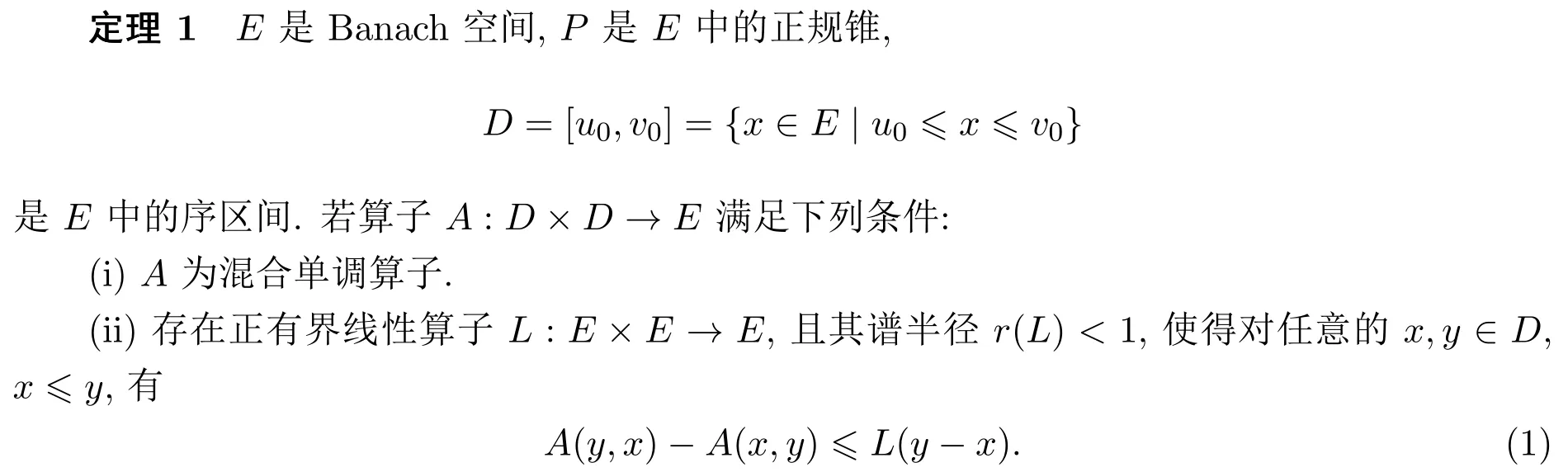
3 应用

注 2本文给出的混合单调算子方程的求解方法,改进了文献[7]的相应结果,并加强了其结论.

[1]孙经先,刘立山.非线性算子方程的迭代求解及其应用[J].数学物理学报,1993,13(2):141-145.

[2]孙经先.一类非线性算子方程的迭代求解.工程数学学报[J].1989,6(2):12-17.

[3]谷峰.一类非线性算子方程解的迭代逼近[J].纯粹数学与应用数学,1999,15(2):93-98.

[4]张庆政.序对称压缩算子方程的迭代求解及其应用[J].工程数学学报,2000,17(2):131-134.

[5]Taylor A E,Lay D C.Introduction to Functional Analysis[M].New York:Springer-Verlag,1980.

[6]孙经先.非线性泛函分析及其应用[M].北京:科学出版社,2008.

[7]李俊强,张裴然.一类混合单调算子的新不动点定理得推广[J].郑州大学学报,2004,46(4):13-15.

Iterative solution of some mixed monotone operators equation and applications

Tian Jie
(Department of Mathematics,Northwest University,Xi′an 710127,China)

By using the cone theory and partial technique,the existence and uniqueness theorem of solutions for a class of nonlinear binary operator in Banach spaces are investigated,and the error estimates that iterative sequences converge to solutions are also given.As the applications of the resulting results,the solvability of operator equations which do not possess monotonicity are discussed.The results presented here improve and generalize some known results.

operator equation,iterative solution,cone theory

O177.91

A

1008-5513(2012)05-0692-06

2012-01-09.

陕西省自然科学基金(2012JM1017).

田杰(1987-),硕士生,研究方向：非线性泛函分析.

2010 MSC:47H10