数字电源模糊自适应PID控制算法仿真研究

张小庆，彭彧华，唐小英，刘伟峰

（北京理工大学生命学院，北京 100081）

相比较于传统的开关电源，数字电源具有设计周期短，控制方法灵活，易于实现模块化管理，能够消除因离散元件引起的不稳定和电子干扰的特点[1]，所以数字电源是开关电源的一个发展趋势。数字电源的控制模块对数字电源的性能有着重大的影响，目前数字电源的控制方法一般采用简单的数字PID控制算法。但是，传统的PID算法是一种线性控制算法，在控制数字电源这种非线性系统时动态性能不佳，主要体现在负载变化或者有干扰的情况下，电源输出超调大，调节时间长等方面。模糊控制是应用模糊集合理统筹考虑系统的一种控制方式，即使在不精确知道系统的数学模型的情况下也能够对系统进行有效的控制[2]，并且具有上升时间快，超调量小，鲁棒性好等优点，特别适合于非线性和时变的控制对象。不足之处在于模糊控制的静态误差较大。结合PID控制和模糊控制两者的优点而对复杂对象进行有效控制成为当前的研究热点。并且在温度、倒立摆系统、电动舵机驱动系统得了阶段性研究成果[3]。

1 模糊PID控制

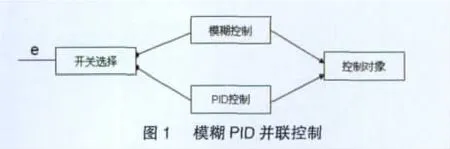
模糊控制和PID控制的结合控制方法，目前主要集中在两个方向：一种是模糊PID并联控制，如图1所示，对误差进行实时跟踪，误差大时用模糊控制，以加快系统的反应速度，减小超调量；误差小时用PID控制以控制系统的静态误差。这种控制方式的困难之处在于控制量易于在控制阈值附近形成震荡，达不到控制要求，有研究表明使用模糊阈值，并且通过遗传算法对复合控制器的量化因子和积分系数进行在线优化，可以改善这种情况[4]。

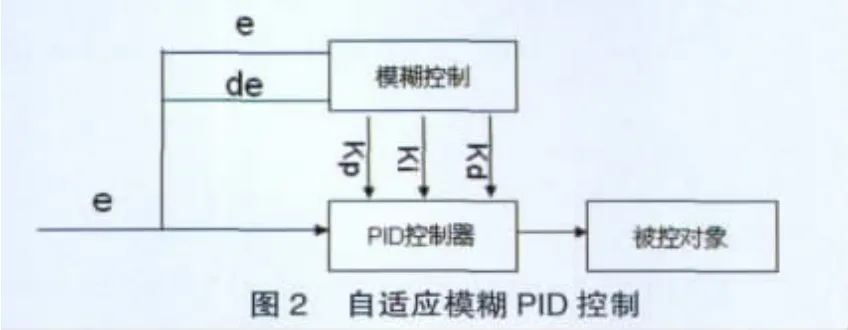
另一种结合方式是模糊自适应PID控制，如图2所示。这种方式也对系统误差实时监控，根据误差和误差的变化率在线动态调节PID控制算法中比例、微分和积分的控制参数，达到即减少系统超调、缩短稳定时间，同时又不引进大的稳态误差。本文所设计的模糊自适应PID控制算法基于这种模型。

2 模糊自适应PID算法的控制思想和设计总原则

2.1 模糊自适应PID算法的控制思想

系统设计时，根据Ziegler-Nichols整定方法，采用PID控制方法对系统进行预控制，达到系统的稳态要求，记下所整定的比例Kp、积分Ki和微分Kd参数。然后设计模糊控制，根据输入变量的隶属度函数和模糊规则表，运用模糊推理的方法得出各参数的动态值，用模糊控制的输出在线调整PID参数。

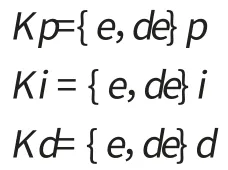
2.2 模糊自适应PID参数设计总原则[5]

（1）当误差较大时，为加快系统的响应速度，应该取较大的Kp，这样系统的时间常数和阻尼系数减小。当然也不能过大而引起系统的不稳定。为避免系统在开始时可能引起的超范围控制作用，取较小Kd，以便加快系统响应；同时为避免出现大的超调，可以尽可能的减小Ki；（2）当误差处于中等大小时，应取较小的Kp，是系统响应的超调略小，此时的Kd的取值对系统较为关键，应取合适的值；此时可以增加一点Ki，但不要过大；（3）当误差较小时，应取较大的Kp和Ki，为避免系统在平衡点出现震荡，Kd的取值应适当。

3 模糊自适应PID算法的设计

3.1 输入和输出的模糊化

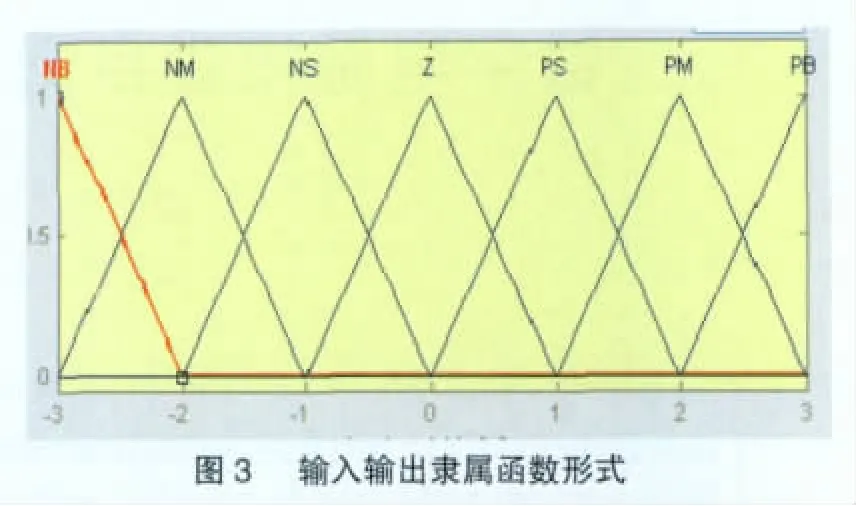
模糊自适应PID的输入为误差E和误差变化率DE，输出为Kp，Ki和Kd。在本例中，各变量的模糊子集均为{NB,NM,NS,Z,PS,PM,PB}，其表示的含义为负大，负中，负小，零，正小，正中、正大。误差E的论域为[-3 3]，误差变化率DE的论域为[-1 1]，输出Kp的论域为[0.4 1.6]，Ki论域为[0 400]，Kd的论域为[0 1]，隶属函数采用三角函数，在论域上全交叉均匀分布[6]。其形式如图3所示。

3.2 模糊规则表

模糊规则表式根据PID三个参数Kp，Ki和Kd对系统的控制效果，结合理论以及实践中的控制经验而制成，采用模糊条件推理if A and B then C形式，称为IF-THEN规则。该控制表是模糊控制器模糊判决的依据，模糊控制的优势就体现在不仅能对系统输入输出隶属函数进行调节，还可以根据具体的控制系统对模糊规则表进行微调。本例中采用的模糊规则如表1所示。

?

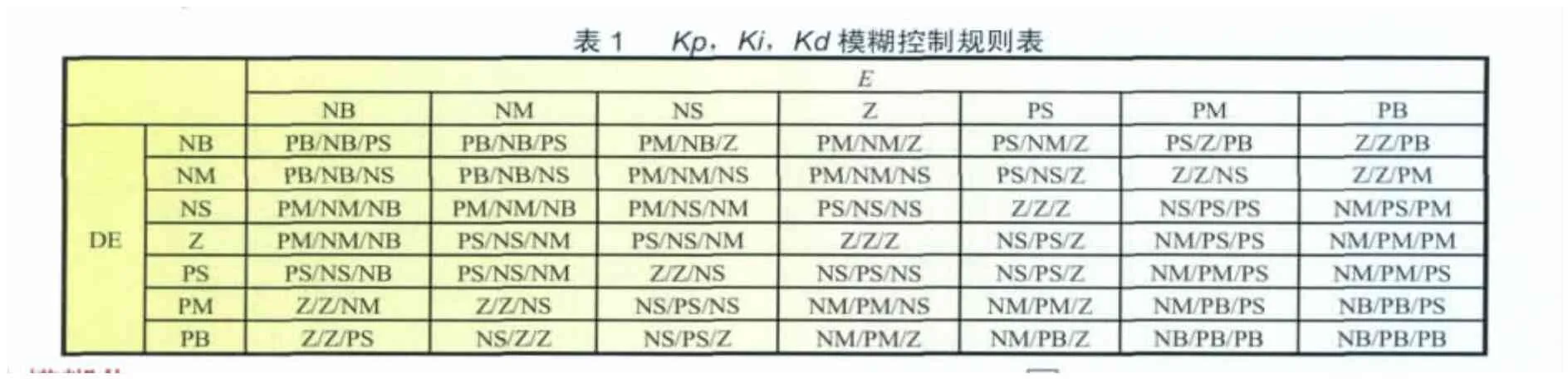
3.3 去模糊化

依据模糊规则和模糊推理所得到的输出是一个模糊量，而数字电源的控制必须是一个精确量，这就需要把模糊自适应PID的输出经过去模糊化。常用的去模糊化方法有最大隶属度法、面积中心（重心）法和面积平分法。本例中采用的是面积平分法。其计算形式如下[7]。

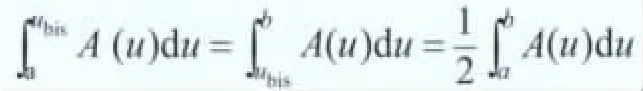
式中:ubis为输出精确值，A(u)为隶属函数，(a，b)为隶属函数的论域。

4 系统仿真研究

4.1 系统构建

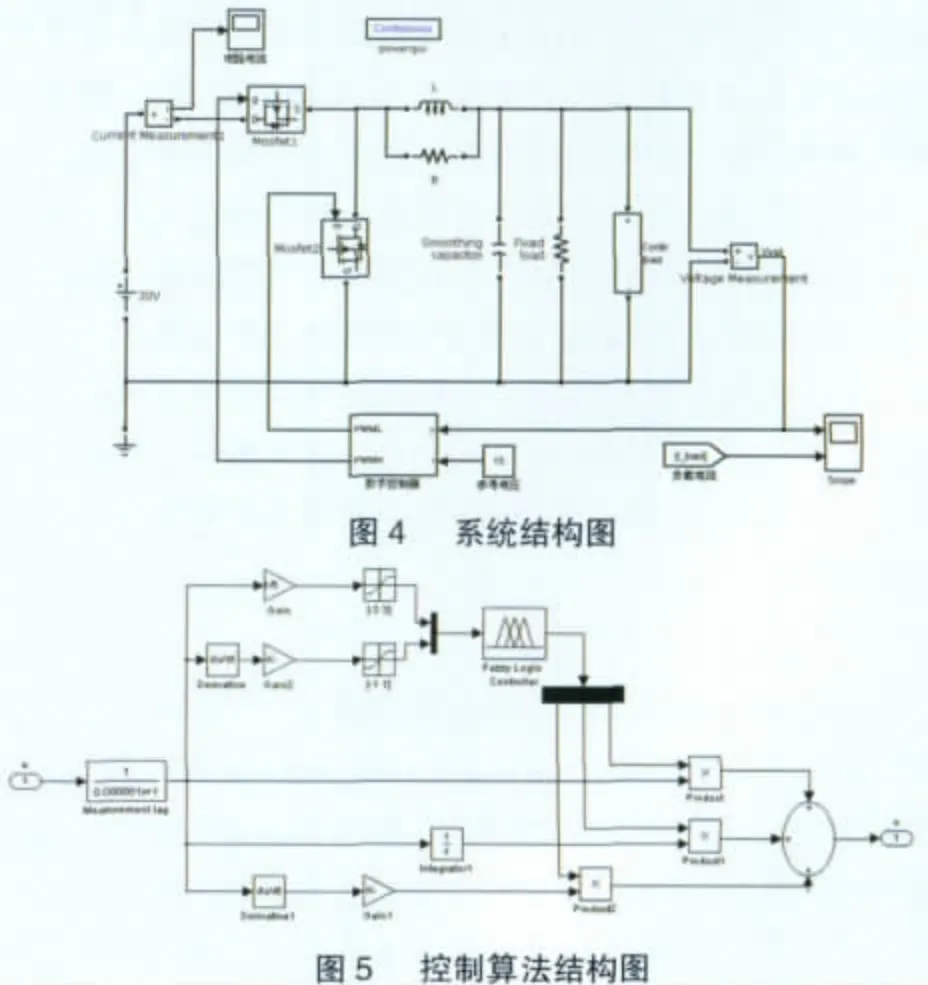
本文基于MATLAB/SIMULINK对自适应模糊PID算法进行了仿真研究。研究系统如图4所示，系统采用经典的DC/DC同步整流BUCK电路。输入直流电压为30 V，输出参考电压为15 V，图中电感取值为1 mH，滤波电容为22μF负载电阻为3.75Ω，工作频率为50 kHz。负载电流通过Cyclic load改变，其周期设为1/200，幅值为2 A。

数字控制器的设计：数字控制器是该系统的核心组成部分，控制算法结构如图5所示，为了和实际情况更加接近，算法前面引入1μs的延迟环节代表测量延迟，误差量化因子取为0.2，误差变化率量化因子取为10－5，模糊控制模块中的函数为上文所设计的模糊控制函数。控制器的通过调节输出值u，调节PWM Generator模块产生PWM波的占空比D来控制系统。

4.2 仿真结果

为了说明模糊自适应PID控制的控制效果，本文对比了常规PID算法和模糊自适应PID算法。仿真结果如图6所示，从图6中可以看出模糊自适应PID控制比数字PID控制算法稳定速度快，超调量小。

[1]郇惠云.数字电源概述[J].中国西部科技，2009，8（16）：31-32.

[2]WANG G C，ZHANG M，XU X H，et al.Optimization of controller parameters based on the improved genetic algorithms[C]//Proceedings of the 6th world congress on Control and Automation(WCICA 2006).Dalian：WCICA 2006，2006：3695-3698．

[3]李保强，任天平，刘玲玲.模糊自适应PID在叶腊石烤箱温度控制中的应用[J].机械设计与制造，2010，12（12）：77-78.

[4]孟珺遐，王渝，王向周.Bang-Bang+Fuzzy-PI自适应控制器的应用研究[J].机床与液压，2008，36（10）:266-270.

[5]王贵成，汪勇，张占胜.自适应模糊PID控制器的设计[J].仪器仪表学报，2008，29（4）:553-555.

[6]黄卫华，方康玲，章政.典型模糊控制器的隶属函数设计及分析[J].模糊系统与数学，2010，24（5）:83-89.

[7]石辛民，郝整清.模糊控制及其MATLAB仿真[M].北京:清华大学出版社，2008.