蓄电池可接受充电电流预测

王 丽，高 田，景志林

（1.塔里木大学机电学院，新疆 阿拉尔 843300；2.西北工业大学电子信息学院，陕西 西安，710072；3.新疆电力科学研究院，新疆 乌鲁木齐 830011）

蓄电池作为电力供应设备在国防通信、交通运输和医疗卫生等诸多领域都有应用。电池的使用寿命由对其进行能量补充的充电装置决定的，而简单的充电装置智能化程度不高，缺乏自适应能力，不能跟踪电池充电特性的改变而动态调节充电电流或及时地停充电。因此，众多学者针对蓄电池的安全、高效充电技术进行了许多深入的研究，提出了各种不同的快速充电技术，如脉冲充电方法、大电流恒流充电法、多阶段恒流充电法、大电流限流恒压充电法以及负脉冲充电法等[1-2]。但是，所有这些充电方法都不能使电池按其自身的可接受电流充电曲线进行充电，导致析气多，温升大，对电池损害严重的问题。

近年来，先进的智能控制技术引入到电池的充电过程，提高了充电速率和控制精度，取得了一定的成果[3-4]。但没有从电池特性出发考虑电池的可接受电流这一根本问题，早在1980年，原苏联的雷兹洛夫就指出：铅酸蓄电池在放电态有短时接受很大充电电流的能力；蓄电池可接受的充电电流随充电时间指数下降，按此规律进行充电，充电时间最短，效率最高[2]。李蓓也提出当初始充电电流与初始电解液密度之间保持“最佳配比关系”时，可获得最大电流衰减指数，即达到单体电池最大充电接受率[5]。本文在此基础上，对镉镍电池和氢镍电池进行研究，提出根据电池本身的充电特性，引入自适应神经网络推理系统（ANFIS）对电池的可接受充电电流进行预测，以此调整实际充电电流，指导充电进行。

1 蓄电池的可接受电流分析

1.1 蓄电池的等效电路

文献[6-8]中提到蓄电池可以简单地看作一个超大阻容器，对电池的快速充电过程实质上就是RC 电路的充放电过程。将可充电设备的电池看作是充电装置的一个电容性负载，其充电过程可用如图1所示的等效电路表示。

1.2 可接受电流分析

上世纪60年代中期，美国科学家J.A.Mas 在大量实验的基础上，提出了以最低析气率为前提的蓄电池可接受充电电流曲线(简称马斯曲线)，如图2所示，这已成为快速充电技术的理论基础。

图1 电池充电等效电路

图2 蓄电池可接受的充电电流曲线

马斯曲线描述了电池容量、电池的充放电历史以及电池最大可接受充电电流之间的数量关系。马斯曲线可描述为：

式中：Ic为蓄电池可接受的充电电流；I0为t=0 时刻可接受的最大充电电流；α为充电电流的充电接受比，又称固有接受比，α=I0/C(C为电池的额定容量)；t为充电时间。

马斯的最低析气率充电电流曲线按指数规律衰减，主要原因是：（1）参与反应的活性物质减少，（2）极化现象对充电产生了阻碍。在快速充电过程中，如果使实际的充电电流接近或等于蓄电池可接受的最大充电电流，则充电速率提高，且析气率可控制在很低的范围内。而实际的充电过程中，电池的可接受充电电流曲线很难找到，由于电池的个体差异和使用中电池本身所发生的变化，以及电池荷电状态的不同等都会影响电池的可接受电流。

但是，我们在实验中发现：因为α=I0/C，对同类电池在深放电状态电流的可接受比α是一定的，根据蓄电池的等效电路可将α等效为RC 电路的时间常数1/τ，则式中Req、Ceq分别为电池的等效电阻和等效电容。电池充电是进行电荷能量的补充，下面分别计算t=3τ和t=5τ时电池所充入的电量，分别记为Q3τ和Q5τ：

由式(2)和式(3)可知，t=3τ时，电池所充电容量为85%C；t=5τ时，电池所充电容量为99.3%C，即t=5τ时，电池基本充满电。而相应的可接受电流为：

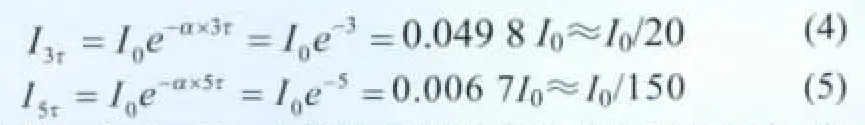
由公式(4)和(5)可知，在按马斯曲线进行充电的过程中，电池的可接受电流的大小只与初始电流I0有关，且对于荷电状态相等的同类电池经过相同的时间后，其可接受的最大充电电流也基本相同。当经过时间3τ后，可接受的充电电流很小(约为I0/20)；当充电到t=5τ时，其电池的可接受电流大小约等于电池的自放电电流。则镉镍电池和氢镍电池的充电过程中，电池电压和可接受电流对应关系如图3所示。

图3 电池电压和可接受电流对应关系

由此可知，同类电池在深放电状态下充电电流曲线相同，初始可接受充电电流I0差别也不大，曲线总体按指数规律变化趋势基本相同。当某容量电池在深放电时的初始可接受电流确定后，电池的可接受电流曲线就可以确定。

1.3 初始可接受电流I0

2 应用ANFIS预测蓄电池可接受电流

2.1 ANFIS

基于自适应神经网络的模糊推理系统ANFIS 是用神经网络结构来表示模糊推理，同时具有模糊逻辑易于表达人类知识和神经网络的分布式信息存储以及学习能力的优点，对于复杂系统的建模和控制提供了有效的工具。ANFIS 建模的主导思想是建立一个能容纳模糊信息的神经网络，神经网络通过对样本数据的学习，能够有效地计算出隶属度函数的最佳参数，使得设计出来的模糊推理系统能够很好地模拟出希望的或是实际的输入输出关系。

2.2 ANFIS预测可接受电流基本思想

本文根据马斯的快速充电理论，深入分析镉镍电池可接受电流的变化规律，提出利用ANFIS 预测电池的可接受电流。

ANFIS 预测电池的可接受电流基本思想是：在充电过程中，动态检测电池的状态参数作为ANFIS 预测模型的输入，通过模糊推理得出当前的可接受电流ick，当预测值ick与期望值icp的误差不满足要求时，自适应模糊控制器产生控制响应，通过神经网络的自学习能力，自适应地修正隐含层的输出结果，更新各层之间的连接权值，优化模糊参数，重新计算输出结果，直至误差满足要求才输出预测结果，从而改变当前的充电电流，使实际的充电电流始终逼近或等于可接受电流。原理框图如图4所示。

图4 应用ANFIS 预测可接受电流原理框图

2.3 ANFIS模型的建立

由于ANFIS 是一种基于数据的建模方法，模型通过对样本数据的学习，调整和优化模糊系统的参数；同时，一个训练好的模糊神经网络模型应该具有很好的泛化能力，即当除样本数据以外的其它数据出现时，网络也能产生准确的输出。由于不同电池的可接受电流不相同，故本文主要针对同容量同类电池建立ANFIS 预测电流模型，当然ANFIS 预测电流方法也适用于其它镉镍/氢镍电池。在实际充电时，电流不能太高，因此，这里只对图3中A-C 段采用ANFIS 进行预测电池的可接受充电电流。

预测模型的建立过程如下：

（1）输入变量的选取：表征电池充电状态的变量很多，根据前述分析，这里选取电压差值和电流大小表征电池的充电状态。两个输入变量分别为：(1) 选取A-C 段的最高理想电压Vmax和实际测量电压Vi之差值 ΔV(ΔV=Vmax－Vi)；(2)选取某个时刻电池的充电电流ic(t)。输出变量是下一时刻电池可接受的充电电流ic(t+1)，本文用ick表示。则该模型可以用如下方程来表示：

（2）模糊神经网络结构：由于ANFIS 模型通过训练只能调整参数，不能改变模糊规则数，而且对于电流预测不是十分复杂，完全可根据电池电压和当前的充电电流大小决定电池的充电状态，因此，我们设计的模糊神经网络结构预先设定好，即这里只研究静态的模糊神经网络，不对其结构再进行辨识。

对每个输入变量的输入空间划分为3 个模糊集，分别用大(B)、中(M)、小(S)三个语言变量表示，从而得到9 条模糊规则，对应输出的9 个模糊区域。

（3）ANFIS 模型的初始化：ANFIS 模型初始化任务主要是初步确定隶属度函数类型及其参数。在镉镍电池的快速充电实验中，获取电压和电流信息通过滤波之后作为ANFIS 模型的输入，在两输入变量的九个模糊空间中，通过插值均匀地获取对样本数据集，数据集均匀分成训练集和测试集，训练集用于模型的学习训练，根据输入数据和期望输出的关系，调整神经元间的连接权值，进而改变输出。测试数据用于测试网络的泛化能力，即网络不仅仅记住样本数据，当有新的数据出现时，网络也能产生准确的输出[9]。

（4）ANFIS 预测模型的训练和学习：

12 V/4.5 Ah 镉镍电池的额定电压为12.5 V，这里，先对4.5 Ah 镉镍电池放电到端电压为1.0 V/节左右，使电池在深放电状态下进行快速充电实验，在充电过程中，电压缓慢上升，充电终止电压可达到17.6 V，电池温度从室温23 ℃上升到38 ℃，则电压差值ΔV的变化范围为[0，5 V]。考虑到单片机的检测精度和控制的可靠性，系统检测间隔Δt取120 s。电池的可接受充电电流ic根据电池特性和马斯定律等相关理论确定初始值。电池在深放电状态下的最大可接受电流I0，与电池容量和电池内部参数等有关。一般来说，电池容量越大其可接受比α越小，如1.8 Ah 的镉镍电池最大可接受电流为2.5C，而4.5 Ah 的镉镍电池的最大可接受电流为2C。则4.5 Ah 的镉镍电池在A-C 段的可接受电流的变化范围为[0.4 A，9 A]。这样获取75 个数据对，用于训练ANFIS 模型。首先对训练数据集进行归一化处理，然后在ANFIS 中导入样本数据进行模型的训练，采用优化算法来训练网络，调整模型的参数。给定输入数据和RBF 节点函数，计算出第j个RBF 单元的输出Rj(称为前向通道)，采用线性最小二乘法使均方误差最小修正权值；然后，继续向前直到计算出输出误差；然后，误差反传，即输出误差从输出端传到输入端，称为后向通道，采用梯度下降法更新前件参数，从而改变隶属函数的形状。

3 测试结果分析

对4.5 Ah 镉镍电池先放电到端电压为1.0 V/节左右，再进行快速充电。这里4.5 Ah 镉镍电池在深放电状态下的初始可接受电流为I0为2C。通过参考模型获取电压差值ΔV和每隔2 min 测出当前充电电流的数据信息，输入到训练好的ANFIS 模型中，预测出电池下一时刻可接受电流值，实际的和期望的电池可接受电流变化曲线如图5所示, 误差曲线如图6所示。

图5 实际的和期望的可接受电流变化

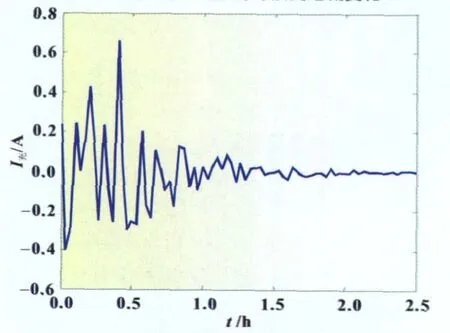
图6 误差曲线

预测结果表明，该模型对快速充电中后期的预测效果明显比充电的起止端的效果好，总体预测的误差不超过8%，能满足实用要求。

4 结论

本文引入ANFIS 预测充电过程中电池的可接受电流，进而调整实际的充电电流，保证电池充电电流始终处于电池的可接受电流值附近，保证最优快速充电，析气率低，有效地消除了极化效应，充电效率高，减少了后期电流过高对电池造成的损害。

文中的ANFIS 模型选取便于精确测量的电压信息作为输入变量，训练样本是对同一种类的电池从深放电状态开始充电实验而获得，但是由于网络具有较好的泛化能力，一旦模型训练好，则可对任意荷电状态的电池预测出可接受电流。若要对其它类型的镉镍/氢镍电池应用本模型进行预测电流，只需在应用前采集相关的数据，对模型进行离线训练，然后用于在线实时预测。在实际使用中，由于电池具有离散性和复杂性等特点，最好能对ANFIS 模型进行结构辨识，选取最有效的输入变量，提高预测模型的精度。

[1]周志敏，周纪海，纪爱华编.充电器电路设计与应用[M]．北京：人民邮电出版社，2005.

[2]郭自强.关于快速充电（之一）[J].中国自行车，2010，9：40-44.

[3]FARAG W A，QUINTANA V H，TORRES G L．A genetic-based neuro-fuzzy approach for modeling and control of dynamical systems[J]．IEEE Trans.Neural Networks，1998，9(5)：56-767.

[4]CAI C H，DONG D，GE J T，et al.Batteru-charging model to study transient dynamaics of battery at high frequency[J].Proceedings of IEEE Tencon，2002(2)：1843-1846.

[5]李蓓.蓄电池初始充电电流和充电接受率的研究[J].蓄电池，2008(4)：171-174.

[6]GONZALEZ M，FERRO F J，ANTON J C．Considerations to improve the practical design of universal and full-effective NiCd/NiMH battery fast-chargers[J]．IEEE，1999，10(19)：167-173.

[7]HUA C C，LIN M Y．A study of charging control of lead-acid battery for electric vehicles[J]．International Symposium on Industrial Electronics，ISIE，2000，9(5)：135-140.

[8]LIMA F，RAMALHO J N，TAVARES D．A novel universal battery charger for NiCd，NiMH，Li-ion and Li-Polymer[J]．IEEE，2003，44(1)：209-212.

[9]王丽，景志林，景占荣.基于ANFIS 的氢镍电池快速充电过程优化[J].现代电子技术，2007（24）：197-199.