莱钢宽厚板轧机系统厚度自学习模型的研究
2012-07-05孟帅刘疆李克
孟帅 刘疆 李克
(山东省莱芜市莱钢集团自动化部)
0 引言
在宽厚板轧机系统中,影响厚度的因素有很多,因此厚度的精确计算十分复杂。在建立厚度计算模型时,厚度自学习修正值是最重要的参数。只有准确的修正值,才能得到精确的厚度,以达到最佳的轧制效果。厚度自学习算法有多种(例如:复杂非线性优化算法和有线性约束的规则库推理方法等),涉及数据量也很大,因此对厚度自学习模型的深入探索有助于轧机厚度模型的研究。
1 厚度计算
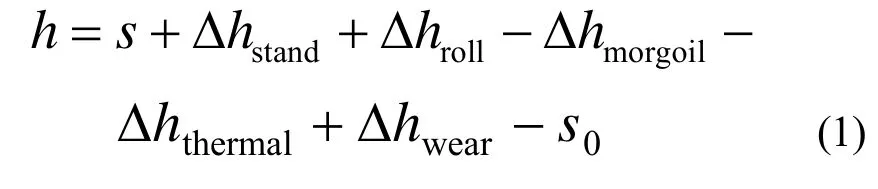
随着现代工业轧制技术的发展,对宽厚板的厚度精度提出了更高的要求。只有尽量把影响厚度的因素都考虑在内,才能得到精确的厚度值。根据可用的测量值,通过厚度计算公式可得到钢板轧制后的厚度:式中:h为厚板的出口厚度;s为辊缝;Δhstand为机架拉伸带来的厚度偏差;Δhroll为轧辊变形带来的厚度偏差; ΔhMorgoil为轴承油膜厚度带来的厚度偏差;Δhthermal为轧辊热凸度带来的厚度偏差;Δhwear为轧辊磨损带来的厚度偏差; s0为零点[1]。
由式(1)可以看出自学习的核心就是对零点 s0的自学习,因此研究零点自学习的计算是关键。
1.1 机架拉伸
机架的变形(不包括轧辊)也称为机架拉伸。机架拉伸的原因有:轧制力、弯辊力、工作辊弹性变形恢复力。
变形阻力是在咬钢时产生的。这时,轧制力测量值一部分是由轧件的变形阻力构成,另一部分是由工作辊恢复原形的力构成,也就是所谓的恢复力。恢复力仅仅在辊缝很小的时候产生。
1.2 轧辊变形
整个辊系(包括工作辊、支撑辊、厚板)的变形称为轧辊变形,包括以下弹性变形:
1)工作辊和支撑辊的偏转;
2)工作辊和支撑辊之间的变形恢复;
3)工作辊和厚板之间的变形恢复。
轧辊变形的因素包括:轧制力、弯辊力、辊形(由摩擦、热凸度和磨损引起的辊形改变,由CVC引起的辊缝改变)[2]。
1.3 轧辊热凸度和磨损状态
辊形不断地变化是因为轧辊在轧钢和空闲时,交替地受热和冷却,辊形也因为磨损而变化。热胀冷缩导致的辊形变化被称为“热凸度”。磨损导致的辊形变化被称为“磨损凸度”。
热凸度和磨损凸度受很多条件的影响,如冷却模式、钢板温度、钢板变形等。此外,历史轧制数据也是影响因素之一。热凸度和磨损凸度通过TWM模型(热凸度和磨损模型)来计算。
1.4 油膜
轴承油膜厚度的变化主要受两个值的影响:轧制速度和轧制力。
当轧制力增大时,油膜厚度减小;当轧制速度增大时,油膜厚度减小。
在对上述各个因素不断完善后,厚度命中率见效甚微,因此对变数最大的 s0零点进行了重点攻关。
2 宽厚板的自学习模型
2.1 短期自学习
每完成一个道次轧制后,计算与该道次机架相关的所有设定值。根据实测轧制力、实测辊缝、实测弯辊力等条件计算出钢板的实际出口尺寸。把这些值与实测值进行比较,得到的修正因子,称为短期自学习因子。短期自学习因子只对本块钢板的下一道次进行修正。
2.2 长期自学习
最后一个道次轧制完成后测厚仪测得钢板厚度实测值后,辊缝零点会用测厚仪的实测厚度减去程序模型计算出的厚度得到一个偏差值,对该偏差进行处理后得到自学习修正因子,称为长期自学习因子。长期自学习因子将对下一块钢板进行修正(开始轧制前)。
3 辊缝零点及其自学习
3.1 标定零点
这里的“零点”是由标定过程决定的。在标定中,将上下轧辊以某个速度压靠在一起,直到达到一个特定的压力。
这样式(1)的厚度值可以设为0,零点厚度与厚度计算公式中所有项之间的差可以用式(2)计算。
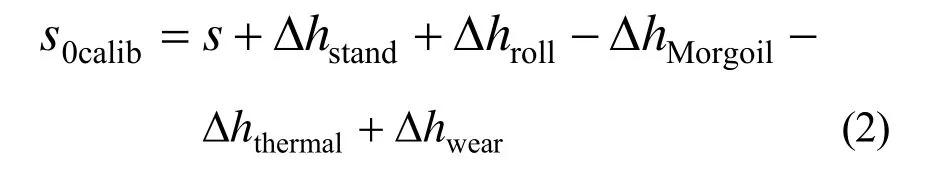
这个差值就是“零点”。更精确的讲,它是标定的零点[3]。在轧制过程中,零点可以通过厚度测量进行自学习调整。
3.2 零点自学习调整
自学习过程是一个不断逼近目标的过程,其核心思想用数学模型来表述,称为自学习算法。通常采用基于梯度的算法,其中最小均方误差算法(即 LMS算法)最为常用[4],其优点是可完成的运算复杂度较高,更适合数据量庞大的运算。宽厚板轧机系统自学习模型采用的就是该算法。
当进行厚度测量时,零点会自动调整。为了得到厚度计算公式中的各项,需要确定轧制力、轧制速度等,以及轧辊的热膨胀、磨损状态。所以,零点可以用式(3)修正。
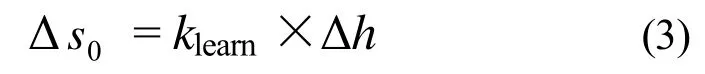
自学习因子klearn的范围在 0~1之间,以保持稳定,通常为经验值;Δh为厚度偏差。
3.3 厚度偏差的计算
3.3.1 厚度偏差计算公式
通过比较厚度测量值和厚度计算公式算出的厚度,可以确定厚度的误差。
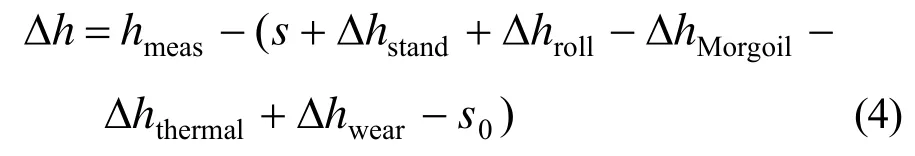
3.3.2 测厚厚度值hmeas的噪声过滤
每块钢板通过测厚仪后,都会收集到许多厚度测量值,密集地分布在钢板的多个位置,它们的值会有波动较大的偏差(如图1所示),因此如果要使用该测量值,必须对所有的厚度值进行过滤。过滤采用标准偏差的计算方法,用于剔除样本中的噪声点。
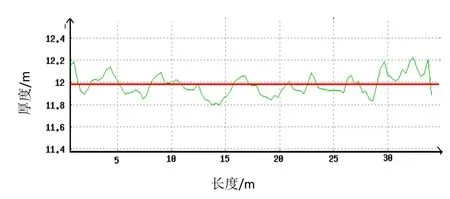
图1 长度方向上测量的厚度曲线
标准偏差(也称标准离差或均方根差)是反映一组测量数据离散程度的统计指标,是一种量度数据分散程度的标准,用以衡量数据值偏离算术平均值的程度,是反映一组测量数据离散程度的统计指标,可用来统计结果在某一个时段内误差上下波动的幅度。标准偏差越小,这些值偏离平均值就越少,反之亦然。

式中:S为标准偏差;n为样本总数或测量次数班,一般n值不应少于20~30个;xi为样本值;i为标识第i个样本,取值1~n。用过滤后的测量值减去厚度模型的计算值,得到厚度偏差,最终计算出可以修正厚度的零点,得到一个更加精确的厚度计算值。
4 结语
通过对厚度自学习模型的研究,不断修正测量厚度偏差,不断逼近精确计算值,更好地提高厚度计算的精度。就莱钢宽厚板项目而言,投入厚度自学习模型后,厚度控制命中率由投入前的91.75% 达到了投入后的95.35%(见表1)。目前,莱钢宽厚板厚度自学习模型在生产中的厚度控制命中率为96%,对轧钢厚度命中和提升产品质量起到了至关重要的作用。
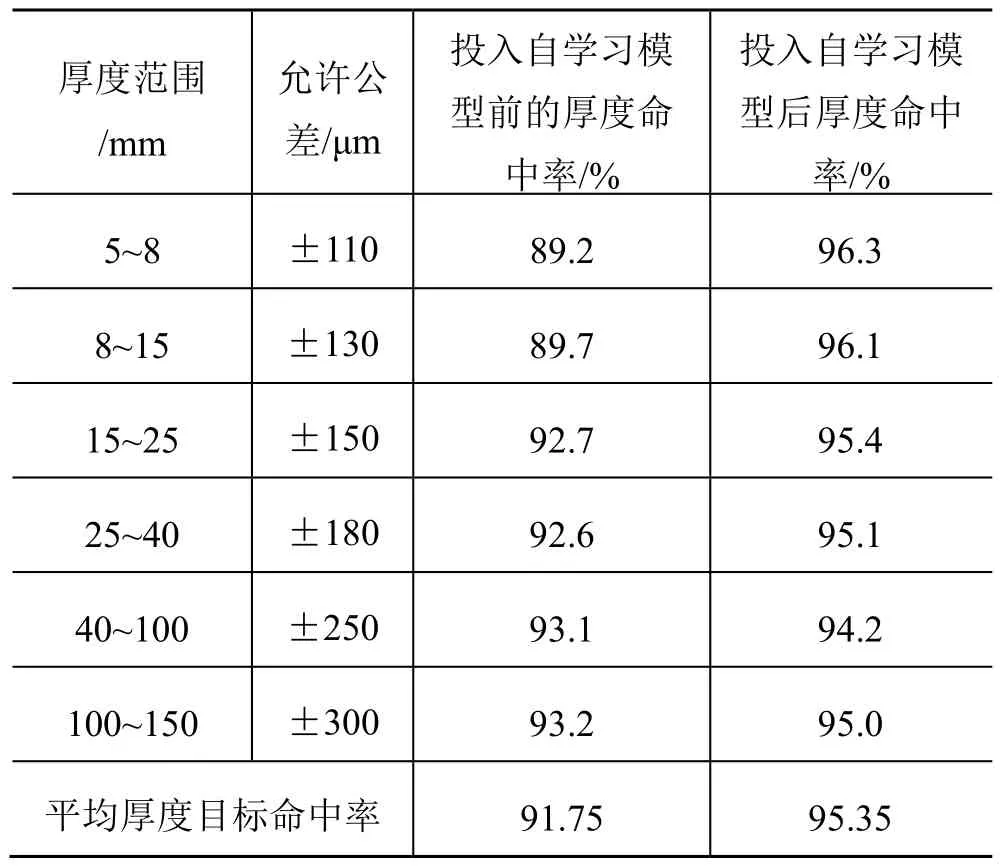
表1 投入自学习模型前、后的命中率统计
[1]邱红雷,胡贤磊,赵忠,等.中厚板轧制过程中的辊缝设定模型及其应用[J].钢铁,2004,39(12):36-39.
[2]胡贤磊,王昭东,刘相华,等.轧辊弹性变形对中厚板辊缝设定的影响[J].东北大学学报:自然科学版,2003,24(3):284-287.
[3]张少锋.4100mm厚板轧机厚度自适应模型的研究与应用[J].宽厚板,2008,14(6):22-25.
[4]高利娟,刘云.基于联合检测在时分同步码分多址技术中的多径干扰分析下载[J].成都信息工程学院学报,2010,25(5):472-475.
