大整数基本运算的实现分析

2012-07-05柴君

科技传播 2012年9期

柴君

天津电子信息职业技术学院，天津 300350

0 引言

首先，我们来阅读如下简单C语言程序:

很显然，如果是在Turbo C环境下运行，则输出的结果是字符串no。出现这种结果的原因也不是很难分析:由于计算机给任何数据分配的内存空间都是有限的，它不能直接存放任意大或者任意精度的数据。但是在计算机应用中，尤其是信息安全密码学和科学计算中，大数运算和高精度运算有着普遍的需求。在这种矛盾中，对超过范围的数据（这里的范围包括大小和精度:普遍的开发环境中，long型的数据大小小于1011，double型的数据精度小于16位），就必须设计新的数据结构进行存储，并定义基于新结构的基本运算[1]。在本文中，我们将分析大整数的存储和运算的实现。

根据如何存储大整数的方法不同，我们将实现方法分为数组方式实现和链表方式实现两种。

1 数组方式实现分析

1）大整数数组存储

在数制表达当中，进制数（即基数）是基础。一个整数A表达成 A = (a0a1… an)，其实际表示的是一个以 a0、 …an为系数的多项式: A =，其中的X表示基数[2]。所以，存储一个大整数，实际上就是存储这些系数，而最直观的就是数组存储了。但如果一个数组元素存储一个十进制系数，会存在明显的空间浪费，运算实现过程也会出现循环次数过多的问题，效率低。因此要选择合适的基数X:分析发现如果取X=10000是比较合适的，一方面并没有超出long型数据的范围，另一方面会减少大整数的实际位数，提高空间和时间上的效率。同时，十进制数转换为万进制数不会改变大整数原有的数字形式，也就不需要多余的数字转换运算，只需要把原数的每四位看成一个整体，依次存入数组而已。需要注意的是，原整数低位在右侧，而数组的低位在左侧，因此为了计算方便，存储时，新的万进制数采取逆序存放。按照如上描述，一个大整数98765432109876543210采取上述方法存储如下样子（每一段对应一个数组元素，并与数组元素先后次序一致，第一个数即为下标0的元素，注意最后一个的位数可能小于4）:

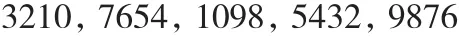
而为了运算和判断的方便，我们还须对大整数进行结构封装，增加记录“系数个数”和“正负符号”两个成员。因此可得大整数结构如下:

2）大整数加减法

对同正或同负的两个大整数，它们之间的加法运算，和的符号同加数，和值只需对两个加数数组的对应元素相加，并考虑进位即可。两个加数A和B的系数个数（也就是数组有效元素个数、或整数的位数）的大小关系存在三种可能，因此在实现中，以较少的系数有多少个来划分有较多系数的加数，这样就可以对低位相同长度的部分对应相加，对高位多出的部分直接赋值到和数组。

对异号整数的加法运算，实际上是减法运算。它的运算过程与同符号加法相类似，也需要对系数较多的加数进行划分，低位相同长度的部分相减，高位部分直接赋值。不过在运算之前需要作预处理:首先要比较两个数的大小（不考虑正负号），把较大的数作被减数，经过这步处理，也可以确定差值得符号——与较大的数相同，然后作减法运算。

3）大整数乘法

首先，我们分析一下自然乘法运算的过程:排竖式依次用乘数的每一位去乘被乘数的各位数字，再加上上一步运算的进位，最后累加结果。

以上过程是非常有规律的，两个运算数A和B也都是逆序存放在数组中，因此可以利用for语句逐步进行:首先定义积数组result并初始化为0，则自然乘法运算的过程可以对两个运算数数组下标进行循环，同时依次相乘和最后累加这两个步骤可以进行合并:

result[i+j] += A[i] * B[j] % 10000; //各位数字乘积对基数的模存放在第i+j位

result[i+j+1] += A[i] * B[j] / 10000; //乘积对基数的商表示需进位，并进位到高一位

以上所述实现的是乘法的自然算法，不难发现该算法需频繁地进行模、商和进位运算，增加了运算次数，对这一点我们还可以进行如下改进。

自然算法过程是依次出现每行的乘积，然后对应列相加，从而导致模、商和进位运算重复进行。我们改变运算次序，先计算每一列的数字(各位数字相乘但不进位)，然后再进行横向的运算:在最后才开始从低位向高位逐位进行进位修正。方法是:模留在本位，而商则进位到高一位。

4）大整数除法

除法运算是最复杂的，也是效率最低的。根据除法的一般定义，我们可以借助减法来实现:以差值是否小于除数作为判断条件进行循环运算，以一个计数器统计循环次数，则计数器的终值即为商，最终的差值即为余数。

2 链表方式实现分析

1）大整数链式存储

同前面一样，取基数X=10000，将大整数从低位每4位构成一个系数存入链表的每一个结点。同样考虑到输入输出数据时高位在先，而计算时一般从低位开始，因此采用双向链表存储大整数。这样一个大整数就对应了一个链表，并给该链表设置一个头结点，该结点的数据域表示大整数的符号及系数个数:数据域的符号与大整数符号一致，绝对值则表示系数的多少。因此可得大整数的结点结构如下:

2）链表存储的基本运算算法和前述的方法差别不大，将遍历数组换成遍历链表即可。

3 输入输出处理

大整数的输入可以从键盘输入，也可以从文件读入。如果从键盘输入，则按照字符输入，首先读取首字符正负号，一般正号不输入，首字符如果是负号，则修改数据结构中相应的字段:数组方式中的sign成员或链表方式中的头结点。后续的数字连续输入构成一个字符串，将该字符串从后往前遍历，每四位一组存入数组元素或结点数据域。

如果从文件读取大整数，处理相对简单，可以使用相关库函数分段截取，存入数组元素或结点数据域[3]。

对数据的输出，由于选用的基数的关系，各数字形式未发生变化，因此只需逆序遍历数组或链表，依次输出数组元素或链表的数据域。