基于变周期重播种LFSR的测试生成
2012-07-04包清明潘红兵
包清明, 潘红兵
(海军工程大学电子工程学院,武汉 430033)
0 引言
在现代测试中,内建自测试(Built-in Self Test,BIST)[1-2]技术是满足系统可测试性和故障诊断要求的重要手段。BIST的主要部分包括测试序列生成器,测试响应分析器和测试控制器等。其中测试序列生成器主要有确定性测试序列生成器,伪随机测试序列生成器以及混合测试序列生成器。确定性测试生成主要是通过确定性算法,如 D 算法[3]、PODEM 算法[4]等,计算出电路的全部故障测试序列,然后将其存储到BIST的ROM中。它能产生最小测试序列集,施加测试时间较短,故障覆盖率高,测试效率较高。但其序列的计算过程复杂,在电路规模较大时,用于存储测试序列的硬件开销较大。
伪随机测试序列生成器通常采用线性反馈移位寄存器(Linear Feedback Shift Register,LFSR)来实现[5],其所需成本小,硬件实现简单可靠。但是伪随机测试生成方法的故障覆盖率难以提高,且不能解决难测故障的问题。为了克服线性反馈移位寄存器作为伪随机码生成器的缺点,提出了重播种LFSR和ROM混合测试生成结构[6-7],用 LFSR 产生加权随机测试码[8]等混合测试序列生成方案。然而加权测试生成法需要存储数量较大的测试加权集,硬件开销大,重播种方案中种子产生的伪随机测试序列是等长的,其冗余随机测试序列仍较多。
针对此问题,本文提出一种变周期重复播种测试生成法。该方法可以有效地跳过测试生成序列中的冗余序列,缩短总的测试序列长度,在保证故障覆盖率的条件下,减少测试施加的时间,从而提高测试效率。
1 LFSR结构周期重播种测试生成
由于所需成本小,硬件实现简单可靠,基于LFSR结构的测试向量生成器已经成为BIST的主要结构。其方法对于组合电路和时序电路测试都适用。常用具有最大周期的LFSR产生的m序列作为伪随机测试激励,此时该LFSR的特征多项式为一本原多项式,在伽罗华域GF(2)上该多项式表示为
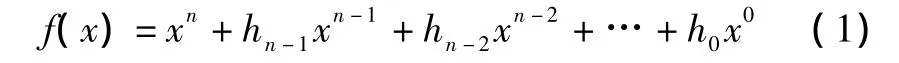
测试向量产生电路由一个n(n<m)触发器单元的LFSR和一个用于存储种子的片外或片上的只读内存器(Read Only Memory,ROM)构成,如图1所示。其中hi(i=1,2,…,n-1)表示反馈线的接通情况,若hi=1则表示反馈线接通;若hi=0则表示不接通反馈线。控制电路从ROM中周期性地向LFSR装载种子,由种子产生被测电路(Circuit Under Test,CUT)期望的确定性测试向量。
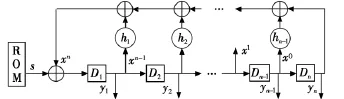
图1 n位的LFSR示意图Fig.1 The sketch map of n bit LFSR
若假设 y1(i),y2(i),…,yn(i)为 n 位寄存器 A1,A2,…,An在i时刻状态的输出值,而y1(i+1),y2(i+1),…,yn(i+1)表示LFSR输入一次时钟信号后在i+1时刻状态,则输出向量Y={y1,y2,…,yn}在时钟前后输出下应有关系
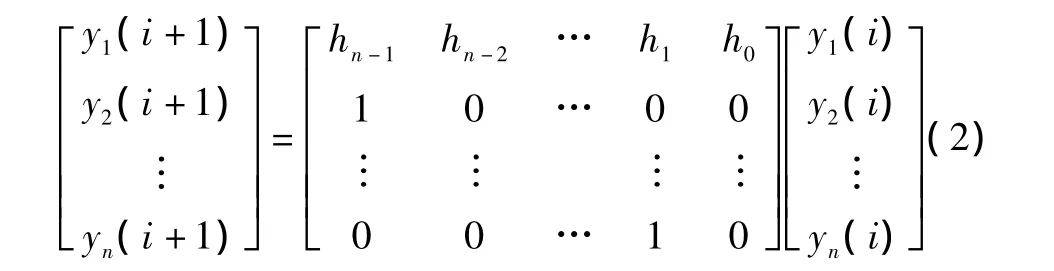
若假设LFSR的初始状态为0状态,从ROM中输出的种子序列为 s={s1,s2,…,sk},则 y1(1)在 i=1 时刻输出的值为;在i=1 时刻LFSR输出的测试序列为y(1)={y1(1),y2(1),…,yn(1)}=。
由于文中测试序列计算均是模2运算,且y(1)中仅s1是未知量,故简记为函数y1=f(s1),则y(1)={f(s1),y1(0),…,yn-1(0)}。
在第二个时钟周期输入s2后可知
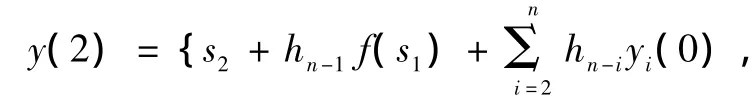
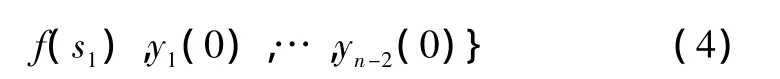
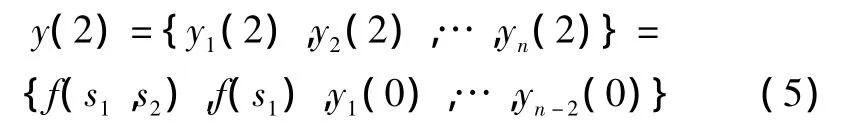
同理推论可知,在n个时钟周期后,LFSR的输出序列为

此时若假定被测电路期望的一个测试输入序列为z={z1,z2,…,zn},则
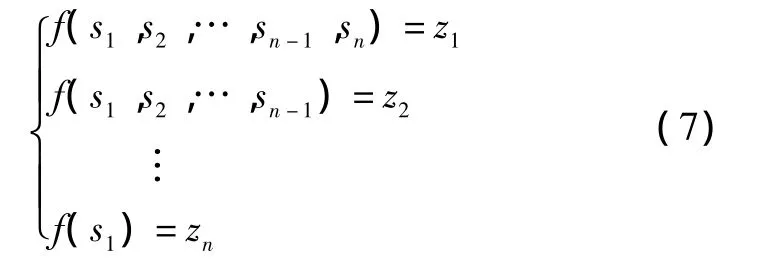
此方程是一个模2运算方程组,有且仅有唯一解[9]s={s1,s2,…∈(0,1),i∈(1,2,…,n )}。该方程组解的含义是,通过ROM中产生的种子序列都可以使LFSR从某个无关输出序列跳转到任意一个指定的输出序列z。若在第j(j<n)时刻LFSR的输出序列s=z, 则说明此时的输入种子即为方程组的解。
2 变周期重播种的伪随机测试生成
已经证明对于n阶的基于本原多项式的LFSR,只需要在其输入端输入m(m≤n)位的控制位,一定能够将LFSR中现有的测试矢量跳转到另一个指定的测试矢量。因此重复播种测试生成法针对随机测试的缺点,通过在ROM中存储序列生成的种子,此种子加载至LFSR后展开成所需的测试序列的思路来加快故障覆盖率的提高。但其生成的伪随机测试序列长度是不变的,即每次间隔相同的周期加载种子,其中包含较多的冗余测试序列,降低了测试加载效率。
在变周期重复播种测试序列生成中,每个种子所产生的伪随机测试序列长度通过一个模可变计数器来控制,跳过其无效冗余的测试序列。变周期重复播种测试生成结构如图2所示。

图2 变周期重复播种测试生成Fig.2 Generation of variable-cycle reseeding test
变周期重播种测试序列生成器包括一个模可计数器ROM和LFSR。与定长的重播种测试生成仅仅存储种子信息不同的是,在ROM中同时存储了种子S和序列长度信息L。
变周期重播种测试生成器的工作过程为:ROM将长度信息L和计算好的种子S分别加载到计数器和LFSR。在clk时钟信号的作用下,计数器开始计数,LFSR同时开始产生测试序列。当LFSR产生的序列长度达到预定的L长度的时候,计数器计满溢出,溢出信号控制ROM加载下一个种子到LFSR中,加载下一个序列长度信息到计数器中。这样每次在LFSR产生的测试序列长度达到有效测试序列的长度后,通过计数器的溢出控制信号来重新加载种子和序列信息,从而能有效地跳过冗余测试序列。其跳过冗余伪随机测试序列的原理如图3所示,图中,阴影部分为有效测试序列,空白部分为冗余测试序列。每个种子扩展后的长度序列可受计数器的控制,在其产生冗余序列之前,通过ROM加载的种子使序列跳转到下一段序列开始。这样每部分种子的测试序列长度将不一致,不再是以相同的周期加载种子,而是根据序列信息长度变周期地加载种子信息到LFSR。

图3 跳过冗余伪随机测试序列的原理Fig.3 The principle of skipping the redundant test patterns
以ISCAS85标准测试电路中选取的典型电路C880为例,通过对其分析可知,若采用4次播种的方式分组测试序列,则其序列长度信息如图4所示。

图4 C880电路测试序列长度信息Fig.4 The length information of test sequence in C880 circuit
变长重播种测试生成方法在其截取冗余测试序列的时候,未能有效截掉(2799,2816),(4032,4096)区间的冗余序列。由理论分析可知,在极端情况下,最大会有(L/4-1)长度的冗余序列不能被有效截掉,或是以丢失有效测试序列的代价来截掉冗余测试序列,这点从文献[10]中可以得到验证。
本文通过设计一个模可变计数器来控制种子的加载。由于对每个种子产生的序列长度信息从ROM中加载到计数器,在种子生成的序列长度达到预定的长度后,计数器控制ROM重新加载种子,从而能有效地跳过将冗余序列,加快测试序列生成的速度。
变周期重播种的LFSR结构测试生成的基本思想是通过计数器来控制种子生成序列的长度,从而跳过冗余序列。但是当每个种子随后生成的有效测试序列长度L分布不均匀,导致部分有效序列较长,部分有效序列较短,因此,计数器的最大计数模数必须满足序列中长度最大的一个,而在其他计数模式下以较小的计数模计数。当有效序列长度较大时,要求计数器的最大计数位数较多,从而造成计数器硬件开销过大。若通过在序列中增加种子的数量来缩短每个种子测试生成的有效序列长度,则会使存储种子和长度信息L的ROM资源消耗过高,因此需要合理分组测试序列,降低计数器的硬件开销。
3 实验结果和分析
变周期重播种测试生成方法选取ISCAS85电路中的典型测试电路。选取C880电路为分析样本,以便于与文献[10]测试生成方法做类比。其模拟分析结果如表1所示。
表1中:fcv表示故障覆盖率;fd表示检测到的故障个数;LD表示定长测试序列长度;LV表示文献[10]中采用的变长重复播种测试生成方法得到的测试序列;LE表示本文方法的测试序列。
由表1的结果可知,采用变周期重播种测试生成的方法通过计数器能很好地跳过冗余的测试序列(2799,3071),(4032,4095),(4096,5120),大大缩短了测试序列的总长度,缩短测试时间。相比于定周期重播种测试生成方法,总序列长度减少1357/5120≈26.5%,提高了测试效率。同时由于该方法能很好地保留有效的测试向量,保证其故障覆盖率不会下降。相比于文献[10]的方法其总测试序列长度也有一定的压缩。
事实上,该电路的测试序列减少还可以进一步地减少。由表1中的分析可知,在种子1开始,每个向量所能检测的故障个数开始明显下降,因此其第2,3,4组序列中还有进一步的分组可以减少的空间。理论分析可知,该电路的最小测试序列集长度小于其全部故障数994,如若能将全部的冗余测试序列长度跳过,则测试序列缩短幅度大于(5120-994)/5120≈80.59%,因此其测试序列缩短还有很大空间。
对ISCAS85和ISCAS89中的部分典型测试电路进行模拟分析,其测试序列长度都得到精简,结果如表2所示。
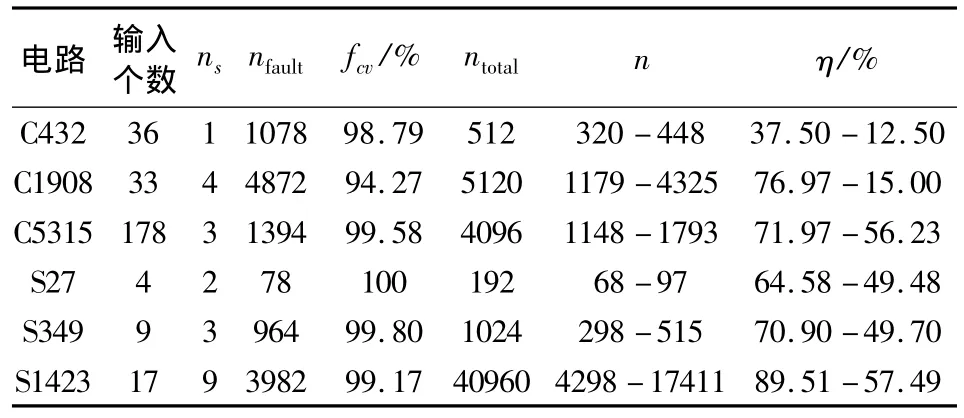
表2 ISCAS85和ISCAS89中典型电路模拟分析结果Table 2 The analysis result of circuit from ISCAS85 and ISCAS89
对比定长周期播种的测试生成方法可知,该方法是以额外的硬件消耗为代价的。如果分组越多,则能跳过的冗余序列越多,其测试效率越高,但是所对应的模可变计数器的硬件开销以及存储序列长度消耗的ROM存储的资源开销过大。例如,S27电路规模是21门,若采用该方法则计数器本身的硬件开销大于60门,此时此方法显然不具备可行性。若是分组过少,则会导致其中的冗余序列过多,改进效果不明显。因此在此方法针对实际电路运用时候,应该根据电路规模和测试复杂长度合理设计其BIST测试生成模块,以均衡硬件资源开销。
分析本文的方法可知,其计数器和测试序列长度信息存储均需要消耗一定的硬件资源,因此,对于小规模的电路而言,其硬件增加开销规模相对也会较大,在应用中不具有可行性。但是对规模较大的电路,其硬件的消耗的相对比例较小,而测试效率却得到大幅度提高,此时此测试方法是可行的。
4 结论
针对伪随机测试生成中包含的冗余测试序列较多测试效率不高的问题,提出了变周期重播种的LFSR结构的测试生成方法,利用模可变计数器来控制测试序列长度,并分析了其设计思路。然后运用该方法对ISCAS85和ISCAS89中的部分测试电路进行模拟分析。由分析结果可知,该方法在针对较大电路的时候,在保证电路的故障覆盖率的条件下,能以较少比例的硬件开销跳过冗余测试序列,减少总测试序列长度。对于一般较大规模的电路,其序列长度平均减少20%~50%,减少了测试施加时间,提高重播种测试效率。
[1]CHEN C,GUPTA S.BIST test pattern generators for two pattern testing-theory and design algorithms[J].IEEE Trans.on Computers,1996,45(3):257-269.
[2]WUNDERLICH H J.Accumulator based deterministic BIST.[C]//Proc.IEEE Int.Test Conf.Washington,DC.1998:412-421.
[3]ROTH J P.Diagnosis of automata failures:A calculus and a method[J].IBM J.Res.Develop,1966,10(7):278-291.
[4]GOEL P.An implicit enumeration algorithm to generate tests for combinational logic circuits[J].IEEE Trans.Compute,1981,30(2):215-222.
[5]向东.数字系统测试及可测性设计[M].北京:科学出版社,1997.
[6]LI Lijian,MIN Yinghua.An efficient BIST using LFSRROM architecture[EB/OL].[2005-10-12]http://ieeexplore.ieee.org/ie15/7181/19338/00893645.pdf.
[7]KAGARIS D.Multiple seed TPG structures[J].IEEE Transactions on Computers,2003,52(12):1633-1639.
[8]PROMERANZ I,REDDY S M.3-Weight pseudo random test generation based on a deterministic test set for combinational and sequential circuits[J].IEEE Trans.On CAD,1998,12(6):1050-1058.
[9]胡晨,许舸夫,张哲,等.一种基于受控LFSR的内建自测试结构及其测试矢量生成[J].电路与系统学报,2002,17(3):13-16.
[10]张建胜,黄维康,唐璞山.变长重复播种测试码生成方法[J].复旦学报:自然科学版,2006,45(4):517-522.
