曳引系统部件的直优设计
2012-07-04谢丽蓉加玛力汗库马什陈志军谢意龙
谢丽蓉,加玛力汗·库马什,陈志军,谢意龙
(新疆大学 电气工程学院,乌鲁木齐 830008)
0 引言
曳引系统各部件的配置与曳引力计算,有着极为密切的联系[1]。目前国内外常用的曳引计算,都是先按照单个约束条件,分别计算确定或按经验选定各影响参量,然后代入相应的张力比验算式中检验,若不满足防滑条件和打滑要求,则需重新调整某些参量的数值,以保证电梯安全运行[2,3]。该算法不能充分利用曳引能力,常常会使曳引配置的重量增大。文献[4]将曳引配置各部件的重量,均采用了曳引条件的防滑判据来计算确定,使各部件的计算数值,满足了防滑条件和打滑要求。因此,曳引配置就变成了包涵曳引条件各部件优化计算与选择,可以不需要进行防滑和打滑验算。这与目前国内外曳引计算常用方法有着本质的区别。
曳引系统各部件均为防滑判据的函数,如电梯的轿厢自重、平衡对重、曳引钢丝绳、曳引轮径等均为防滑判据的函数,为配置优化设计最优匹配提供了理论计算依据[4],同时实现配置总重量达到最小的目标。由于理论计算值与实际选用值有一定差异,配置的优化设计必须符合实际选用值的具体算法。例如:对重平衡系数大于计算值、轿厢自重大于计算值时,就需要进一步研究其实用性,便于工程计算时采用。
1 曳引系统配置优化设计
采用防滑判据直接来计算确定各部件,达到曳引配置总重量为最小的最优目标,采用直优设计方法配置系统各部件,以曳引系统电梯作为研究对象,按直优设计来完成系统的部件配置。
符号说明:曳引系统曳引绳悬高H0,额定载重QN(kg),运行最大高度H,采用曳引轮槽型为V型,半绕式系统围包角α。
1.1 速度合理选择
根据电梯合理速度的计算关系,同时还考虑楼内客流量以及其他因素来选定电梯的速度。
单台电梯按行程最大高度合理确定最大速度v为:
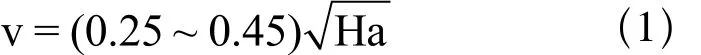
根据式(1),来选择标准速度。
1.2 防滑判据的确定
防滑判据就是静张力比的许用值,必须保证有足够的张力比静防滑安全系数,曳引能力与静防滑安全系数之比即是防滑判据,也是静张力比的最大许用值[5,6]。防滑判据[c]为:

1.3 配置各部件和防滑判据的函数关系
1)轿箱自重
从曳引条件的要求出发,轿箱自重有两个值,一个是防滑最小自重,另一个是打滑最小自重,轿箱自重应不小于这两个最小自重[4]。
两个最小自重的判据式为:


根据式(3)或式(4),选取轿箱自重系数βz,确定轿箱自重质量Qz。
2)曳引绳
(1)n根绳每米质量np
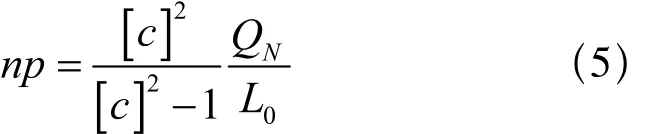
(2)每根每米绳重质量Q
当选定n时,p便可知,在钢丝绳产品目录中选取满足要求的,同时可查得σ、d,计算出:

(3)安全系数校核
根据安全系数m,校验安全系数是否符合(6)式要求[4]。

(4)重算L0及h0
若曳引绳安全系数m符合要求,即大于最小许用值,将使L0减小,h0增大,故需重选L0和
3)曳引轮直径
曳引轮直径D应小于曳引绳径d的40倍[1],为了获得曳引轮直径与防滑判据的函数,可以借助于曳引绳每米重p与防滑判据的关系,曳引绳径d与每米重p之间存在着一定的几何物理关系,从8X19S+NF技术数据中,可找到一个比例常数[7],纤维绳芯,kd=17.17。曳引绳径d为:
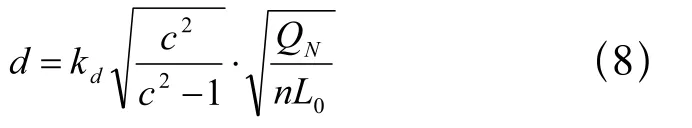
4)曳引轮两侧静张力比
由于轿箱自重略大于计算值,而且曳引绳安全系数亦大于最小值,所以会使曳引轮两侧静张力比略小于防滑判据[4]。
5)对重平衡系数
对重平衡系数为:

6)超载试验系数
为了验证曳引能力是否能达到计算的数值,最后应通过超载试验系数来检验,以确保曳引电梯的安全性。超载试验系数为:

1.4 曳引验算再检验
以上计算,是能够保证曳引条件的防滑和打滑要求的。
进一步证实或再检验[6]:
制动工况应符合防滑条件,防滑检验

滞留工况应符合打滑条件,打滑检验
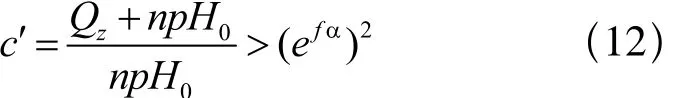
2 应用实例
某高层建筑的客梯,曳引绳悬高H0=71(m),额定载重QN=1000(kg),运行最大高度H=65(m),采用曳引轮槽型为V型,γ=42°,半绕式系统围包钢丝绳,双强度的,曳引绳静安全系数m=12,根数n=4,采用直优设计方法配置电梯各部件,方法如下:
1)速度合理选择
2)防滑判据的确定
曳引能力 efα=2.076,
3)轿箱自重的确定
h0=0.0644,但它小厢自重应按防滑条件计算。

4)曳引绳计算与选择
(1)n根绳每米质量
(2)每根每米绳重质量
(3)安全系数校核
m=12.45>12,符合要求。
(4)重算L0及h0
曳引绳安全系数m>12,即大于最小许用值,故会使L0减小,h0增大,L0=1062m,h0=0.0668m。
5)曳引轮直径
dN=8.345mm, DN=333.81mm, d*=D*=1.5564,d=12.97mm, D≥519mm。
曳引绳径的计算与曳引绳重的计算选择值,完全一致。
6)曳引轮两侧静张力比
轿箱自重略大于计算值,曳引绳安全系数亦大于最小值,会使曳引轮两侧静张力比略小于防滑判据。
7)对重平衡系数:kp=0.4342
8)超载试验系数: xmax=0.4342
为了验证曳引能力是否能达到计算的数值,最后应通过超载试验系数来检验,以确保曳引电梯的安全性,如果曳引能力efα中应留有1.1的动防滑安全系数的话,那么xmax=2.1。
9)曳引验算再检验
c=1.305<[c]=1.305,符合防滑条件;c'=8.449>(efa)2=4.31,符合打滑条件。
3 对重平衡系数两种算法对电梯配置的影响
对重平衡系数的算法有两种:第一种算法是空、满载时静张力差相等,曳引转矩较小,拖动功率较小,kp=0.5;第二种算法是空、满载时静张力比c相等,且均等于防滑判据,曳引传动安全性高,曳引配置总重量最小,kp=0.4~0.45。曳引电梯宜采用第二种方法较为合适,故称kp=0.4~0.45为最优平衡系数。
第一种算法的平衡系数,由于kp与其他因素有关,简单方便,常用于理论分析。第二种算法,由于它与实际参数有关,既与防滑判据有关,又与轿箱自重和曳引绳悬高有密切的关系,故在实际的电梯系统设计中,常常被采用,但过去没有准确简单的计算关系,文献[4]给出了简洁的公式来描述,这样就便于在实际工程计算时,更准确容易的被采用。
对重最优平衡系数、轿厢最小自重系数分别为式(8)和式(3)。
当k'p>kp时,按空载时静张力比计算,轿厢最小自重系数为

当k''p<kp时,按满载时静张力比计算,轿厢最小自重系数为

在[c]及h0为常数时,β'zmin随k'p增加而增加,β''zmin随k''p减小而增加,两条直线的交点,就是βzmin,而且是最小值,此时的kp便是最优值。
例如:[c]=1.3,h0=0.1时βzmin=1.2044;当 k'p=0.5>kp,β'zmin=1.4;k''p=0.4<kp,β''zmin=1.34。
这就说明,当平衡系数大于或小于最优平衡系数时,轿厢自重均会增大,曳引绳重增大,对重增大,曳引轮两侧悬重增加,只有在最优平衡系数时,曳引绳两侧总悬重才是最小的。
防滑判据一定时,两种算法不同,得到的对重平衡系数也将会不同,表1中给出了对重平衡系数取值的不同,对电梯配置的影响。
由表1中数据可以看出:当采用空、满静张力比相等原则与空、满静张力差相等原则,分别设计出曳引配置结果,在实例特定条件下,后者比前者:轿厢自重增加18.1%,对重增加17.3%,空载时两侧悬重增加15.9%,厢重与绳重之比增加18.4%,超载试验系数增加15.7%,而曳引绳静安全系数却降低9.4%。为了满足曳引绳安全系数的要求,有时则需要提高一级钢丝绳的抗拉强度,或提高一级曳引绳直径,或增加曳引绳的根数,才能满足要求。由此可见,如果平衡系数kp=0.5,可使转距和功率较小,但从曳引条件出发和曳引配置总重量来看,就产生了上述缺点。对重平衡系数kp=0.4~0.45时,曳引配置总重量为最小。

表1 对重平衡系数两种算法对电梯配置的影响
4 结论
1)曳引系统部件直优设计,克服了传统算法凭经验试验算法的缺点,采用了防滑判据来计算曳引配置的各部件,理论系统性强,已形成一套完整的设计程序;
2)当理论计算值与实际采用值出现差异时,在设计中均能得到修正,如曳引绳重大于计算值,会使曳引绳安全系数大于规定最小值,即L0减小,h0增大;轿厢自重大于最小值时,这二者的差异均由静张力比变小来修正;平衡系数大于最优平衡系数时,则用空载状态下轿厢最小自重来修正;平衡系数小于最优平衡系数时,则用满载状态下轿厢最小自重来修正;
3)目前采用的对重平衡系数,常大于最优平衡系数,这样将使轿厢自重增大,曳引绳两侧悬重增大,增大了所有材料的消耗量,同时曳引绳的安全系数降低,为了满足曳引绳安全系数的要求,曳引配置的成本就会提高,所以,对重平衡系数,应以空、满载静张力比均等于防滑判据的原则来确定最为合适。
[1] 全国电梯标准化技术委员会.GB 7588—2003 电梯制造与安装安全规范[S].北京: 中国标准出版社,2003.
[2] Carlo Distaso, 著, 裔振勇, 译.曳引力计算[J].中国电梯, 2001, 12:23~27.
[3] 陈彬.曳引力计算示例[J].中国电梯, 2001, 1: 30~32.
[4] 谢丽蓉.电梯曳引计算的优化方法[J].机械设计与研究, 2008, 3: 113~115.
[5] 谢意龙.曳引电梯与防滑判据[J].中国电梯, 2001, 9:58~62.
[6] 谢丽蓉, 王智勇.曳引系统曳引计算的研究[J].矿山机械, 2007, 12: 73~75.
[7] 毛怀新.电梯与自动扶梯技术检验[M].北京: 学苑出版社, 2001.
