基于交流调制的光栅干涉条纹信号的细分技术及实现

储玉芬

（闽西职业技术学院 电气工程系，龙岩 364021）

0 引言

精密测量系统是仪器仪表、超精密加工、微型机电系统等制造领域发展的基础。目前该领域应用较广、发展比较成熟的主要有激光干涉类位移传感器和栅尺类位移传感器，其测量原理都是通过对位移引起条纹移动的处理分析来实现位移的测量，一个周期的条纹信号代表一个栅距的位移或半个激光波长λ的位移[1]。在精度要求不高时,只需计算此信号变化的周期数,即可求得光栅尺的相对位移[3]。但是,随着科学技术的发展，对光栅信号的周期进行计数远不能满足精密测量和加工的需要[2]，要达到更高的精度，就需要对光栅信号进行细分处理。传统的细分方法是通过硬件电路来实现的,随着精度的提高，对细分数的要求提高,往往需要大量的元器件，复杂的工艺来完成[4]。而软件数字细分方法，常常由于采样的速度、时间和稳定性的限制，难以达到大的行程范围，并常伴有采样信号不稳定，误差大、与硬件信号难以同步等问题。

本文针对以上情况，采用硬件细分与软件细分相结合的方式，设计了一种长行程、高精度的衍射光栅位移测量系统。该系统以衍射光栅作为计量基准，采用FPGA对光栅的干涉条纹进行硬件细分，具有高精度，响应快，体积小，稳定性好等特点；使用上位机编程对采集卡高速采样的光栅信号进行软件细分，并针对硬件细分与软件细分不同步等问题进行了补偿，提高了测量范围和精度。最后使用高精度的双频干涉仪对测量结果进行比对验证，达到了较高的精度。测量系统的原理框图如图1所示。

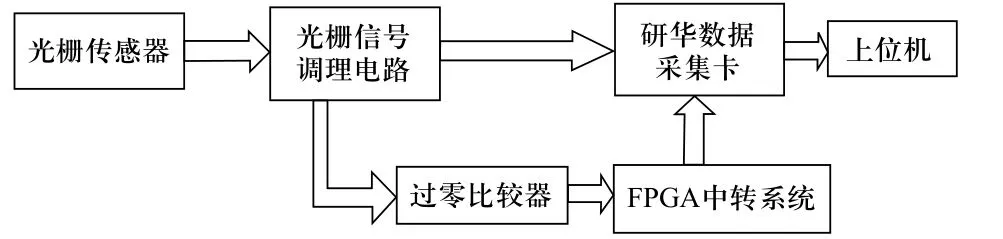
图1 光栅测量系统原理框图

1 光栅信号的接收和交流调制

实际的信号接收效果表明，对于圆形干涉条纹，采用田字形光电传感器获得的差分信号较稳定，并且参数一致、对称性好。

光电管分布方式如图2所示。

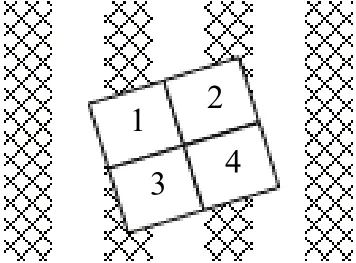
图2 光电管接收信号的分布方式

输出的两路差分信号为：

可以看出，若使用传统的直流光源，当条纹静止时，sinθ，cosθ为常数。由背景光强等导致的直流噪声C难以消除，因此，采用在直流的基础上引入高精度的交流信号给激光器供电。加在激光器两端的电压为 。输出的两路差分信号为：

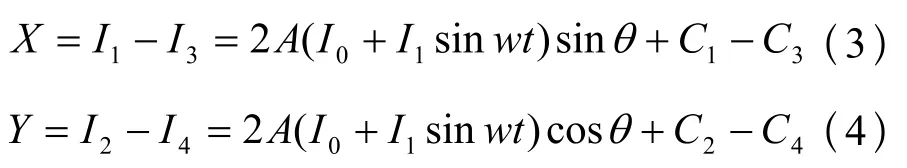
当工作台运动时，该信号实际采样结果如图3所示。

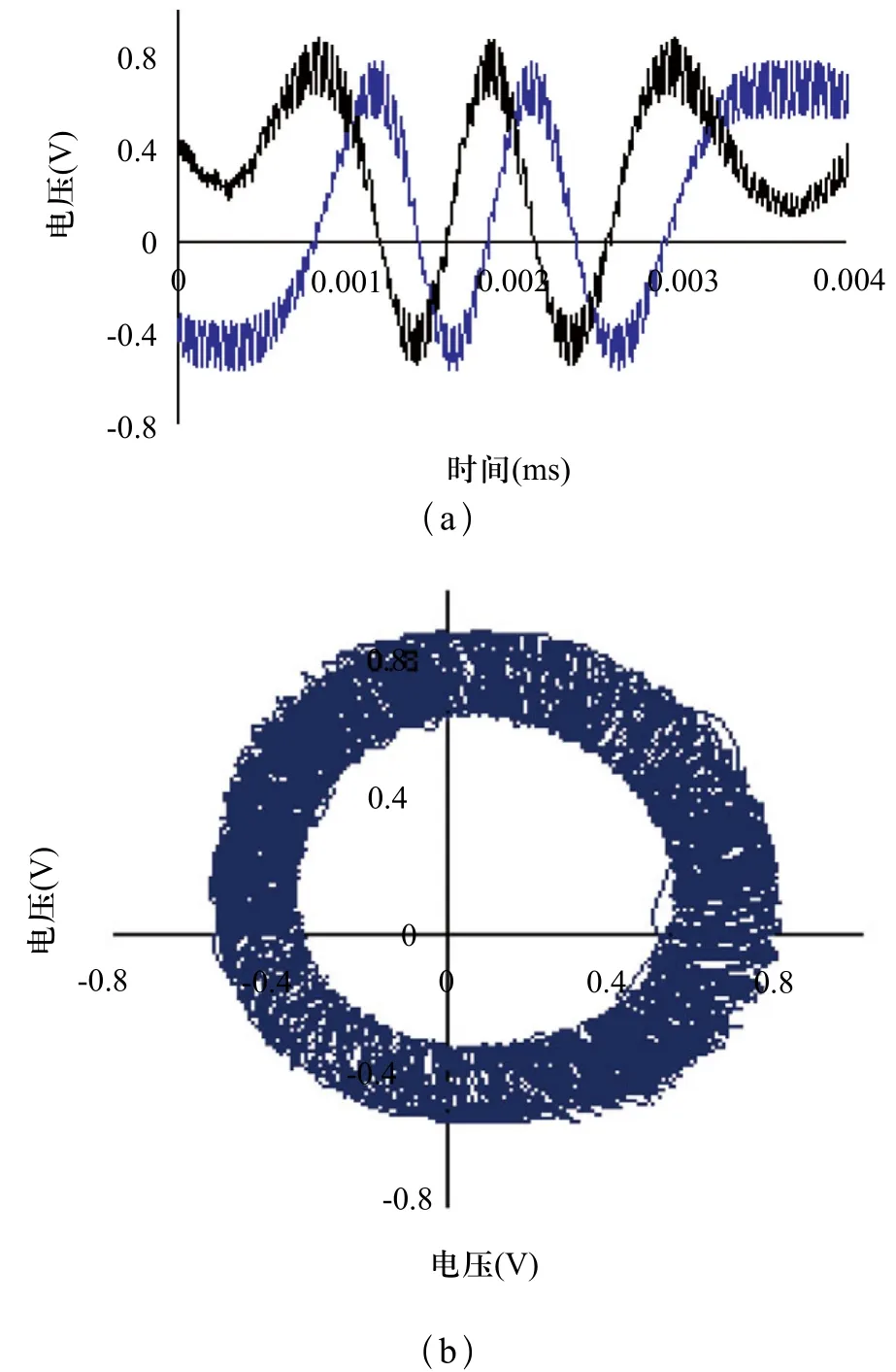
图3 实际采样的两路光栅信号

对这两路信号作以下两种处理，1）将X、Y经过零比较后输入FPGA进行一系列运算，得出硬件计数值；2）对其进行滤波和检波等处理，用于软件细分，具体方法如下。

X'与Y'两路信号通过数据采集卡高速采样，用于上位机的软件细分。

2 硬件计数值的获取

干涉条纹每个周期四倍锌粉是由FPGA编程实现的。将差分信号过零比较后，由FPGA对其进行辨向及计算出位移计数值，传递给上位机。

设A、B为X、Y经过过零比较后的两路数字信号，代表两路信号的极性。假设光栅信号在穿越某个象限的瞬间，A、B的前一种状态分别为A1、B1，动光栅尺朝两个方向移动的辨向细分脉冲分别为 P+、P-，则硬件四细分的计数逻辑为：

FPGA内部的光栅辨向计数模块如图4所示。

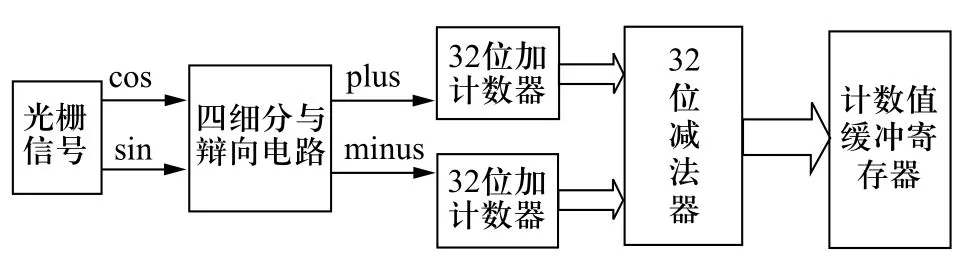
图 4 FPGA内部辨向计数模块

对脉冲的计数方法如图4所示，四细分与辨向电路用于实现式（7）中正向和逆向的计数逻辑，两个加法计数器记录下两个方向的累计位移计数值，再由减法器相减得到总位移计数，将所得结果由数据采集卡传递给PC机。实验采用600线光栅尺，光栅信号每跨越一个象限，计数值加1或减1，光栅尺的位移变化1/2400mm。

3 软件细分与补偿

为得到更高的精度，必须在四细分基础上由上位机进行软件细分。用于软件细分的两路信号如图5、6所示，所设计的虚拟仪器界面显示出高速采样的两路动态光栅信号及其李萨茹图。

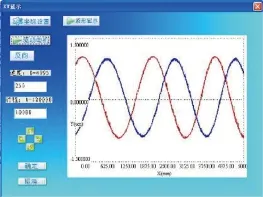
图5 两路动态光栅信号

图6 两路信号李萨茹图

3.1 软件细分方法

结合硬件细分得出的大位移值，可对信号进行进一步细化，计算出信号在该象限内的小位移量，通过获取信号在该象限内走过的角度来完成。具体方法如下。

设信号顺时针为正向、逆时针为负向，由于光栅计数值代表的位移方向与细分位移方向相反，故先将光栅计数值取反。用于软件细分的两组信号分别为x,y，计算出信号在该象限内正向移动的角度。

实验采用600的光栅尺，则根据小位移值θ和硬件计数的大位移值可求出总位移：

3.2 硬件与软件细分信号不同步的补偿方法

理想状态下，硬件计数与软件细分所采用的信号是同步的，均处于同一象限，但经实验分析，由于信号调理电路非对称性、干扰噪声，交流调制后的信号的直流和交流部分响应速度不同等影响，硬件计数与软件细分，难以严格同步，存在一个100ms左右的时间差，从而导致两组信号存在相差，但由于时间差很短，因此工作台动光栅移动的最大速度下，该相差也不可能超过一个象限。如图7所示，当产生一个微小位移时，信号由第四象限移动到了第一象限，此时，计数值应发生跳变，由初始状态的0变为1。但由于相差的存在，可以看出硬件计数值仍停留在第四象限，在这样的情况下，就必须对硬件计数值进行补偿。

采用以下方法进行补偿，用VC++编程实现。

在先确定位移初始位置时计数值在每个象限的理论值， 测量位移发生改变时，无论信号经过多少个周期，到达同一象限时，其计数值对4的余数均不发生变化。若测量结果显示其硬件计数值对4的余数与理论不符，且由于误差不超过一个象限，则对其做加1或减1的修正，由此方法来校正硬件计数值。采用的补偿方法如下：

若{硬件计数值-( R-I+C )%4+4}%4=1；则计数值减1；

若{硬件计数值-( R-I+C )%4+4}%4=3；则计数值加1。

其中，R为实际测量时所得计数值对4的余数，I为信号的初始象限，C为当前信号象限。图7(a)所示为补偿实验截图，信号在第四象限时所测得的硬件计数值为0。当信号沿逆时针移动至第一象限的X轴附近时，如图7(b)所示，理论上计数值应跳变为1，而实际测量时硬件计数值仍为0，应由软件将其补偿至1，图中“光栅计数值（软件）”显示的即为补偿后的计数值。

4 实验验证

图7 光栅计数值软件补偿实验

将以上硬件与软件相结合的细分方法，实现在衍射光栅位移测量系统上，驱动实验工作台移一段距离，图8(a)为光栅测量的结果。其中“0通道”“1通道”显示的值分别表示用于软件细分计算的X、Y轴的信号均值，“细分”显示值即为最终的测量总位移。而此时信号均值处于X轴附近，图8(b)表示，此时的计数值经过了补偿。

图8 光栅测量实验结果

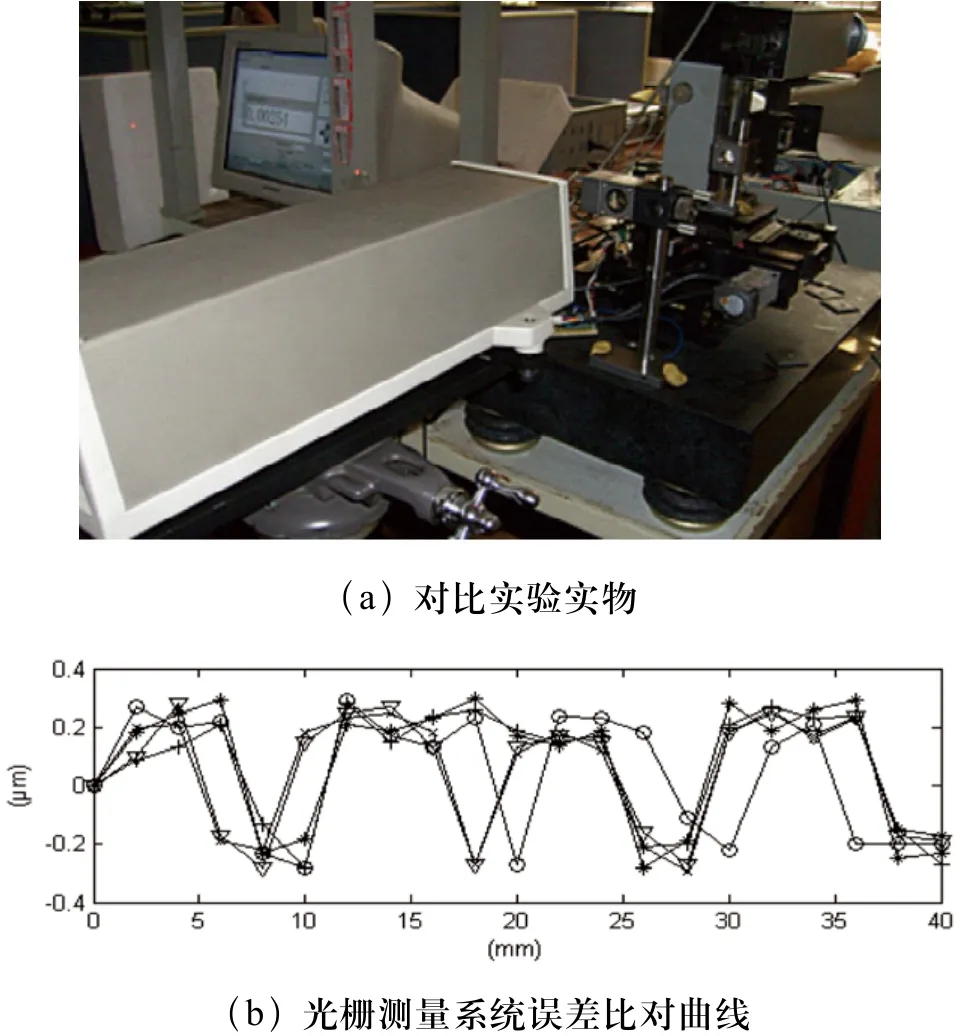
图 9 测量系统与双频干涉仪的误差比对实验

将该测量系统与双频干涉仪的进行比对，测量系统范围为40mm，测量工作台每次左右移动2mm，进行了五次实验，图9（b）显示了相对双频干涉仪的示值误差。光栅测量系统的最大示值误差为±0.30μm，标准差为0.2045μm。

5 结束语

本文提出的细分技术经验证达到了良好的效果。交流调制技术可以获取较好的信号用于硬件计数与软件细分，并且避免了直流漂移现象，减少了环境噪声的干扰。用FPGA设计的中转系统实现硬件四细分，具有较高的工作频率，并且稳定性好，保证了软件细分需要的大位移值。上位机软件细分解决了硬件不能达到高精度的问题，并且对产生的误差进行了补偿，实验证明，该测量系统具有较高的精度，能满足精密测量的需要。

[1] 刘晓军, 宋浩. 基于偏振相移的干涉条纹细分原理[J]. 华中科技大学学报, 2008, 36(6): 4-6.

[2] 李怀琼, 陈钱. 新型光栅信号数字细分技术及其误差分析[J]. 计量学报, 2001, 22(4): 281-283.

[3] 唐晖, 叶险峰. 一种基于FPGA的光栅莫尔条纹数字细分技术[J]. 计量技术, 2006(10): 14-17.

[4] 蔺小军, 史耀耀. 光栅信号软件细分技术及其误差分析[J],工具技术, 2006(10): 72-74.

[5] 苏红. 光栅尺位移测量仪表的研究[D]. 西北林业科技大学, 2008.

[6] 罗华, 高山. 粗光栅信号全数字化处理法实现高倍数细分[J]. 光学精密工程2007, 15(2): 283-288.