汽车操纵稳定性的时域分析

公伟强，高树健，陶斯祺

Gong Weiqiang, Gao Shujian, Tao Siqi

（长安大学汽车学院，陕西 西安 710064）

0 引 言

伴随着社会和高速公路技术的飞速发展，人们对汽车行驶速度的要求越来越高，使汽车在高速行驶时的操纵稳定性变得尤为重要。驾驶员都希望所驾驶的汽车比较好“驯服”，即可以按照他们发出的指令正确行驶，同时也能给予驾驶时的舒适感。

对于汽车操纵稳定性的评价大体可分为两大类[1]：力输入反应特性与角输入反应特性。汽车的转向是靠驾驶员作用在转向盘上的力，使转向盘转过一定角度，进而控制汽车转向。

MATLAB/Simulink模块的输入方式可以使一个复杂的数学仿真问题变得直观而且容易实现。采用 Simulink以前轮转向（2WS）与四轮转向（4WS）典型的二自由度汽车模型为例进行仿真，不仅对横摆角速度和侧向加速度做出分析，而且通过一种总方差计算方法评价了汽车的综合操纵稳定性能。

1 汽车模型的建立

1.1 2WS汽车模型的建立

为了便于掌握操纵稳定性的基本特性，将所研究的汽车简化为二自由度模型，即只考虑横向平移和绕轴的横摆运动[2]，如图1所示。令车辆坐标系的原点与汽车质心重合，由牛顿第二定律得到2WS二自由度汽车运动微分方程

1.2 4WS汽车模型的建立

为了得到便于分析和研究的方程式，将所研究的4WS汽车简化成二自由度模型，分析时所作的假设与上述2WS模型简化相同（如图2），进而得到4WS汽车线性二自由度模型的运动微分方程式[3]

其中，δ1,δ2为前、后轮输入转角。

2 动态反应误差的总方差评价

把汽车转向行驶看做一个开环控制系统（如图3），x（t）代表驾驶员给出的指令，y（t）代表系统的输出，即汽车的转向反应，该输出包括横摆角速度、侧向加速度、侧偏角等。则该系统的反应误差表示为：

其中，y0为系统输出y(t)的稳态值。

3 MATLAB/Simulink环境下的 仿真

根据上述所推导的汽车模型方程式，在MATLAB/Simulink环境下建立仿真模型[4]。仿真时，忽略驾驶员的反应时间，即前轮转角δ，δ1和后轮转角δ2均采用起跃时间为零的单位阶跃函数作为输入，其中其余仿真参数如表1所示。

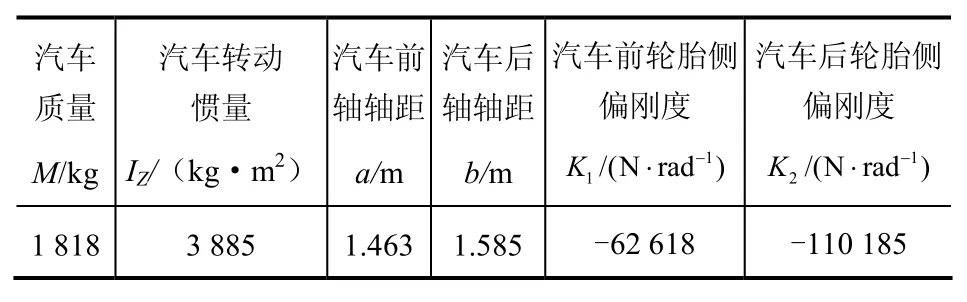
表1 仿真模型参数

为了便于比较，选择20 km/h与60 km/h两种转弯速度，利用以上仿真参数在 MATLAB里编辑.m文件，运行Simulink模型，可以得到横摆角速度与侧向加速度的时域响应图像，如图4、图5所示。

从图4，图5中可以看出，无论是低速转弯（20 km/h）还是高速转弯（60 km/h），过渡时间（达到与指令值接近，即系统达到稳态，误差小于±5%的时间）基本相同。

低速转弯时，两种转弯方式的超调量（最大峰值与稳态值之差）相差不大，难以区分其在低速转弯时的操纵稳定性能。而在高速转弯时，前轮转向汽车的横摆角速度与侧向加速度的超调量都远远大于四轮转向汽车的超调量，这使驾驶员在高速转弯时难以操纵汽车。

从图 4，图 5难以区分两种转弯方式在低速转弯时的性能差别，所以采用总方差评价方法进一步评价两种转弯方式的操纵稳定性。由于仿真时采用单位阶跃输入，故系统输入x（t）≡1，输入稳态值x0=1，故式（5）变为

取车速 20 km/h，40 km/h，60 km/h，80 km/h，100 km/h，120 km/h，按照式（6）利用MATLAB进行仿真计算，得到两种转弯方式不同车速下的系统误差总方差，见表 2，并且利用MATLAB对数据进行3次样条插值，得到平滑曲线（见图6）。

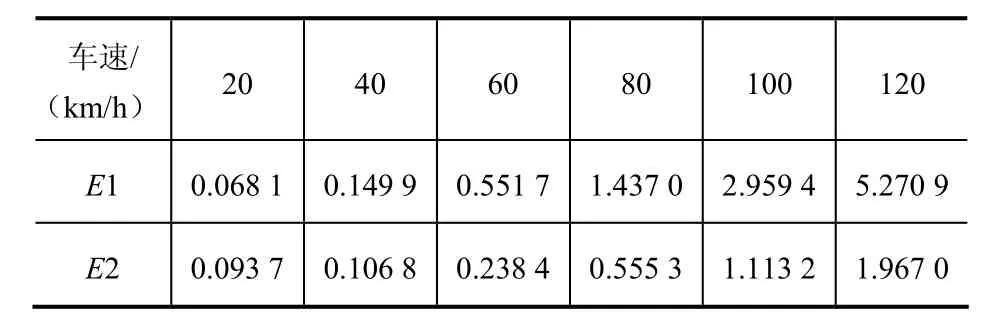
表2 不同车速下的总方差

从图6中可以看出，在约25 km/h车速下，四轮转向汽车的系统总方差略大于前轮转向汽车，即低速时，前轮转向汽车可以更好地保持驾驶员指令输入与车轮转向角度输出的一致性，汽车更容易被“驯服”。随着车速度增高，四轮转向汽车的系统输入输出的一致性越来越优于前轮转向汽车。

比较两种评价方法可以看出，系统误差的总方差法可以更直观的表现出不同转向方式汽车在响应驾驶员指令一致性上的不同，弥补了横摆角速度等时域响应方法对汽车低速转弯时性能评价的不足。

4 结束语

利用 MATLAB/Simulink模块，建立了两种不同转向方式的二自由度仿真模型，比较了两种不同评价方法，得到以下结论。

（1）MATLAB/Simulink模块在汽车上的应用，使得分析问题时更加直观形象。

（2）在该仿真模型中，汽车低速时采用前轮转向操纵稳定性略优于四轮转向方式，而在高速时则相反，随着车速增高表现得越来越明显。

（3）系统误差总方差评价方法在评价简单汽车模型操纵稳定性上更加直观、准确。

[1]王德平，郭孔辉，宗长富.车辆动力学稳定性控制的理论研究[J].汽车工程，2000，22（1）：7-9.

[2]余志生. 汽车理论（第3版）[M]. 北京：机械工业出版社，2001.

[3]郭孔辉. 汽车操纵动力学[M]. 长春：吉林科学技术出版社，1991.

[4]黄忠霖. 控制系统MATLAB计算及仿真[M]. 北京：国防工业出版社, 2004.