ICPSO算法及其在经济负荷分配中的应用
2012-07-02辛建涛方仕勇林锦钱
邹 恩,辛建涛,方仕勇,林锦钱
(华南农业大学工程学院,广州510642)
经济负荷分配ELD(economic load dispatch)是电力系统中典型的一类数学优化问题,由于它具有复杂、非线性、不连续等特点,已成为电站经济运行的重要优化问题。目标是在满足系统负荷和运行约束条件的前提下,在一个电厂或电力系统内合理安排各机组的出力负荷,使发电成本最小化,以降低燃料的消耗和供电成本。
在解决ELD问题上,由于火电机组存在阀点效应[1],加之系统运行约束条件、稳定性等制约,致使系统本质上成为非凸的高维、非线性以及不连续的优化问题,因此在寻求机组最优组合解的过程中将会存在复杂性及准确性的问题,甚至很难得出理论上的最优解[2]。由于ELD问题具有很强的实用性和经济性,自始至终都有大量的学者对其进行研究,目前为止已有很多文献涉及到此类问题的求解,如常规算法有线性规划法[3],动态规划法[4]以及拉格朗日松弛法[5]等,智能算法有遗传算法[1,6,7]、蚁群算法[2]、神经网络算法[8]以及混沌优化算法[9,10]等。然而这些算法在处理ELD问题上,都存在一定的缺点,如容易陷入局部最优、求解精度不高、容易陷入“维数灾”以及计算时间较长等。
粒子群优化算法是一种新的模仿鸟类群体行为的全局智能优化算法,现已成为进化算法中一个新的重要分支。由于算法操作简单、收敛快、且易于实现等特点,得到了广泛的关注,并已成功运用于求解不同领域的多维非线性优化求解中。然而粒子群算法在搜索后期容易陷入局部最优,发生“早熟”现象。针对这一缺陷,已有许多学者对其进行改进,一是对粒子群算法本身进行改进[11,12],增强粒子的全局寻优能力;二是粒子群算法与其它算法如单纯形法、遗传算法、混沌优化等算法相结合[13~16],利用各种算法的优势互补进行求解。
以往的混沌粒子群优化算法是在粒子群算法陷入局部极值后通过引入混沌扰动,使其跳出局部最优。本文在文献[17]的基础上,通过修正粒子群迭代的行动策略,并在粒子群寻优过程中引入Tent映射增强粒子的全局遍历性,以实现更快的收敛效果。与前者相比,后者有更好的收敛性能。最后将本文改进的混沌粒子群算法应用在电力系统经济负荷分配中,仿真结果体现了ICPSO算法的有效性和优越性。
1 经济负荷分配的数学模型
1.1 目标函数
发电机组燃料消耗的目标函数模型如下所示:
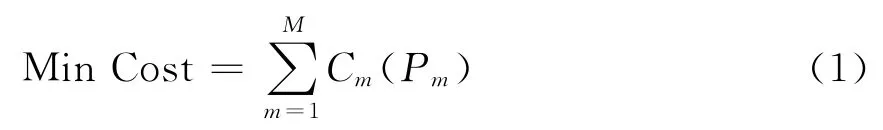
式中:Cost为发电机组总的消耗费用;M为系统发电机总数;Pm为第m 台发电机的有功功率;Cm(Pm)为第m台发电机的耗量特性,表达如下:
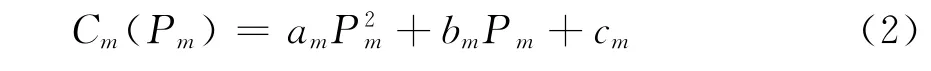
式中:am、bm、cm为第m 台发电机燃料消耗特性曲线参数,均为一常数。
在火力发电机组运行中,气轮机进气阀突然开启时常常产生阀点效应,增加发电机的出力,使发电成本增大。阀点效应耗量特性可表示为

式中:Em为阀点效应引起的耗量特性;gm、hm和分别为第m台发电机的参数和有功功率下限,gm和hm均为一常数。
1.2 约束条件
1)发电机出力运行约束

式中:Pminm、Pmaxm分别为第m 台发电机的出力上下限值。
2)系统有功平衡约束

式中:PL和PD分别为系统的总网损和总负荷。
网损可以采用潮流软件获得,工程上习惯用B系数法进行求解[8]。网损与发电机有功功率之间的关系表达式如下:
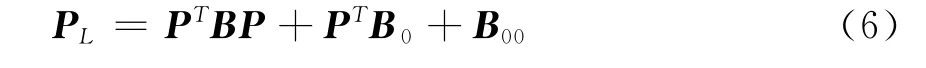
式中:PT为P的转置向量,其中P为发电机有功功率的m维列矢量;B为m×m维方阵,B0为m维列矢量,B00为一常数值。
2 改进的混沌粒子群算法ICPSO
2.1 混沌粒子群CPSO算法及其改进
传统的混沌粒子群算法是针对粒子群算法后期收敛慢,且容易陷入局部最优等缺点而提出的,基本原理是在粒子群算法寻优后,通过引入混沌机制,利用混沌运动的遍历性、随机性以及规律性,对其近似最优解进行混沌搜索,使其跳出局部最优而获得全局最优解。
2.1.1 Tent混沌映射
Tent映射是一种遍历性、随机性都很强的混沌映射,具有区间均匀搜索特性。其表达式为
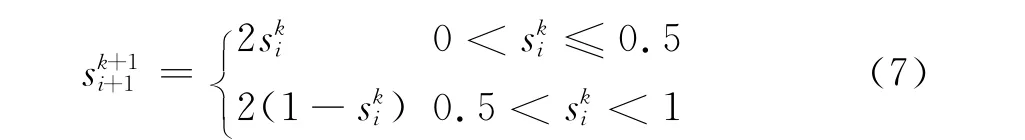
2.1.2 改进的粒子群算法
对于基本粒子群算法,迭代更新公式如下:
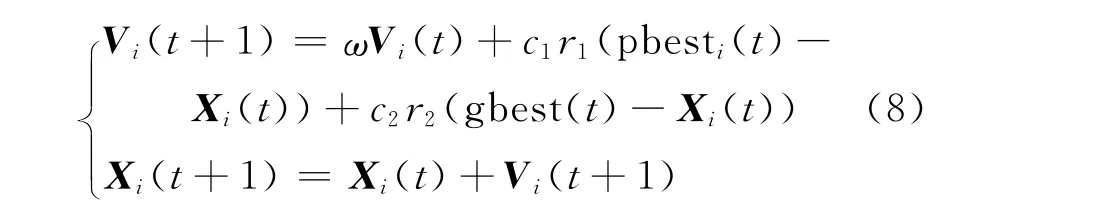
式中:Vi(t)= [vi1,vi2,…,viN]和 Xi(t)= [xi1,xi2,…,xiN]分别表示第i个粒子的速度和位置矢量;t为当前的迭代次数;ω为惯性权重;c1和c2是学习因子,通常取c1=c2=2;r1和r2是介于(0,1)之间的随机数;pbesti和gbest(t)分别表示第i个粒子迭代t次所经历过的最优位置和整个种群经历过的最优位置。
由于粒子群优化算法中每个粒子是根据当前个体极值和全局最优解来更新下一代的信息,没有考虑其它粒子的信息,因此,可选取前n个粒子的信息来修正每个粒子下次迭代的行动策略,在更新中可实现种群粒子搜索的多方向性,搜索更均匀,提高了算法的全局寻优能力[12]。由此粒子群更新公式可写为
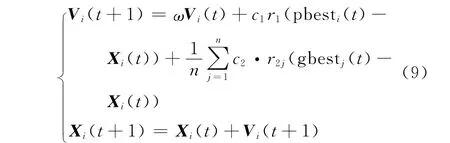
式中:r2j是(0,1)内的随机数;gbestj(t)是根据种群所有粒子的适应度值按从小到大排序后选取前n个粒子在解空间中的位置,一般n的取值为4时算法能取得较满意的效果[12]。
对于惯性权重ω,可采用非线性动态惯性权重系数公式即自适应权重法,以改善粒子的全局搜索能力和局部改良能力,其计算方法如式(10)所示:

式中:ωmax和ωmin为ω的最大和最小值,分别设为0.9和0.4;f是当前粒子的适应值,favg和fmin分别为当前所有粒子的平均适应值和最小适应值。
2.2 ICPSO算法在ELD问题中的应用
由机组组合数学模型可知,发电机组产生的费用由机组燃料消耗和阀点效应产生的费用组成,对发电机出力运行约束式(4),机组变量需限制在出力范围内,对于越限分量将其限制在边界值上。对于系统有功平衡约束式(5),可采用罚函数的形式将有约束问题转化为无约束优化问题,最终目标函数如式(11)所示:

式中:ξ为罚因子,通常取一个较大的常数;对于每个粒子Xi的值,代表了所有发电机出力负荷[pi1,pi2,…,piM]的一组解,即如式(12)所示:

ELD问题的ICPSO算法基本流程如下:
Step 1 设定粒子群体迭代次数max_gen、混沌局部搜索次数max C,以及群体规模D,初始粒子位置Xi以及速度Vi,Xi和Vi可通过式(13)进行初始化:
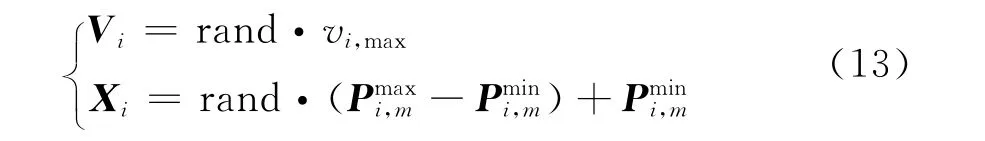
对于速度限值的设定可以取机组最大出力负荷值的一半,即有vi,max=-vi,min=0.5·pmaxm。
Step 2 按式(11)求初始种群的适应度值,将当前各粒子的最优位置存储在pbesti(t)中,将群体中最小适应度值所对应的pbesti(t)放在gbest(t)中。
Step 3 根据式(9)和式(10)更新粒子的速度和位置,对于越限的粒子将其限制在边界值上,按式(11)计算更新后粒子的适应度值。
Step 4 对更新后粒子的适应度值进行排序,选取群体20%较优的粒子进行混沌局部搜索[17],迭代次数达到max C或者混沌搜索后的适应值比先前适应值优,则退出混沌局部搜索,进入step 5。
Step 5 通过适应度值更新粒子pbesti与gbest(t)的值。
Step 6 按式(14)缩小搜索区域

其中0<r<1。
Step 7 在新的收缩区域内按式(13)随机生成80%的粒子,按式(11)计算粒子的适应度值。
Step 8 将经过step 4的粒子与step 7的粒子构成一个新的种群,取代原粒子群。
Step 9 若满足停止条件,即达到设定的粒子群迭代次数 max_gen,停止搜索,输出gbest(t)的值,否则返回Step3继续搜索。其中gbest(t)中的各个数值代表了消耗费用最低时的机组出力负荷值,即如式(15)所示:
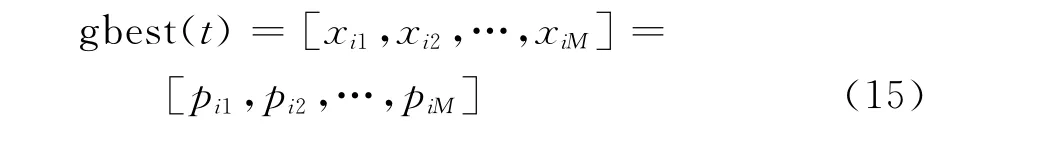
3 算例分析
为了验证本文ICPSO算法的有效、快速收敛以及结果的精确性,通过 MATLAB 7.8版本在E2140、主频1.60GHz、内存512MB的计算机上进行仿真实验,其中最大迭代次数max_gen=100,混沌局部搜索次数maxC=30,种群规模D=20,罚因子ξ=50。
算例1:采用文献[16]中的3机6母线系统为例,系统总负荷PD=850MW,考虑耗量曲线的阀点效应,忽略网损。表1给出了算例中发电机燃料耗量曲线特性参数以及有功功率限值。
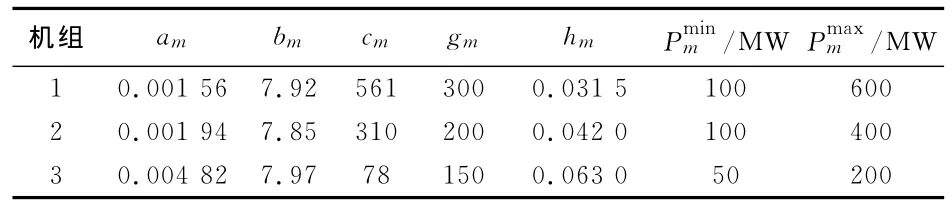
表1 机组特性参数Tab.1 Parameters of generating units
算例2:采用与算例1相同的系统,总负荷为500MW,计及阀点效应与网损,网损B系数如下:

对于文献[17]中提出的CPSO算法和本文ICPSO算法,分别对算例1和算例2进行独立仿真实验各50次,其平均适应值收敛效果如图1和图2所示。表2是算例1计及阀点效应,忽略网损的仿真计算结果。表3是算例2计及阀点效应和网损的仿真计算结果。表4和表5为各文献中采用不同算法在算例1和算例2中的仿真结果对比情况。

图1 算例1平均适应值收敛曲线图Fig.1 Average fitness convergence curves of case 1
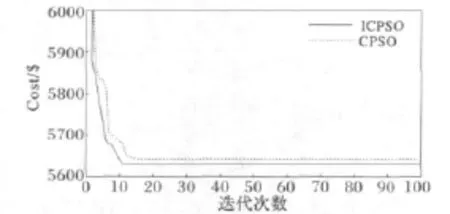
图2 算例2平均适应值收敛曲线图Fig.2 Average fitness convergence curves of case 2
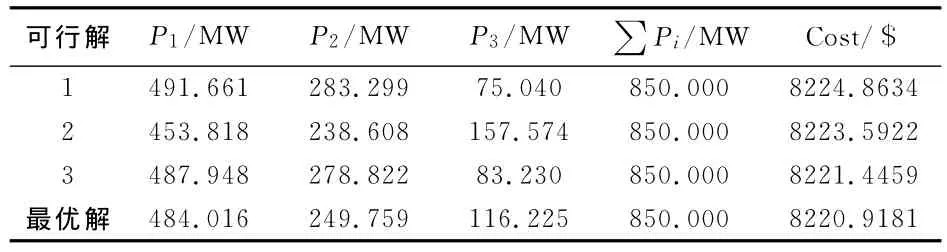
表2 算例1仿真结果Tab.2 Simulation results of case 1
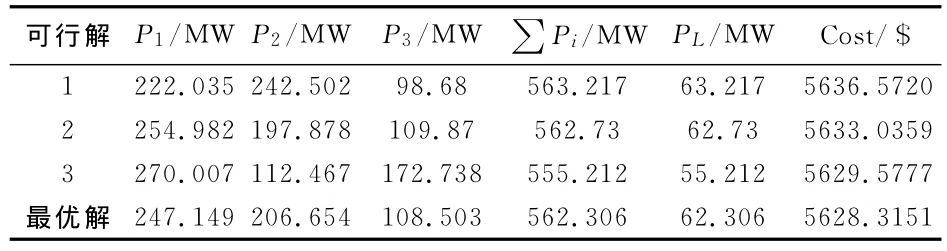
表3 算例2仿真结果Tab.3 Simulation results of case 2
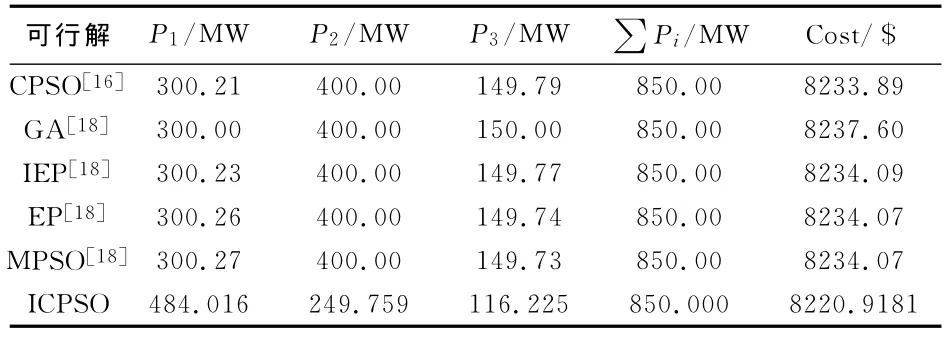
表4 不同算法在算例1中的仿真结果Tab.4 Simulation results of different algorithms in case 1

表5 不同算法在算例2中的仿真结果Tab.5 Simulation results of different algorithms in case 2
从图1和图2可以看出,文献[17]中的CPSO算法和本文ICPSO算法应用于不同算例中均体现了较快的收敛性能,在进化初期就可以初步达到精确的收敛效果,但相比之下,本文ICPSO算法在收敛性能和精确性方面略胜于文献[17]中的CPSO算法。表2和表3为ICPSO算法分别在算例1和算例2仿真结果中的几组可行解,通过表中数据显示,改进后的算法在结果上实现了更优。
通过表4仿真结果对比,本文提出的ICPSO算法所得出的总费用是最低的,从表5可看出,文献[9]和文献[10]中涉及到的算法,其网损与系统总负荷之和并不等于各机组的总出力值,换言之是以牺牲负荷平衡约束条件来获得最优费用,而本文ICPSO算法不仅总费用低,且能精确的满足负荷平衡约束条件。由此可得出,ICPSO算法有较好优越性。通过以上对照表明,本文所述ICPSO算法在快速性与精确性方面均达到令人满意的结果。
4 结语
本文对CPSO算法进行了改进,并在ELD问题上进行仿真实验,相比以往的CPSO算法以及其它智能算法取得了更优的效果,实现了快速寻优与结果的精确性。由于混沌粒子群算法属于随机性算法,相比确定性算法在结果上存在随机性,加之ELD问题是多维的且含较多复杂约束条件,因此在后面的研究工作中,需要考虑算法在多机组运行、机组启停、机组的爬坡限制以及环境负荷调度多目标优化问题等方面结果的精确性以及快速收敛性。ICPSO算法在实际系统中的成功应用,将会为相关行业带来一定的经济效益。
[1] Walters D C,Sheble G B.Genetic algorithm solution of economic dispatch with valve point loading[J].IEEE Trans on Power Systems,1993,8(3):1325-1332.
[2] 侯云鹤,熊信艮,吴耀武,等(Hou Yunhe,Xiong Xinyin,Wu Yaowu,et al).基于广义蚁群算法的电力系统经济负荷分配(Economic dispatch of power systems based on generalized ant colony optimization method)[J].中国电机工程学报(Proceedings of the CSEE),2003,23(3):59-64.
[3] Jabr R A,Coonick A H,Cory B J.A homogeneous linear programming algorithm for the security constrained economic dispatch problem[J].IEEE Trans on Power Systems,2000,15(3):930-936.
[4] 马玲,王爽心,刘如九,等(Ma Ling,Wang Shuangxin,Liu Rujiu,et al).基于改进动态规划法的火电厂负荷经济调度(Load economic dispatching of thermal power station based on improved dynamic programming method)[J].北京交通大学学报(Journal of Beijing Jiaotong University),2005,29(4):100-103.
[5] Shiina Takayuki,Watanabe Isamu.Lagrangian relaxation method for price-based unit commitment problem[J].Engineering Optimization,2004,36(6):705-719.
[6] 何大阔,王福利,毛志忠,等(He Dakuo,Wang Fuli,Mao Zhizhong,et al).遗传算法在电力系统经济负荷分配中的应用(Application of genetic algorithm on economic dispatch of power systems)[J].系统仿真学报(Journal of System Simulation),2007,19(4):890-892,900.
[7] 范宏,韦化(Fan Hong,Wei Hua).改进遗传算法及其在机组优化组合中的应用(Improved genetic algo-rithm and its application in unit commitment optimization)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2004,16(4):46-49,63.
[8] 毛 亚 林,张 国 忠,朱 斌,等 (Mao Yalin,Zhang Guozhong,Zhu Bin,et al).基于混沌模拟退火神经网络模型的电力系统经济负荷分配(Economic load dispatch of power systems based on chaotic simulated annealing neural network model)[J].中国电机工程学报(Proceedings of the CSEE),2005,25(3):65-70.
[9] 唐巍,李殿璞(Tang Wei,Li Dianpu).电力系统经济负荷分配的混沌优化方法(Chaotic optimization for economic dispatch of power systems)[J].中国电机工程学报(Proceedings of the CSEE),2000,20(10):36-40.
[10] 修春波,陆丽芬(Xiu Chunbo,Lu Lifen).改进的混沌优化算法及其在电力系统负荷分配中的应用研究(Chaos optimization algorithm and its application in economic load dispatch on power system)[J].电力系统保护与控制(Power System Protection and Control),2010,38(21):109-117.
[11] 张雪雯,李艳君(Zhang Xuewen,Li Yanjun).基于自调节粒子群算法的电力系统经济负荷分配(Self-adjusted particle swarm optimization algorithm based economic load dispatch of power system)[J].电网技术(Power System Technology),2006,30(18):8-13.
[12] 赵波,曹一家(Zhao Bo,Cao Yijia).电力系统机组组合问题的改进粒子群优化算法(An improved particle swarm optimization algorithm for power system unit commitment)[J].电网技术(Power System Technology),2004,28(21):6-10.
[13] 唐英干,崔玉红,乔雷杰,等(Tang Yinggan,Cui Yuhong,Qiao Leijie,et al).一种新算法在经济负荷分配中的应用(Application of simplex search method and particle swarm optimization in economic dispatch)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2009,21(1):20-26.
[14] 蒋秀洁,吴永华,杨敏(Jiang Xiujie,Wu Yonghua,Yang Min).基于PSO-GA算法的电力系统机组组合研究(PSO-GA algorithms for unit commitment of power system)[J].继电器(Relay),2006,34(5):34-38.
[15] 陈如清,俞金寿(Chen Ruqing,Yu Jinshou).混沌粒子群混合优化算法的研究与应用(Study and application of chaos-particle swarm optimization-based hybrid optimization algorithm)[J].系 统 仿 真 学 报(Journal of System Simulation),2008,20(3):685-688.
[16] 蒙文川,邱家驹(Meng Wenchuan,Qiu Jiaju).电力系统经济负荷分配的混沌粒子群优化算法(Chaotic particle swarm optimization algorithm for economic load dispatch of power system)[J].电力系统及其自动化学报(Proceedings of the CSU-EPSA),2007,19(2):114-119.
[17]Bo Liu,Ling Wang,Yi-Hui Jin,et al.Improved particle swarm optimization combined with chaos[J].Chaos,Solitons and Fractals,2005,25(5):1261-1271.
[18]Park J B,Lee K S,Shin J R,et al.A particle swarm optimization for economic dispatch with nonsmooth cost functions[J].IEEE Trans on Power Systems,2005,20(1):34-42.
