变速恒频双馈风电机组的动态等值方法

刘力卿，余 洋，王 哲，王 磊

（华北电力大学电气与电子工程学院，保定071003）

随着风电技术的快速发展，风力发电在电力系统中的比重持续增加，对电网的影响也越来越大［1］。为研究大型风电场接入对电网的影响，风电机组的准确建模成为关键［2］。

目前，变速恒频双馈风电机组以其自身的优势成为风电市场上的主流机型。对于大型并网运行的变速双馈风电机组风电场，如果对风电场内每台双馈风力发电机及其控制系统进行单独建模，不仅会增加电力系统模型的规模，而且还会带来许多严重问题［3］，如：模型的有效性如何验证，数据如何修正等，同时也将大大增加仿真计算的时间，甚至无法进行仿真。针对这一问题，本文在建立了单台双馈风力发电机的动态数学模型的基础上，提出一种变速恒频双馈风电机组的动态等值方法，建立了风电场内所有风力发电机组的动态等值模型，该等值模型包括：风力机模型、发电机模型以及控制系统模型，利用PSCAD／EMTDC软件平台进行仿真，仿真结果表明，该方法是可行的，而且具有较高的仿真精度。

1 双馈风力发电机动态数学模型

1.1 风力机数学模型

风力机的空气动力学模型为

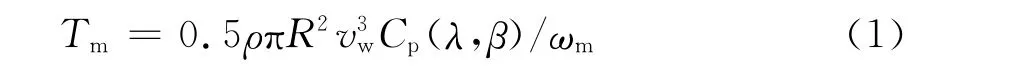
式中：Tm为风力机的机械转矩；ρ为空气密度；R为风机叶轮半径；Vw为风速；ωm为风力机的转速；λ为叶尖速比；β为桨距角；Cp为叶片的风能利用系数，Cp是λ与β的函数。

1.2 双馈发电机数学模型

规定定子侧以发电机惯例为正方向，转子侧以电动机惯例为正方向，列出双馈发电机的动态数学模型如下。

电压方程：

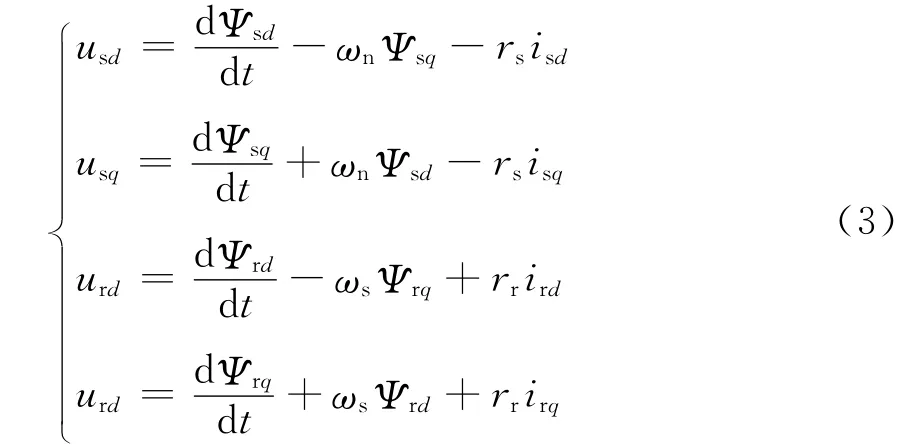
磁链方程：

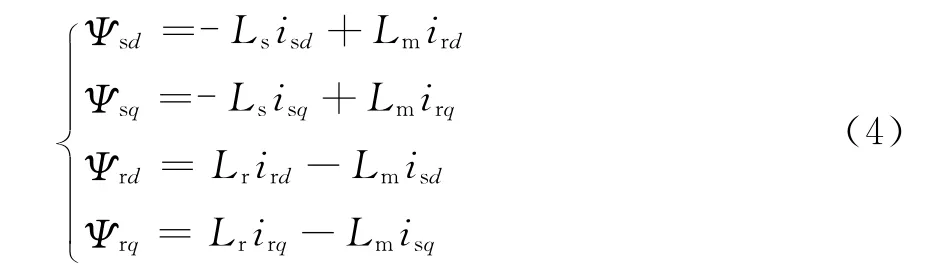
式中：下标s、r分别代表定子和转子；rs、rr分别为定子和转子的电阻；Ls、Lr分别为定子和转子电感；Lm为定子和转子互感；ωs＝ωn－ωm，其中ωn为同步转速。

发电机转子运动方程为

式中：J为发电机转子转动惯量；Tm为风力机的机械转矩；Te为发电机电磁转矩；ω为发电机转速；p为发电机极对数。

1.3 双馈风力发电机控制系统数学模型

双脉宽调制 PWM（pulse－width modulation）变频器是由两个背靠背的三相电压源型整流／逆变器构成，连接于发电机定子和转子之间，使发电机的定子和转子之间能够进行能量双向流动。利用矢量控制技术进行控制，能够对风力发电机的有功功率和无功功率进行解耦控制，实现最大的风能追踪。

电网侧变频器采用电网电压定向控制技术，控制模型为

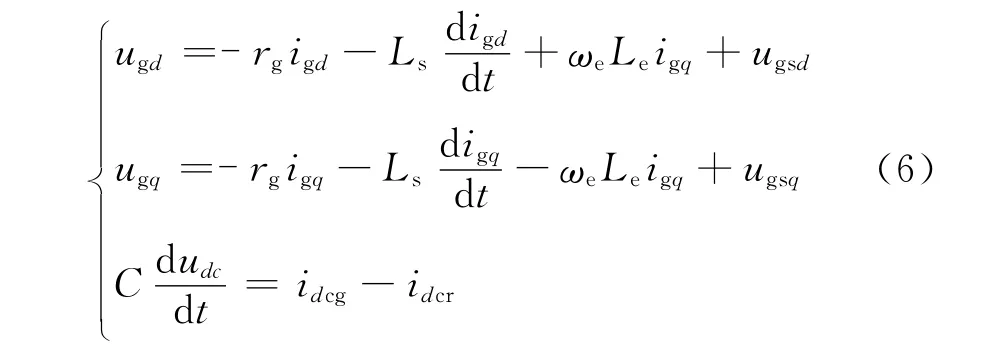
式中：ugd、ugq为电网电压的d－q 轴分量；ugsd、ugsq、igd、igq分别为电网侧变频器的电压、电流的d－q轴分量。

转子侧变频器采用定子磁链定向控制技术，控制模型为

2 变速恒频双馈机组动态等值模型

现实中，风电场内所有风电机组大都并联在同一母线上，基于上述情况，本文假设所有风机均并联于同一母线，并且运行状况相同，不考虑风电场并网运行时双馈发电机组内部的功率损耗，通过应用加权平均法对风力发电机组进行等值，然后利用单纯形法对比例积分控制器PI（proportion－integral）的控制参数进行寻优，得到精确的等值模型［4］。

2.1 等值风力机模型

等值风力机的容量等于各台风力机容量之和，输出机械转矩等于各台风机输出机械转矩之和，即

式中：Tim（i＝1，…，n）为每台风力机的机械转矩；Teqm为等值风力机的机械转矩；n为风电场中风电机组的数量总数。

2.2 等值发电机模型

等值发电机的容量等于各台发电机容量之和，即

式中：Si（i＝1，…，n）为每台发电机的额定容量；Seq为等值发电机的额定容量，n为风电场中风电机组的数量总数。

等值发电机所有阻抗参数均可通过容量加权平均法求得，公式为

式中：Z为待求等值发电机的等值阻抗参数；Zi（i＝1，…，n）为每台发电机的阻抗参数。

等值发电机的转子转动惯量等于每台电机转子转动惯量之和，并由式（11）和（12）可求出等值发电机的等值转子惯性时间常数。

式中：Jeq为等值转子转动惯量；Ji（i＝1，…，n）为每台机转子转动惯量；Teq为等值转子惯性时间常数。

2.3 控制系统等值模型

等值风力发电机的变频器连接于等值发电机的定子和转子之间，其变频器容量相当于各台机变频器容量之和，定子与转子之间的流动能量等于所有单机变频器流动能量之和。等值风力发电机变频器分别与转子和定子相连的阻抗参数等值方法与2.2节中等值发电机阻抗参数等值方法相同，此处不再赘述。

等值风力发电机变频器的直流环节电压与单台风力发电机变频器直流环节电压等级相同，直流环节电容等于各台机变频器直流电容之和，即

式中：Ceq为等值风力发电机变频器直流环节的等值电容；Ci（i＝1，…，n）为每台机变频器直流环节电容。

等值风力发电机的控制系统模型与单台机控制系统模型完全相同，将单机控制系统的PI参数值作为等值机控制系统控制参数的初始值，利用单纯形法［5］对其进行优化，使控制效果达到最佳。

2.4 参数优化

非线性单纯形算法是广泛应用的直接搜索方法，是最优化技术无约束极值直接法中比较有效的方法之一，是基于几何形状考虑的启发式优化算法。本文中需要进行优化的控制系统PI控制器参数［6］主要包括：转速控制模块PI参数K1、T1，定子无功输出控制模块PI参数K2、T2，直流环节电压控制模块PI参数K3、T3，变频器无功输出控制模块PI参数K4、T4，变桨距功率控制模块PI参数K5、T5。

选择时间乘以误差绝对值积分的性能指标作为变频器控制系统参数优化的目标函数。目标函数表示如下：

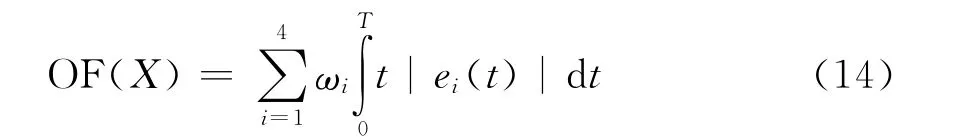
式中：ei（t）为系统目标设定值和目标实际值之间的误差，e1（t）＝ωr（t）－ωrref，e2（t）＝Q（t）－Qref，e3（t）＝Uc（t）－Uref，e4（t）＝igq（t）－igqref，e5（t）＝Ps（t）－Psref；T为系统运行时间；X为控制系统参数，ωi为 权 重，X＝ （K1，T1，K2，T2，K3，T3，K4，T4，K5，T5）。

以单台机模型的控制参数为初始值，优化前后各PI控制器的参数对比如表1所示。

表1 初始、优化后控制参数对比Tab.1 Comparison of the initial value and optimized control parameters

3 仿真算例

为验证本文所提等值方法的可行性，以对含25台相同型号的额定容量为2MW的变速双馈风电机组的风电场等值为例，在PSCAD／EMTDC软件平台中分别搭建25台机的全仿真模型和等值模型，比较两模型在风速扰动和故障扰动时的运行特性，单台风机与等值后风机的参数对比如表2所示。

风电场中每台风力发电机经过0.69／35kV升压变压器并联接在同一母线L1上，然后通过双回线和35／110kV升压变电站T2连接到电网，并在变电站T2装设无功补偿设备以稳定风电场接入电压，风电场接线如图1所示。

表2 单台机、等值机参数对比Tab.2 Parameters of the single and equivalent model

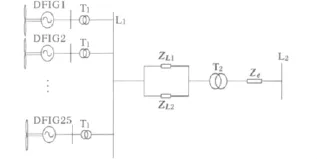
图1 风电场接线图Fig.1 Complete wind farm

风力发电机组等值前后

仿真1：在平均风速8m／s的基础上，加入阵风和随机风的作用，对风电场全仿真模型和等值模型进行仿真，仿真结果如图2所示。

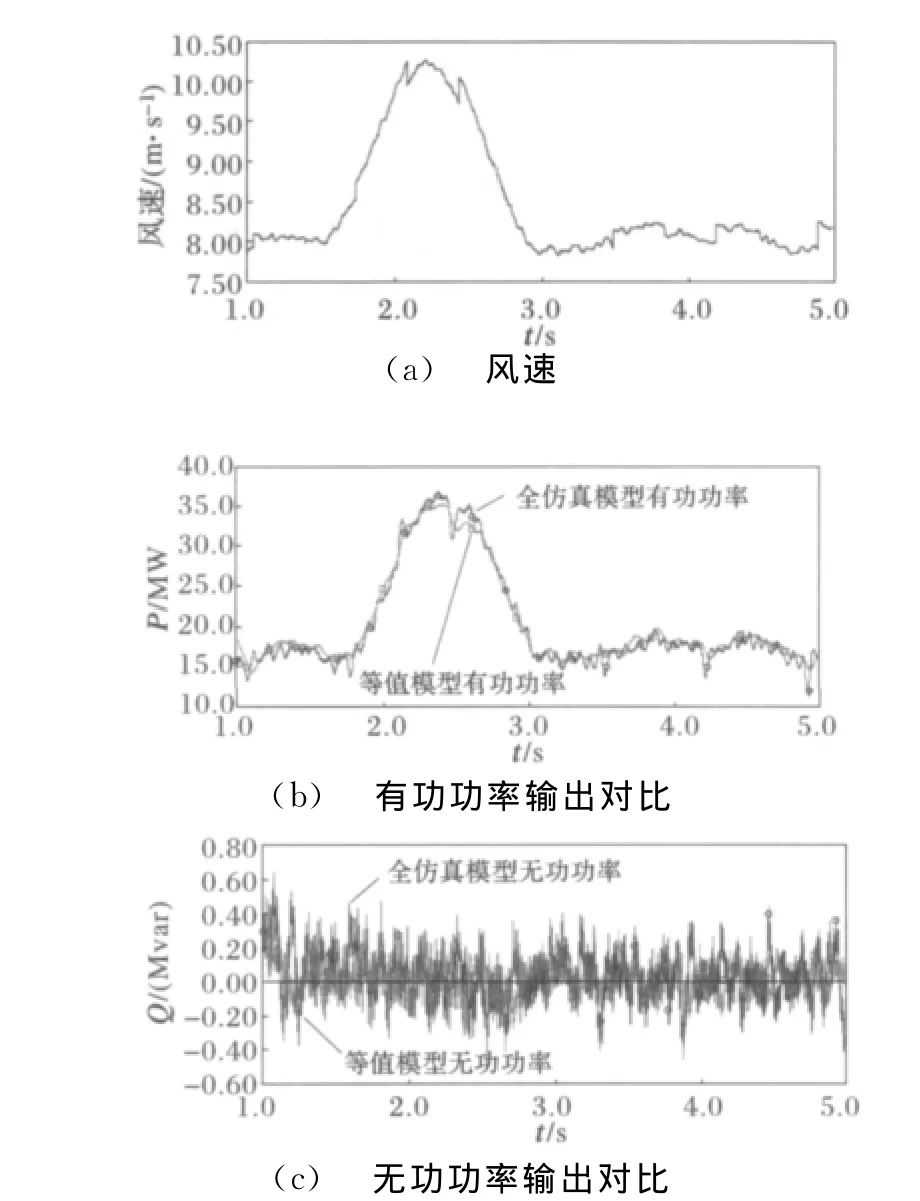
图2 风电场全仿真模型与等值模型控制特性对比Fig.2 Comparison of the dynamic simulation results of complete and equivalent wind farm during normal operation

仿真2：风速为10m／s并保持不变，风电机组运行状态不变。在3s时母线L2处发生三相短路故障，故障持续0.5s，风电场全仿真模型和等值仿真模型发生以上故障时的仿真结果见图3。

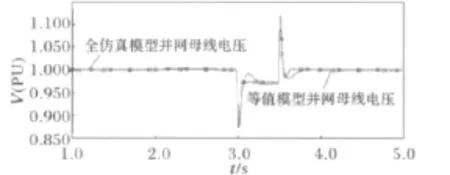
图3 风电场全仿真模型与等值模型并网处母线电压对比Fig.3 Comparison of the bus voltage at PCC of complete and equivalent wind farm

通过以上仿真可见，风力发电机组的等值模型与全仿真模型在风速扰动和故障扰动时，动态特性基本相同，本文所提等值方法可行。

4 结语

本文提出一种变速恒频双馈风电机组动态等值方法，首先建立了单台变速恒频双馈风力发电机的动态数学模型，然后在此基础上对风电场内所有双馈风力发电机组进行等值，并通过仿真验证了该等值方法是可行的，为研究风电场对系统的影响提供了良好的基础。

［1］ Chen Z.Issues of connecting wind farms into power systems［C］∥IEEE／PES Transmission and Distribution Conference and Exhibition，Dalian，China：2005.

［2］ 迟永宁（Chi Yongning）.大型风电场接入电网的稳定性问题研究（Studies on the Stability Issues about Large Seale Wind Farm Grid Integration）［D］.北京：中国电力科学研究院 （Beijing：China Electric Power Research Institute），2006.

［3］ 孙蕾（Sun Lei）.变速恒频风力发电机组建模与控制策略研究（Study on Model Establishment and Control Strategy of VSCF Wind Power Generation System）［D］.保定：华北电力大学电力工程系（Bao ding：Department of Electrical Engineering of North China E－lectric Power University），2010.

［4］ 李环平，杨金明（Li Huanping，Yang Jinming）.基于PSCAD＿EMTDC的大型并网风电场建模与仿真（Model and simulation of large grid connected wind farm based on PSCAD＿EMTDC）［J］.电力系统保护与 控 制 （Power System Protection and Control），2009，37（21）：62－66.

［5］ 张开明（Zhang Kaiming）.基于 PSCAD／EMTDC变速恒频风电机组控制系统仿真（Simulation of the variable－speed constant－frequency wind turbine control system based on PSCAD／EMTDC）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2008，20（3）：70－76.

［6］ 杨伟，赵广，蔡开龙（Yang Wei，Zhao Guang，Cai Kailong）.基于单纯形法的PID整定及其在气动压力伺服系统中的应用（PID parameters tuning based on simplex algorithm and its application in pneumatic pressure servo system）［J］.液压与气动（Chinese Hydraulics ＆ Pneumatics），2007，31（11）：53－55.