感应电机低速控制方法

王 涛，徐英雷

（西南交通大学电气工程学院，成都610031）

感应电机由于其变量非线性耦合，转子电量难以测量，同时电机参数时变性导致感应电机高精度交流调速控制相当复杂［1］，尤其是在电机低速运行时，条件更为苛刻。为了获得优良的调速动静态性能，控制问题一直是研究的热点。速度控制是感应电机驱动系统的核心，速度测量需要在电机轴上安装速度传感器，可实现对速度控制和转矩控制。然而，速度估计优越于速度测量，间接磁场定向无速度传感器技术广泛应用在感应电机驱动上，虽然无速度传感器技术在电机高速具有很好的性能，但是它在低速时性能变得很差。然而，带有磁通观测器的直接磁场定向控制方法，这是因为磁通估计器在低速时，此时磁通估计的极点，在其S域的原点附近。同时，磁通观测器使用纯积分器，由于积分器漂移和初始条件，导致对电压传感器和电机定子电阻变化非常敏感，不能很好地应用于实际。并且，感应电机无速度传感器矢量控制中，速度辨识系统在零频或极低速时会不稳定，是由于其反电动式很低，定子电阻变化或者测量误差，低速运行相当苛刻；同时，由于缺失了电机转子侧的信息，电机转子参数不匹配引起的扰动导致的结果。零频时，此时信号激励为零，电机转子速度与转子磁通不能使用传统的观测器，因为此时只存在单一输入，在理论上不能解决零速问题［2，3］。

为了在零频时不用速度测量，而控制感应电机，则需消除输入的单一性。一些速度估计算法，比如高频电压信号注入或者正弦PWM电压波，来估计零频时的转子速度，这些方法将电压作为通用输入，是有效的。许多的速度估计方法应用于感应电机矢量控制，其中MARS由于其简单直接的稳定算法，成为了流行的方法。比如磁链、反电动和无功都是基于MRAS函数的方法。

本文在传统观测器中引入V信号，解决低速激励信号不足，使得系统稳定收敛，且能很好地辨识电机转子速度。

1 感应电机数学模型

根据电机学理论，感应电机在两相静止α－β坐标系下，状态方程为［5］

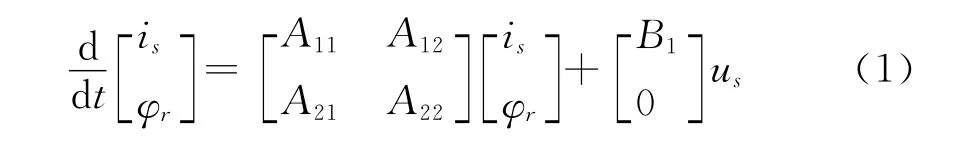
其中：

式中：R1、R2为定转子电阻；L1、L2为定转子自感；Lm为互感；δ为漏磁系数；δ＝1－／L1L2；τr为时间常数；ωr为电机角速度。

由式（1）可以得

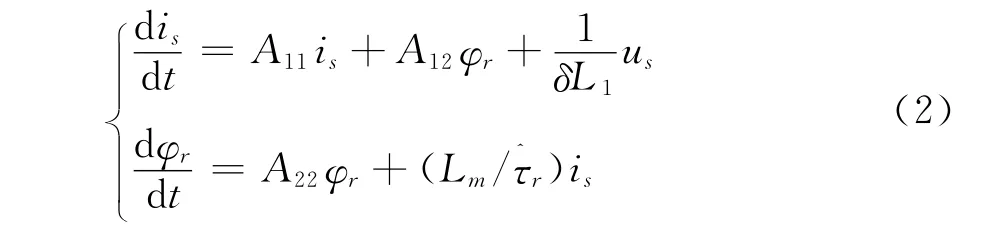
2 观测器的设计

定义上标符号“＾”为观测值，传统降阶观测器方程为

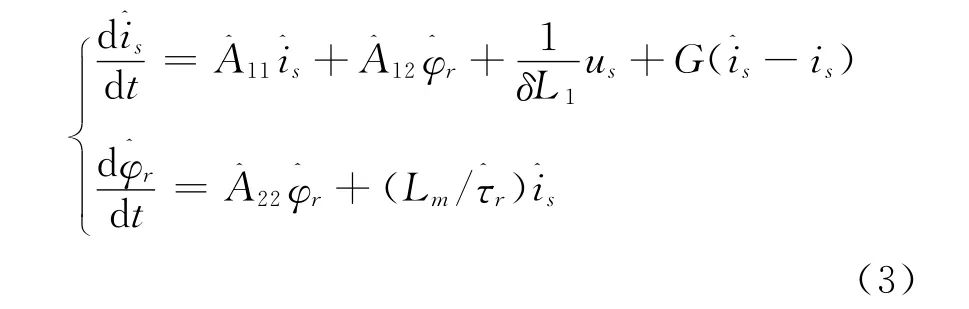
其中，G为观测器增益矩阵，即

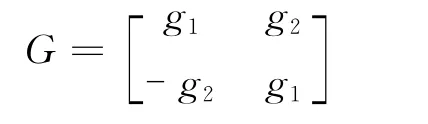
使误差响应的快速性与外界干扰及测量噪声达到一种折中，配置观测器增益矩阵G的极点，使观测器的特征值为负，这样观测状态量会收敛于待观测系统的状态值。观测器的特征值某种程度上更负于待观测系统的特征值，从而比其它系统收敛的速度更快。基于上述考虑，选择如下：

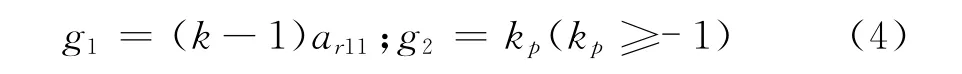
因为在低速和零频时，此时磁通估计的极点，其在S域的原点附近，导致对电压传感器和电机定子电阻变化非常敏感。为此在上式观测器中引入V信号，解决低速激励信号和系统稳定收敛、辨识转子速度。其中：V ＝ ［v1v2］′，v1和v2是要设计的感应电机输入量，即为添加的激励信号。

由此观测器的结构［6］，用下式表示：

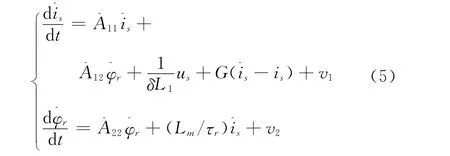
观测器结构如图1所示。

图1 观测器结构Fig.1 Structure of observer

由式（5）减去式（2），有：

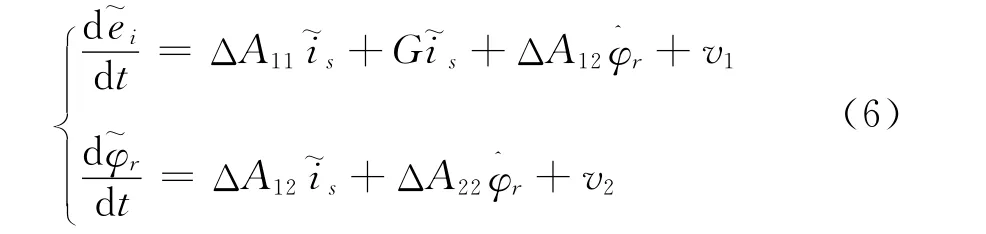
设定Lyapunov函数为

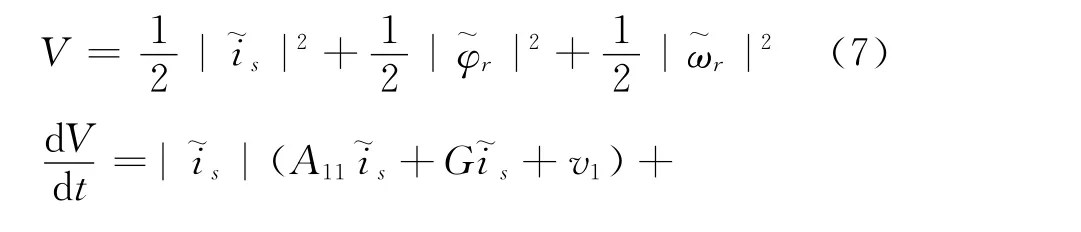
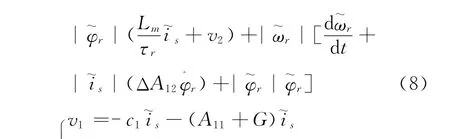
综上有

根据Lyapunov稳定性定理，由式（9）可以看出观测电流值会趋近实际电流值；转子转速跟随实际值，可以在线辨识转子速度；同时转子磁链渐近跟踪参考磁链，能够保证设计方法的性能稳定性和快速收敛性。

3 仿真算例结果

对一台鼠笼式感应电机，其参数：额定功率PN＝35kW，额定电压UN＝380V，额定频率fN＝50Hz，定子电阻Rs＝0.4Ω，转子电阻Rr＝0.5 Ω，Ls＝0.087H，互感Lm＝0.085H，Lr＝0.088 H，极对数np＝2，J ＝0.0876kg·m2，利用Matlab／simulink进行仿真［7］。仿真结果如图2和图3所示。

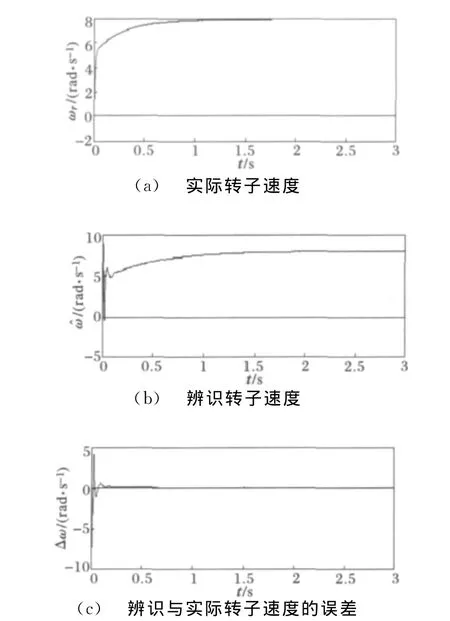
图2 低速段的速度估计Fig.2 Speed estimation at very low－speed subsection

设定感应电机负载转矩为一定值，其大小为15N·m。参考模型是有速度传感器的闭环系统，转子速度自适应系统为无速度传感器系统，其转速跟踪参考模型输出值。仿真时电机的实际转速指参考模型的输出值。

设定转子转速参考值ω＊r＝8rad／s，电机实际转速如仿真图2（a）所示，辨识转子转速如仿真图2（b）所示，电机转速与辨识转速的误差，如仿真图2（c）所示，实际转速很快能够收敛于转速参考值，感应电机启动时，辨识转速与实际转速之间有一个较大的波动误差，产生原因为参考模型系统的转子转速值，在启动瞬间有突变，导致自适应模型系统的转子速度有剧烈的波动，但是0.2s后，辨识转速能很快的趋近实际转速。

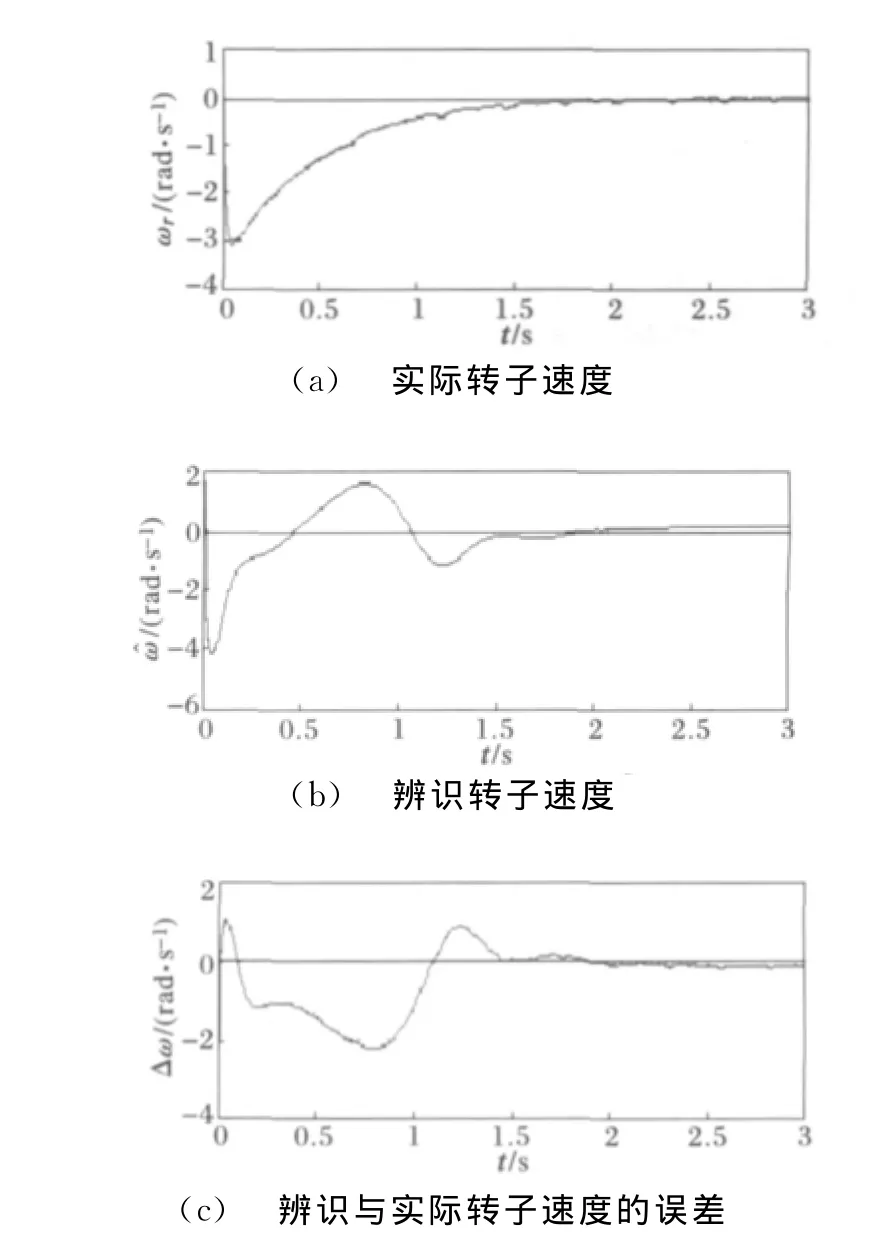
图3 零频时的速度估计Fig.3 Speed estimation at zero－frequency

仿真结果显示感应电机在低速或零速时转子转速能观测，系统有良好的调速性能和稳定性能。

4 结语

基于模型参考自适应方法，在其观测器中引入V信号，采用非线性Lyapunov理论分析和证明了电机的电磁子系统的收敛性，给出交流调速系统的一种具有鲁棒性的自适应控制律，解决低速激励信号不足，达到系统稳定收敛，辨识转子速度，克服了一般矢量控制中在低速段时磁链观测不准的缺点。理论证明该控制方案保证转子磁链、转速都能全局稳定跟踪，同时仿真结果表明系统具有良好的动静态性能，控制系统结构简明，易于实现。

［1］ 李永东.交流电机数字控制系统［M］.北京：机械工业出版社，2002.

［2］ Wang Huangang，Zhang Xiaoping，Xu Wenli，et al.The speed－sensorless control of induction motors at zero frequency［C］∥Fifth International Conference on Electrical Machines and Systems，Shenyang，China：2001.

［3］ Yamaguchi N，Hasegawa M，Doki S，et al.A stabilization method for speed sensorless vector controlled induction motors at zero frequency operating condition with multirate adaptive observer［C］∥30th An－nual Conference of IEEE Industrial Electronics Society，Busan，South Korea：2004.

［4］ Kubota H，Matsuse K，Nakano T.DSP－based speed adaptive flux observer of induction motor［J］.IEEE Trans on Industry Applications，1993，29（2）：344－348.

［5］ Madadi Kojabadi H，Chang L.Model reference adaptive system pseudoreduced－order flux observer for very low speed and zero speed estimation in sensorless induction motor drives［C］∥33rd Annual IEEE Power Electronics Specialists Conference，Cairns，Australia：2002.

［6］ 肖建.现代控制系统综合与设计［M］.北京：中国铁道出版社，2000.

［7］ 顾德英，季正东，张平（Gu Deying，Ji Zhengdong，Zhang Ping）.基于SIMULINK的异步电机的建模与仿真（Modeling and simulation of asynchronous motors based on SIMULINK）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2003，15（2）：71－73.