风险理论思想下的输电线路脆弱性综合分析

张晓辉，李 颖，卢志刚

（燕山大学电力电子节能与传动控制河北省重点实验室，秦皇岛066004）

电网规模的不断扩大化及系统元件的不断复杂化是当前电力系统发展的主要特点。仅按现有的稳定性、可靠性准则来保证电力系统的安全、稳定运行是不够的，人们需要提前预知电网中存在的潜在危险，找出电网中存在的安全隐患，并采取恰当措施对电网的脆弱环节进行修复，使可能发生的故障范围尽量缩小、故障强度尽量降低，从而提高电力系统保持其安全和稳定运行的能力，由此便引入了脆弱性理论。

近年来，国内外的学者对电力系统脆弱性的研究主要有确定性评估和非确定性评估两种方法。确定性评估主要包括灵敏度法、能量裕度法、潮流法、直接法等［1］。其中能量函数和裕度指标作为电网脆弱性评估指标有着非常广泛的应用［2～4］，在实际应用中，根据分析侧重点不同，要选择相应的脆弱性指标进行衡量。非确定性方法主要是针对电网故障的不确定性进行的研究，其主要方法包括概率和风险理论、复杂网络理论、人工智能等。文献［5～7］将风险理论与人工智能相结合的方法运用到电力系统脆弱性评估中，是典型的非确定性方法的组合应用。文献［8］建立多Agent分层控制系统对电力系统脆弱性进行评估，并为系统提供在随机环境中的自我适应和自我恢复能力。文献［9，10］从电网拓扑结构出发，强调电网整体构架对故障传播的影响。文献［11，12］采用同时考虑状态量和拓扑参数的评估方法，但都没考虑故障发生的概率，假设某种故障的后果特别严重但是发生概率特别小的话，这条线路的脆弱性也不是很高。本文运用风险理论的方法实现了电力系统线路脆弱性的评估。该方法从线路故障发生的概率和造成的影响入手对输电线路脆弱性进行评估。首先计算各条传输线路的故障概率；然后从网络结构、运行状态两方面对故障造成的后果进行研究，最后运用风险理论的方法对电网输电线路的脆弱性进行综合评估。

1 电力系统脆弱性分析

电力系统脆弱性评估是在电力系统安全性［13，14］评估和经济性评估基础上提出的，是在电力系统安全稳定运行的状态下，对电力系统中潜在故障的一种预测和分析。具体来说，电力系统脆弱性描述的是电力系统及其构成元件在一些无法预知的扰动或故障发生的时候，受到影响和破坏的程度，以及抗击干扰和恢复正常运行的能力。

电力网络的拓扑参数：

1）网络冗余度［9］网络冗余度定义为移除有线路直接相连的两个节点间的线路之后连接这两个节点的线路条数，如果两点间没有其他路径相连，则认为两个节点之间网络冗余度为无穷大。

2）线路介数［9］线路介数指线路被网络中所有发电机节点与负荷节点间最短路径经过的次数。

基本模型的建立：

1）只考虑高压输电网，不考虑配电网和发电厂、变电站的主接线；

2）网络中所有节点分为三个集合，发电机节点集合、负荷节点集合、变电站节点集合，不考虑大地节点；

3）所有边均为无向有权边，将线路的电抗值作为线路的权重，不考虑输电线的各种特性参数和电压等级的不同；

4）合并同杆并架输电线，不计并联电容支路（消除自环和多重边），使模型成为简单图；

5）电网就等效为一个具有N个节点K条边的有权无向的稀疏连通图；

6）故障模式：由于单一线路故障跳闸退出运行在电力系统故障中比较普遍，因此本文以单一线路故障作为电网基本故障模式。

2 基于风险理论的输电线路脆弱性分析

“风险”一词用来表达可能发生的不利事件或各种灾害，风险与自然状态的不确定性、人的主观行为及两者结合所蕴含的潜在后果有关。所谓风险理论就是考虑系统中不确定因素的理论，风险评估是指采用一系列逻辑步骤检测出系统中潜在的危害，从而采用恰当措施降低系统潜在危险的过程。

本文将电力系统定义为一个脆弱的系统，并从输电线路故障的发生概率和造成的影响两方面入手对电力系统输电线路的脆弱性进行评估。电力系统线路脆弱性评估需要定量把握线路故障发生的可能性和严重性两个指标。

2.1 概率评估模型

线路故障概率表示为线路在单位时间内发生故障的次数，该指标表征了线路发生故障可能性的大小。从事故统计数据可以得出电力系统发生各种线路故障的概率基本符合泊松分布［1］：

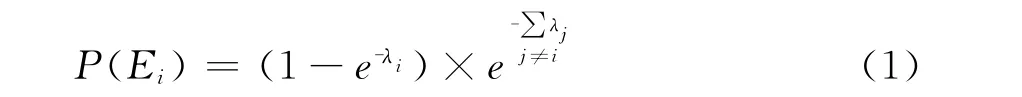
式中：λi是可能事故Ei的发生率。

2.2 输电线路脆弱性指标计算

1）结构脆弱性指标

网络冗余度反映节点间备用最短线路的长度。本文电力系统中所有线路均简化为无向有权边，线路的权重为线路的电抗值，并根据网络任意两点之间的最短电气路径为两点之间所有路径中沿线线路权重和最小的路径，定义线路的网络加权冗余度R为：移除有线路直接相连的两个节点间的线路之后连接这两个节点的最短电气路径与原直接相连路径的比值，如果两点间没有其他路径相连，则认为两个节点之间加权网络冗余度R为无穷大。

带权重线路介数［15］：若线路（m，n）被发电机i与负荷j间最短电气路径经过，该线路需承担发电机i带来的负载Wi。定义线路（m，n）的带权重线路介数为

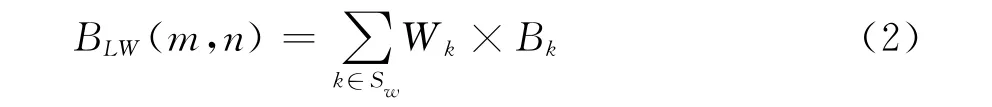
式中：Bk为第k条线路的介数，Sw为经过（m，n）的最短路径的发电机序号集合。

本文定义利用节点负荷经济因子修正的加权线路介数为经济因子加权介数，进一步细化了各节点结构脆弱度的合理性：

式中：αk为各个负载的经济因子。

结构脆弱性是在电力系统正常运行情况下，保持其拓扑结构完整性的能力。对一给定输电网来说，结构脆弱性就是对电网固有脆弱强度的反应。本文中结构脆弱性引入网络加权冗余度R来衡量，考虑到介数的大小反映线路的访问量和通行能力以及在电网中的活跃程度，本文引入加权介数并进行改进，将经济因子加权介数BLM作为各条线路结构脆弱性的权值。结构脆弱性指标的计算方法为：首先计算各条线路的加权网络冗余值Rl（1≤l≤k），然后计算各条线路的经济因子加权介数BLM，各条线路的结构脆弱度指标为

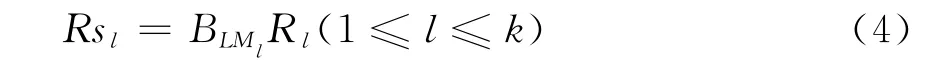
2）状态脆弱性指标

状态脆弱性是指系统遭受扰动或故障后，元件状态变量偏离正常状态或距离临界值的程度，传统的状态脆弱性评估基本都只是单独通过比较各节点电压裕度来确定元件的脆弱性排序。节点的电压裕度是自身稳定状态与临界状态电压的差值，同一节点在不同系统运行环境下电压裕度值的比较以及相同运行环境下单独比较不同节点的电压裕度值对分析系统的安全性还存在一定程度的不足。基于上述思想，本文综合考虑输电网各节点电压和各输电线路传输功率的整体裕度。

状态脆弱性指标的计算方法如下。

结点电压和支路功率的绝对临界裕度为

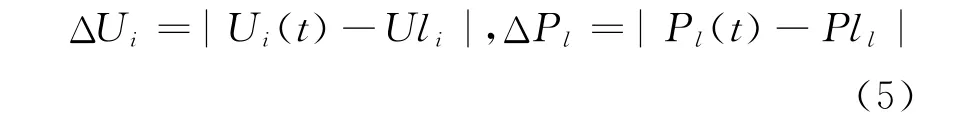
结点电压和支路功率的相对临界裕度为

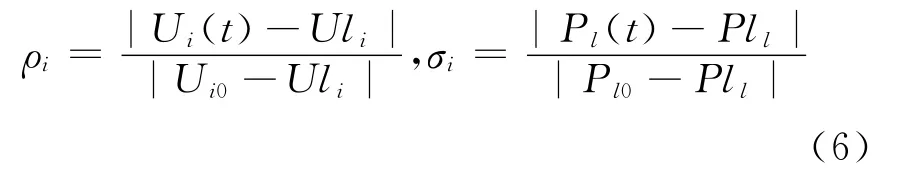
式中：Ui（t）和Pl（t）为电网节点电压和支路功率当前值；Uli和Pll为电网节点电压值和支路功率值的临界值；Ui0和Pl0为电网节点电压和支路功率的初始安全裕度；Pll为系统正常运行时线路的传输功率。

第l条线路（1≤l≤k）的状态脆弱性指标为第l条线路故障后电网中节点电压整体相对裕度和支路整体传输功率相对裕度的乘积的倒数：

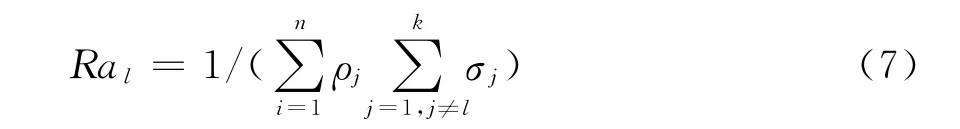
从数学表达式可以看出ΔU和ΔP在“程度”方面反映了电网发生扰动或故障时，电网节点电压和支路功率的变化量，但是同样大小的变化量在裕度不同的情况下脆弱程度是明显不同的，ρ和σ在ΔU和ΔP的基础上补充了这点。

传统脆弱性评估一般通过计算节点电压裕度评估系统节点的脆弱性，其中关键步骤是对临界电压值的求取。计算临界电压值［16～18］的速度和精度将对电压裕度的求取速度和精度具有决定性影响，因此计算临界电压需寻求相对快速和准确的算法。传统的PNFA算法较之牛顿法等，计算速度有很大提高，文献［19］在传统PNFA算法展开式的基础上引入优化乘子 ，提高了计算速度和精度。本文应用文献［19］的算法对临界电压值进行求取。

3）综合脆弱性指标

按照风险理论原理从故障发生概率和造成的影响入手，并将线路故障产生的后果定义为结构脆弱性指标和状态脆弱性指标的加权和，权值各为0.5。第l条线路（1≤l≤k）的综合脆弱性指标为

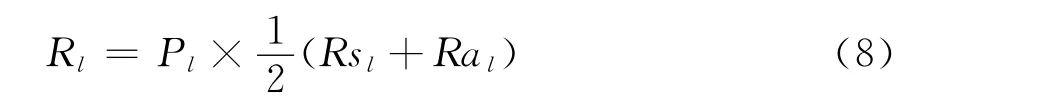
式中：R为第l线路的综合脆弱性指标；Pl为第l线路的故障发生概率；Rsl为第l线路的结构脆弱性指标；Ral为第l线路的状态脆弱性指标。

3 算例分析

本文采用IEEE14节点作为测试系统，如图1。

1）分别计算介数和改进加权介数，并分别进行排序，比较二者的不同（见表1）。

①大部分介数和改进加权介数的排序基本不变，符合介数是影响结构脆弱性指标的主要因素；

② 序号3、6、12、13、14的改进加权介数与介数的排序变化较大；其中序号3、6带负载相对较大，负载的经济因子也较大，改进加权介数的排名相对靠前了；序号12、13、14带负载相对较小，序号14的经济因子很小，改进加权介数的排名相对靠后。充分说明了负载及其经济因子在结构脆弱性评估中的修正作用。

2）分别计算各输电线路故障后的结构脆弱性指标和状态脆弱性指标，并结合各输电线路故障发生概率计算各输电线路的综合脆弱性指标；分别对各输电线路的结构脆弱性指标、状态脆弱性指标和综合脆弱性指标进行排序和对比（见表2）。

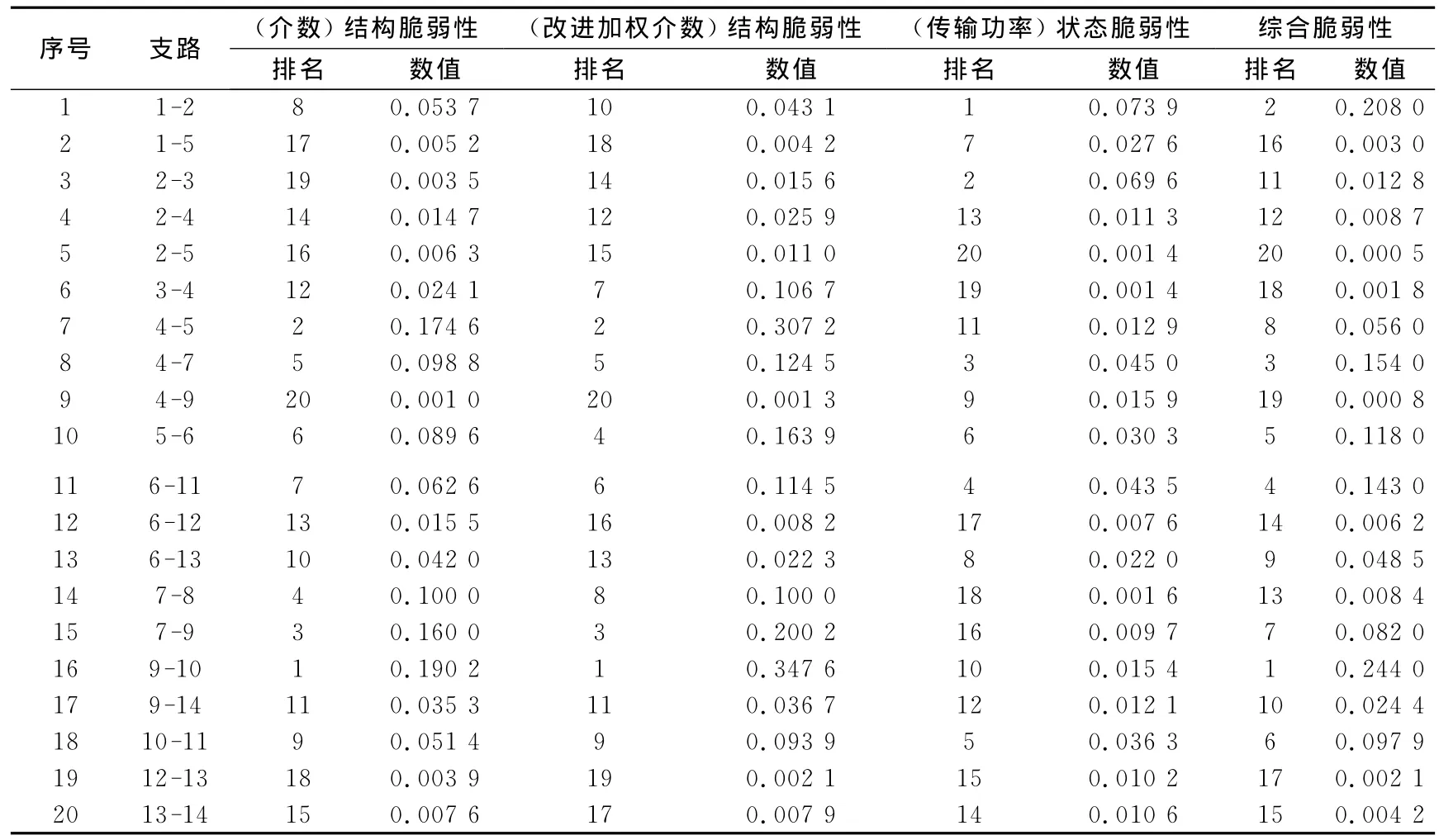
表2 IEEE14节点系统排序结果Tab.2 Indices comparison taxis to IEEE 14bus system

① 编号4、5、8、10、11、16、17的结构脆弱性指标、状态脆弱性指标及综合脆弱性指标的排名基本相同，说明了三个指标具有相似性。

② 编 号 为 1、2、3、6、7、9、13、14、15、18、19、20的综合脆弱性指标的排名是综合了结构脆弱性和状态脆弱性两个指标的综合排序，结果表明结构脆弱性指标和状态脆弱性指标具有互补性，综合脆弱性指标是对两个指标综合考虑的结果。

③考虑线路12的故障发生概率比较低的因素后，综合脆弱性指标排名比只考虑结构或状态的脆弱值有所下降，表明故障发生概率也是影响输电线路脆弱性评估的一个重要因素。

④本文提出的评估方法综合考虑了系统线路故障发生概率以及事故后系统的结构脆弱性指标和状态脆弱性指标，评估结果全面、直观。

3）为进一步说明所提方法的有效性，本文将此方法与V－Q灵敏度进行了比较和分析，对比结果如表3所示。

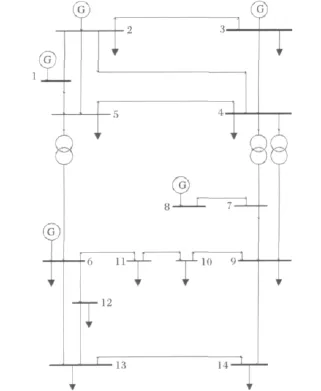
图1 IEEE14节点系统结构图Fig.1 Structure chart of IEEE 14bus system

表3 IEEE14节点系统排序结果对比Tab.3 Indices comparison taxis to IEEE 14bus system

对比第二、三列数据，其中节点4、7、9、14排序有很大变化。由图1分析可知，节点4作为发电机与负荷节点间的主要连接节点之一，担当电力网络中电能传输的主要任务，该节点一旦发生故障对电网影响巨大，所以该节点在考虑结构和状态两方面因素后的脆弱值较V－Q灵敏度分析法有较大提升；节点7是PV节点8接入网络的唯一路径，在电网结构方面影响比较重要，综合评估后脆弱值也有所提升；节点9作为网络连接节点，发生故障后其负荷可以通过其他途径供给，所以节点9脆弱性排序下降；节点14作为电网的远端负荷，该点退出运行后对电网的结构脆弱性和状态脆弱性的影响都不大，进而脆弱性指标的排序也有所下降。

4 结论

本文在文献［14］的基础上引入故障发生概率，并对结构脆弱性评估指标和状态脆弱性评估指标分别进行了改进。

1）定义了电网加权冗余度和经济加权因子两个概念，并提出利用经济因子加权介数对电网加权冗余度进行修正的方法对电网结构脆弱性进行评估，进一步细化各输电线路的结构脆弱性指标。

2）综合考虑节点电压和线路潮流进行电网状态脆弱性评估，从电网局部角度更全面地评估了各输电线路的状态脆弱性。

3）在运用风险理论方法的基础上结合结构脆弱性指标、状态脆弱性指标和故障发生概率求出综合脆弱性指标。这种方法能较好辨识那些故障发生较频繁但后果又较小的故障线路，值得研究。

［1］ 曹一家，刘美君，丁理杰，等（Cao Yijia，Liu Meijun，Ding Lijie，etal）.大电网安全性评估的系统复杂性理论研究（Research on system complexity theory for security evaluation of large power grids）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2007，19（1）：1－8.

［2］ Fouad A A，Zhou Qin，Vitta1V.System vulnerability as a concept to assess power system dynamic security［J］.IEEE Trans on Power Systems，1994，9（2）：1009－1015.

［3］ 卢锦玲，姬群星，朱永利（Liu Jinling，Ji Qunxing，Zhu Yongli）.基于能量函数法的电网脆弱性评估（Power grid vulnerability assessment based on energy function）［J］.电网技术（Power System Technology），2008，32（7）：30－33，45.

［4］ Zhou Qin，Davidson Jennifer，Fouad A A.Application of artificial neural networks in power system security and vulnerability assessment［J］.IEEE Trans on Power Systems，1994，9（1）：525－532.

［5］ 陈 为 化，江 全 元，曹 一 家 （Chen Weihua，Jiang Quanyuan，Cao Yijia）.基于风险理论和模糊推理的电压脆弱性评估（Voltage vulnerability assessment based on risk theory and fuzzy reasoning）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（24）：20－25.

［6］ 陈为化，江全元，曹一家，等（Chen Weihua，Jiang Quanyuan，Cao Yijia，etal）.基于模型组合与风险理论的HVDC系统脆弱性评估（HVDC system vulnerability assessment based on models combination and risk theory）［J］.电力系统自动化（Automation of Electric Power Systems），2005，29（21）：19－24.

［7］ 刘新东，江全元，曹一家，等（Liu Xindong，Jiang Quanyuan，Cao Yijia，et al）.基于风险理论和模糊推理的电力系统暂态安全风险评估（Transient security risk assessment of power system based on risk theory and fuzzy reasoning）［J］.电力自动化设备（E－lectric Power Automation Equipment），2009，29（2）：15－20.

［8］ 王先培，朱天清，熊平（Wang Xianpei，Zhu Tianqing，Xiong Ping）.基于 MAS的电力系统脆弱性评估与控制（Vulnerability assessment and control based on MAS in power system）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2003，15（3）：20－22，27.

［9］ 陈晓刚，孙可，曹一家，等（Chen Xiaogang，Sun Ke，Cao Yijia，et al）.基于复杂网络理论的大电网结构脆弱性分析（Structural vulnerability analysis of large power grid based on complex network theory）［J］.电工技术学报（Transactions of China Electrotechnical Society），2007，22（10）：138－144.

［10］ 倪向萍，梅生伟，张雪敏（Ni Xiangping，Mei Shengwei，Zhang Xuemin）.基于复杂网络理论的输电线路脆弱度评估方法（Transmission lines＇vulnerability assessment based on complex network theory）［J］.电力系统自动化（Automation of Electric Power Systems），2008，32（4）：1－5.

［11］ 丁剑，白晓民，赵伟，等（Ding Jian，Bai Xiaomin，Zhao Wei，et al）.基于二维平面拟合的电网脆弱性分析 （Grid vulnerability analysis based on two－dimensional accumulation means）［J］.电力系统自动化（Automation of Electric Power Systems），2008，32（8）：1－4.

［12］ 威震波，刘俊勇，朱国俊，等（Wei Zhenbo，Liu Junyong，Zhu Guojun，et al）.基于电网状态与结构的综合脆弱评估模型（A new integrative vulnerability evaluation model to power grid based on running state and structure）［J］.电力系统自动化（Automation of Electric Power Systems），2009，33（8）：11－14，55.

［13］ 张健，刘怀东（Zhang Jian，Liu Huaidong）.输电线路概率安全性测度研究（The study of power system dynamic security measure considering the probability of line fault position and transition resistance）［J］.电力系统及其自动化学报（Proceedings of the CSUEPSA），2003，15（6）：34－36.

［14］李生虎，丁明，吴红斌，等（Li Shenghu，Ding Ming，Wu Hongbin，et al）.基于安全性的互联电网间最大输电容量的研究（Research of total transfer capability among power systems considering security）［J］.电力系统及其自动化学报（Proceedings of the CSU－EPSA），2003，15（5）：1－4，38.

［15］ 曹一家，陈晓刚，孙可（Cao Yijia，Chen Xiaogang，Sun Ke）.基于复杂网络理论的大型电力系统脆弱线路辨识（Identification of vulnerable lines in power grid based on complex network theory）［J］.电力自动化设 备 （Electric Power Automation Equipment），2006，26（12）：1－5，31.

［16］Hua Wan，McCalley J D，Vittal V.Risk based voltage security assessment［J］.IEEE Trans on Power Systems，2000，15（4）：1247－1254.

［17］ Tae－Kyun Kim，Jin－Bu Choo，Seung－Hyuk Lee，et al.Security assessment for bus voltages using probabilistic load flow［C］／／International Conference on Probabilistic Methods Applied to Power Systems，A－mes USA：2004.

［18］ 李华强，刘亚梅，Yorino N（Li Huaqiang，Liu Yamei，Yorino N）.鞍结分岔与极限诱导分岔的电压稳定性评估（Voltage stability assessment for saddle node bifurcation and limit induced bifurcation）［J］.中国电机工程学报（Proceedings of the CSEE），2005，25（24）：56－60.

［19］ 刘群英，刘俊勇，刘起方（Liu Qunying，Liu Junyong，Liu Qifang）.运用启发式能量函数观点的无功裕度估算（Reactive power margin estimation by the view of the heuristic energy function）［J］.中国电机工程学报（Proceedings of the CSEE），2008，28（4）：29－36.